Важное значение для народного хозяйства имеет режим региональных сезонных колебаний температур, который можно исследовать с использованием временных рядов многолетних наблюдений. Исследованию временных рядов различной природы посвящено много работ [1–4].
Следуя методике, изложенной в [5], в настоящей работе проведено исследование сезонных значений температур в горной зоне Дагестана (г. Ахты), с использованием данных до 2011 г. В отличие от метода, изложенного в работе [5], в ней проведено усовершенствование метода, включены дополнительные критерии для построения адекватных моделей.
Сначала проводится предварительный статистический анализ данных, результаты которых приведены табл. 1.
Таблица 1
Описательные статистики сезонных температур
|
N |
Сред. |
Мин. |
Макс. |
Дисп. |
Стд. отк. |
Ст. ош. |
Асим. |
Эксц. |
|
|
Зима |
51 |
– 1,33 |
– 13,6 |
11,13 |
20,75 |
4,555 |
0,64 |
– 0,13 |
0,98 |
|
Весна |
51 |
8,79 |
6,67 |
12,13 |
1,34 |
1,159 |
0,16 |
0,68 |
0,38 |
|
Лето |
51 |
19,0 |
17,5 |
21,70 |
0,91 |
0,955 |
0,13 |
0,50 |
0,15 |
|
Осень |
51 |
10,0 |
5,47 |
12,60 |
1,65 |
1,286 |
0,18 |
– 0,89 |
2,26 |
Из данных табл. 1 следует, что наблюдается значительный размах температуры, особенно в зимний период, достигая более 24 градусов. Асимметрия отрицательна в зимний и осенний периоды и положительна в весенний и летний периоды. Осенью наблюдается значительный положительный эксцесс. Все это, в первую очередь, свидетельствует о наличии сложного тренда, и требуются более глубокие исследования для решения данной задачи.
Исследование тенденции изменения среднего значения последних членов ряда по сравнению с климатической нормой проведено с использованием критериев Крамера-Уэлча и Т-критерия Стьюдента. Результаты таких исследований приведены в табл. 2.
Таблица 2
T-критерий независимых выборок и критерий Крамера-Уэлча
|
Сред. |
Сред. |
t-знач. |
ст.с. |
p |
N1 |
N2. |
Ст.от. |
Ст.от. |
F-отн. |
p |
Крам-У |
|
|
Зима |
– 1,82 |
– 0,63 |
– 0,92 |
49 |
0,36 |
30 |
21 |
4,99 |
3,85 |
1,68 |
0,23 |
0,21 |
|
Весна |
8,72 |
8,89 |
– 0,53 |
49 |
0,60 |
30 |
21 |
1,18 |
1,15 |
1,07 |
0,90 |
0,44 |
|
Лето |
18,7 |
19,43 |
– 2,88 |
49 |
0,006 |
30 |
21 |
0,77 |
1,04 |
1,82 |
0,13 |
2,788 |
|
Осень |
9,83 |
10,3 |
– 1,28 |
49 |
0,21 |
30 |
21 |
1,28 |
1,28 |
1,00 |
0,98 |
1,012 |
Из табл. 2 следует, что зимой, весной и осенью рост температуры последних членов ряда незначительный, к тому же дисперсии в эти периоды значительны, достигая 2,2 зимой, и наблюдаемая тенденция роста может быть объяснена случайными факторами, а летом наблюдается тенденция роста температуры. Таким образом, среднее значение температуры в современный период больше климатической нормы (базовый период 1961–1990 гг.) только летом, как по Крамеру-Уэлчу (sig. = 2,78 > 1,96), так и по Т-тесту (sig. = 0,00596 < 0,05), на уровне значимости р = 0,05, в остальные сезоны года, хотя и наблюдается тенденция роста, она может быть объяснена случайностью изменений ряда.
Предварительный анализ показывает, что временной ряд температур в различные сезоны можно рассматривать как реализацию случайного процесса, состоящую из детерминированной и случайной частей. Тогда, следуя методике [5], для построения моделей динамики температур разлагаем временные ряды на основные составляющие: детерминированную и случайную части.
Так как ряды колеблющиеся, то необходимо детерминированную часть разложить на периодическую часть и полином невысокой степени, т.е. ряд можно описать полигармоническим процессом вида
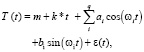 (1)
(1)
где ε(t) – случайная часть с нулевым математическим ожиданием.
Для выделения периодической составляющей используется известное и широко применяемое преобразование Фурье. При этом возникает две взаимосвязанные задачи:
– отделение случайной части от регулярной;
– выделение основных, так называемых, скрытых периодичностей.
Известно, что разложение Фурье выдает все гармоники и для выделения основных необходимо использовать дополнительные условия-критерии.
Сначала, как обычно, строим периодограммы и спектры рядов [1, 2], графики которых приведены на рис. 1 для зимнего (слева) и летнего (справа) сезонов.
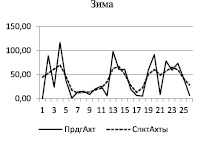
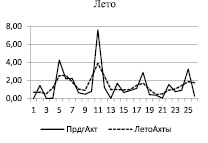
Рис. 1. Периодограммы (сплошная) и спектры (пунктирная) временных рядов
Из периодограмм видно, что они содержат много пиков, а спектры (построены с использованием спектрального окна Хемминга) – относительно небольшое число – 4–6 максимумов, в областях которых осуществляется поиск значимых гармоник.
Для отделения регулярной части от случайной в работе используются следующие критерии случайности остатка ряда: Дарбина-Уотсона, числа поворотных точек, автокорреляционные функции (АКФ), коэффициенты корреляции Пирсона.
Известно, что для оценки степени корреляции остатка ряда используется статистика Дарбина-Уотсона, определяемая по формуле
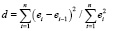 , (2)
, (2)
где ei – остаток ряда.
Составлены соответствующие программы на языке высокого уровня (VBasic), и проведены расчеты. Используя различные критерии случайности, проведен анализ остатка ряда, последовательно включая в циклический тренд пробные гармоники, полученные по результатам спектрального анализа.
Одним из критериев адекватности модели является невязка, определяемая по формуле
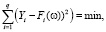 (3)
(3)
где Yi, Fi – фактические и модельные значения ряда, соответственно.
В качестве примера, результаты такого анализа, по данным наблюдений Дагестана (г. Ахты), для зимней температуры приведены в табл. 3.
Таблица 3
Значения критериев случайностей остатка ряда зимнего сезона
|
Периоды (лет) |
Критерий Дарбина-Уотсона |
Число поворотных точек |
Коэффициенты корр. Пирсона |
|||||
|
Невяз ( °С) |
Фкт-Пргн |
Дек-Пргн |
4253Н-Прг |
|||||
|
факт |
теор |
факт |
теор |
|||||
|
16,7, 4,2, 2,6, 2,4 |
2,05 |
2 |
32 |
32 |
646 |
0,61 |
0,11 |
0,15 |
|
16,7, 4,2, 2,6 |
2,31 |
– |
33 |
– |
725 |
0,54 |
0,12 |
0,16 |
|
16,7, 4,2, |
2,24 |
– |
33 |
– |
1019 |
0,23 |
0,11 |
0,16 |
|
16,7, 2,6, 2,4 |
2,29 |
– |
35 |
– |
821 |
0,45 |
0,15 |
0,16 |
|
16,7, 4,2, 2,4 |
2,13 |
– |
31 |
– |
729 |
0,54 |
0,12 |
0,17 |
Из данных табл. 3 следует, что невязка значительная в зимний сезон, потому что размах амплитуды значений больше, чем в остальные сезоны. Нетрудно заметить, что по комплексу параметров наиболее подходит вариант 2 (2 строка), так как большинство критериев соответствует теоретическим значениям, немного уступая по некоторым критериям 1-му варианту (1 строка). Однако вариант 2 лучше по значениям АКФ (рис. 2) и коэффициентам корреляции Пирсона (два последних столбца таблицы), кроме того, периоды 2,6 и 2,4 практически одинаковы, и если 2,4 вносит малый вклад, то выбирается 2-й вариант с периодами: 16,7, 4,2, 2,6 года.
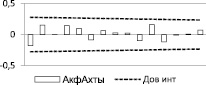
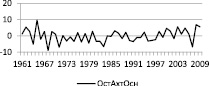
Рис. 2. АКФ остатков ряда (слева) и остатков ряда (справа)
На рис. 2 приведены некоторые результаты такого анализа.
Видно, что АКФ остатка ряда, полученного как разность фактических и модельных значений выбранного варианта, удовлетворяет условию случайности на уровне р = 0,05. По графику остатков ряда (справа) определяется число поворотных точек, теоретическое значение которого определяется по формуле [3]:
N = 2/3(n – 2). (4)
Для оценки степени адекватности построенной модели также проводится анализ регулярной части, для этого используются коэффициенты корреляции Пирсона и результаты широко известных методов сглаживания временных рядов: метода классической декомпозиции и метода основанного на использовании фильтра Ф4253Н [2].
Такой комплексный анализ случайной и регулярной частей ряда, на наш взгляд, может позволить получить более адекватную модель. Использование только минимума невязки также недостаточно, так как минимум, как правило, обеспечивается при наибольшем числе гармоник, а в пределе – всех гармоник, что превращает задачу экстраполяции в задачу интерполяции. На рис. 3 приведены результаты такого анализа.
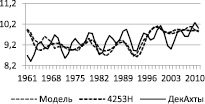
Рис. 3. Результаты модельных вычислений (сплошная) и метода декомпозиции (пунктирная)
Из рисунка видно, что кривые модели и классической декомпозиции хорошо согласуются, это также подтверждают коэффициенты корреляции Пирсона (табл. 2), при этом модельные значения более точно отображают особенности фактических значений ряда, а метод декомпозиции (кстати, и фильтра Ф4253Н) дает слишком сглаженные значения.
После такого комплексного анализа проводится окончательный выбор гармоник и построение моделей. Результаты полученных значений параметров моделей для всех сезонов года приведены в табл. 4.
Таблица 4
Параметры моделей температуры в различные сезоны года
|
Зима |
Весна |
||||||||
|
Коэфф. лин. тр. |
Коэфф. Фурье |
Коэфф. лин. тр. |
Коэфф. Фурье |
||||||
|
m |
k |
период |
кос |
син |
m |
k |
период |
кос |
син |
|
– 0,12 |
2,11 |
0,29 |
– 0,14 |
||||||
|
– 1,93 |
0,02 |
16,7, 4,2, 2,6 |
0,42 |
1,95 |
8,7 |
0,005 |
16,7, 5,6, 3,1 |
0,55 |
0,05 |
|
– 1,51 |
– 0,99 |
0,44 |
– 0,16 |
||||||
|
лето |
Осень |
||||||||
|
0,27 |
– 0,019 |
0,58 |
– 0,01 |
||||||
|
18,3 |
0,03 |
50, 12,5, 5,0 |
0,43 |
0,10 |
9,70 |
0,01 |
50, 6,3, 3,8 |
– 0,06 |
– 0,58 |
|
0,51 |
– 0,28 |
– 0,11 |
– 0,45 |
||||||
Используя данные таблицы, легко построить модели для всех сезонов, для этого достаточно из таблицы подставить в формулу (1) соответствующие коэффициенты Фурье и линейного тренда. Так, например, для зимнего сезона построена модель вида
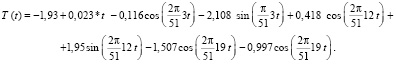
На рис. 4 приведены графики фактических и прогнозных значений температуры зимнего сезона по построенной модели, до 2040 года.
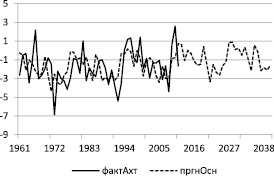
Рис. 4. Фактические (сплошная) и прогнозные (пунктирная) значения ряда
Из графиков рисунка следует, что в годы наблюдений кривые хорошо согласуются, что свидетельствует об адекватности построенной модели. Значения температуры изменяются достаточно сложным образом, совершая колебания около линейного тренда, указывающего на слабую тенденцию роста. Максимальные значения она принимает в годы 2014–2018 и 2030–2035 годы, а минимальные – в 2022–2028 годы.



