Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Естественной трансверсальной изотропией упругих свойств обладают кристаллы гексагональной сингонии. Кроме того, однородные изотропные тела с плоскопараллельной системой трещин, а также неоднородные слоистые геологические среды при выполнении ряда условий заменяют так называемыми эффективными анизотропными моделями. В контактных задачах для деформируемых анизотропных сред нужно оценивать особенности волновых фронтов. В целом задача построения фронтов является тривиальной лишь для изотропных однородных сред. В случае же реальных сред (например, геосред) построение фронтов сопряжено с рядом вычислительных особенностей.

Фундаментальные основы для решения задач кристаллоакустики заложены во второй половине нашего столетия Ф.И. Федоровым [1]. Удается получать и исследовать общее решение уравнений эластодинамики для широкого класса практических случаев. Эти результаты находят свое применение в физической акустике, дефектоскопии, пьезотехнике, сейсморазведке. При этом для многих задач возможно лишь численное решение, но для правильной интерпретации результатов расчетов необходимо опираться на некие общие аналитические зависимости. Авторами ниже рассмотрены несколько характерных случаев гексагональной сингонии и построены индикатрисы лучевых скоростей. При несовпадении оси нагружения с главной осью анизотропии результат получен конечно-разностным моделированием.

Тензор Кристоффеля. В трансверсально изотропных средах наибольшая анизотропия упругих свойств наблюдается в плоскости (010). Распространение упругих волн будем рассматривать в этой плоскости. Совместим орты кристаллографической системы координат с осями X, Z. Будем считать, что среда находится в условиях плоской деформации. Запишем уравнения движения в перемещениях

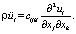(1)

Уравнения (1) являются линейными однородными дифференциальными уравнениями второго порядка относительно вектора смещения [2].

Решение уравнений (1) представляет собой семейство плоских волн

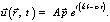(2)

Здесь 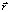– радиус-вектор частицы среды, А – амплитуда волн, 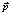– вектор поляризации, 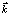– волновой вектор (вектор пространственных частот), 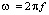– круговая частота, где f – частота (число полных колебаний вектора смещения за одну секунду). Единичный вектор волновой нормали 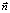, такой, что 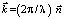, где λ – длина волны, в оптике называется вектором рефракции (медленность или обратная скорость). Возмущение частоты f в среде пробегает путь λ за время 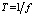, а величину 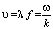называют фазовой скоростью, где k – длина вектора .

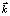Выражение (2) для вектора смещения плоской упругой волны является комплексным, тогда как реальные смещения должны выражаться вещественными величинами. Разрешение этого противоречия заключается в том, что уравнения (1) являются линейными однородными уравнениями, причем все операции, производимые над неизвестным вектором, не содержат мнимых выражений [2].

Учитывая вышесказанное, равенство (2) запишем в виде

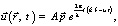(3)

подставляя (3) в уравнения (1), получим

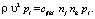(4)

Здесь nj, nk – направляющие косинусы вектора волновой нормали, а свертка cijkl nj nk есть тензор второго ранга – тензор Кристоффеля Гil. Введем вместо тензора cijkl тензор 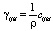, который называется приведенным тензором модулей упругости. Тогда свертка ijkl nj nk есть приведенный тензор Кристоффеля 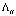. Перепишем уравнение (4) в виде

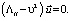(5)

Векторное уравнение (5) есть уравнение Кристоффеля. Оно является основным для всей теории упругих волн в кристаллах. Собственными значениями приведенного тензора Кристоффеля 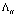являются квадраты фазовых скоростей, а его собственным вектором – вектор поляризации 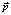. При вычислении компонент тензора Кристоффеля нужно учитывать, что, например, c2323 = c2332 = c3232 = c3223 = c44.

В плоскости (010) матрица приведенного тензора Кристоффеля будет иметь вид

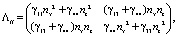
где индекс 4 соответствует сочетаниям индексов (13) и (31).

Характеристическое уравнение матрицы тензора Кристоффеля

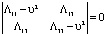
имеет корни

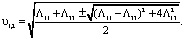(6)

Трансверсально изотропная среда (в частности, гексагональные кристаллы) является единственным примером анизотропной среды, для которой уравнение Кристоффеля при любом направлении волновой нормали распадается на линейное и квадратное уравнения и поэтому допускает сравнительно простое решение [2]. Поскольку такие среды в отношении упругих свойств обладают симметрией вращения вокруг оси 6-го порядка, то все волновые поверхности будут поверхностями вращения. Чтобы их получить, достаточно найти вид соответствующей кривой в меридиональной плоскости (плоскости симметрии, проходящей через ось 6-го порядка), после чего вращение кривой вокруг оси 6-го порядка даст искомую поверхность.

Результаты исследования и их обсуждение

Индикатрисы фазовых скоростей υ1,2 и медленностей 1/υ1,2 легко строятся непосредственно по формулам (6). Для построения волновых (лучевых) поверхностей нами использован геометрический метод Postma [8]. Для иллюстрации характера этих кривых выберем гексагональные кристаллы с различной степенью анизотропии.

В таблице приведены константы для ряда гексагональных кристаллов (компоненты cij даны в ГПа, плотность – в кг/м3). Данные расположены по возрастанию плотности монокристаллов от разновидности Ih пресного льда до карбида вольфрама WC. Даны ссылки на работы, из которых были взяты константы. Далее, кроме обычно используемых упругих модулей и плотности в таблице приводятся так называемые безразмерные эффективные параметры анизотропии [9]:

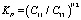– характеризует анизотропию по скорости квази-P–волн;

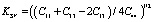– характеризует анизотропию по скорости квази-SV-волн.

Эти параметры удобны при моделировании в плоскости (010), так как для изотропной среды .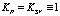

Из таблицы выбраны три характерных среды: 1 – стабильная разновидность пресного льда Ih, 2 – цинк (Zn), 3 – стабильный графит (α–C).

На рис. 1 построены кривые фазовых скоростей (а), обратных скоростей (б) и лучевых скоростей (в) для льда, на рис. 2, a, б, в – для цинка, и на рис. 3, a, б, в – для графита, одного из предельных случаев анизотропии. В изотропной среде кривые (индикатрисы) для всех скоростей были бы концентрическими окружностями, а поверхности фазовых скоростей, медленностей и лучевых скоростей в пространственном случае – сферами.

Рис. 1. Индикатрисы медленностей (а), фазовых скоростей (б) и лучевых скоростей (в) монокристалла пресного льда Ih. Черная линия – квазипродольная волна, серая – квазипоперечная волна

Рис. 3. Индикатрисы медленностей (а), фазовых скоростей (б) и лучевых скоростей (в) монокристалла графита. Черная линия – квазипродольная волна, серая – квазипоперечная волна

Показанные на рисунках кривые есть сечения поверхностей – поверхности медленностей (слева), фазовых скоростей (в центре) и поверхности лучевых скоростей (справа). Последние поверхности есть не что иное, как фронты распространяющихся волн, ибо энергия в волне переносится по лучам. Участки вогнутости поверхностей медленностей определяют области неоднозначности на фронтах. В изотропной среде лучевые и фазовые скорости совпадают – фронты (волновые поверхности) представляют собой сферы, и нормаль в любой точке фронта коллинеарна лучу, проведенному к этой точке из места излучения.

По индикатрисам льда заметна слабая анизотропия, и областей неоднозначности не видно. Зато для монокристалла цинка хорошо видна выраженная анизотропия по продольной скорости (латеральная вытянутость, квази-эллиптичность внешней кривой рис. 2, в). Внутренняя кривая, соответствующая индикатрисе квазипоперечной скорости, обладает характерными признаками сильной анизотропии – зонами рефракции, так называемыми «петлями» на лучах ± π/2.

Рис. 2. Индикатрисы медленностей (а), фазовых скоростей (б) и лучевых скоростей (в) монокристалла цинка. Черная линия – квазипродольная волна, серая – квазипоперечная волна

Монокристалл графита является граничным случаем анизотропии в том смысле, что для него, во-первых, характерны максимальные отклонения луча от волновой нормали (ромбовидный фронт), и, во-вторых, для широкого диапазона лучей скорость одной из ветвей квазипоперечной волны практически равна скорости квазипродольной волны – индикатрисы касаются друг друга.

Для случая несовпадения главной оси анизотропии и оси нагружения было решено использовать численный метод расчета полного волнового поля, основанный на конечно-разностном моделировании [1]. Приведем для сравнения волновую картину в задаче Лэмба для монокристалла цинка конечных размеров в случае, когда ось нагружения коллинеарна оси С (рис. 4) и для случая, когда угол между ними составляет 30 ° (рис. 5).

Рис. 4. Волновые фронты в монокристалле цинка в случае коллинеарности осей анизотропии и нагружения для двух моментов времени. Буквами обозначены: P – квазипродольная волна, SV – квазипоперечная волна, LR – волна Рэлея, C – коническая волна

Рис. 5. Волновые фронты в монокристалле цинка для случая угла 30 градусов между осью нагружения (черная стрелка) и осью анизотропии (линия). Буквой R обозначена отраженная от свободной поверхности продольная волна

Каждая из волновых картин на рис. 4–5 представляет собой мгновенные снимки (скриншоты) волнового поля для двух моментов времени. Вид фронта продольной и поперечной волн на рис. 4 соответствует индикатрисам рис. 2, в. Хорошо различимы петли для квази-SV волн, на скриншоте они воспринимаются как отдельные ветви фронта. Для более раннего момента фронт продольной волны еще не достиг нижней грани, для более позднего начинается отражение. Это показано на рис. 5, б: фронт продольной волны, достигнув нижней грани (на ней задано условие свободной поверхности), начинает отражаться от неё, фронт отраженной волны отмечен буквой R.

Выводы

Изложенная методология может быть использована в сейсморазведке при построении временных сейсмических разрезов и при оценке особенностей распространения сейсмических волн в горизонтально-слоистой среде. Кроме того, методы построения волновых фронтов могут применяться на стадии планирования и обработки результатов лабораторного моделирования в материаловедении, кристаллофизике и дефектоскопии.