Исследованию изменений климата в настоящее время уделено много внимания. Наиболее часто говорят о его глобальном потеплении, хотя существует и противоположная точка зрения, утверждающая о возможном похолодании. Само существование двух противоположных мнений об изменении климата недвусмысленно говорит, что эта проблема далека от завершения и необходимы дальнейшие исследования этой сложной проблемы, используя различные методы. Необходимость исследования этой проблемы также отмечена МГЭИК, при этом использованы результаты региональных наблюдений за динамикой основных климатических характеристик – основных метеорологических параметров. В частности, проводятся исследования динамики температуры, количества осадков, влажности и других основных характеристик климата, используя данные многолетних наблюдений. Анализу временных рядов различной природы посвящено много работ [1–4]. В настоящей работе, используя данные метеорологических параметров за более чем полувековой период наблюдений, проводятся исследования данных пунктов Северного Кавказа по данным наблюдений (Ставропольского края, КБР, КЧР, Дагестана) и Крыма, и их сравнительный анализ.
Сначала проведен предварительный статистический анализ данных. В табл. 1 приведены результаты такого анализа для среднегодовой температуры воздуха.
Таблица 1
Описательная статистика среднегодовой температуры воздуха
|
Пункты |
N |
Ср. |
Мин |
Макс |
Дисп |
Вар |
Асим |
Эксц |
Кр-У |
|
Каменомост |
55 |
7,55 |
6,100 |
9,300 |
0,577 |
3,2 |
0,256 |
– 0,374 |
– 1,5 |
|
Нальчик |
68 |
9,52 |
7,600 |
11,60 |
0,946 |
1,92 |
– 0,022 |
– 0,733 |
– 4,2 |
|
Прохладный |
55 |
10,4 |
8,516 |
12,00 |
0,797 |
3,48 |
– 0,167 |
– 0,860 |
– 3,5 |
|
Кисловодск |
51 |
7,97 |
6,200 |
10,60 |
0,703 |
4,4 |
0,534 |
1,163 |
– 1,3 |
|
Ставрополь |
51 |
9,51 |
7,40 |
11,70 |
0,93 |
4,3 |
0,007 |
– 0,284 |
– 2,1 |
|
Арзгир |
45 |
10,6 |
8,400 |
12,40 |
0,918 |
4,0 |
– 0,177 |
– 0,93 |
– 0,2 |
|
Ахты |
51 |
9,39 |
7,700 |
11,60 |
0,611 |
3,9 |
0,267 |
0,58 |
– 2,6 |
|
Теберда |
51 |
6,71 |
5,30 |
9,30 |
0,59 |
4,0 |
0,68 |
1,47 |
– 3,3 |
|
Симферополь |
67 |
10,9 |
8,74 |
13,1 |
0,77 |
4,36 |
– 0,32 |
0,26 |
– 2,9 |
В таблице приведены данные среднегодовой температуры по Северному Кавказу по всем трем зонам: горной, предгорной и степной (равнинной) и данные по Крыму по станции Симферополь.
В четырех горных районах Северного Кавказа (Каменомост, Кисловодск, Теберда, Ахты с высотами над уровнем моря от 800 до более чем 1300 м средние годовые значения температуры за периоды наблюдений принимают от 6,71 до 9,39 градусов, минимальные и максимальные значения от 5,3 до 11,6, т.е. размах достигает 6,3 градуса. Максимальная асимметрия равна 0,68, а эксцесса, достигает – 1,47.
В двух предгорных районах Северного Кавказа (г. Нальчик (500 н.у.м., г. Ставрополь (540 н.у.м.) средние годовые значения температуры за периоды наблюдений принимают соответственно 9,52 до 9,51 градуса, минимальные и максимальные значения от 7,6 до 11,6, т.е. размах достигает 4 градусов, а Ставрополя соответственно от 7,4 до 11,7 – размах 4,3 градуса. Асимметрия отрицательна и равна – 0,022, а Ставрополя 0,007, а эксцесса (Нальчик) достигает – 0,733, а Ставрополя – 0,284.
Аналогично ведут себя и данные по степным зонам КБР и Ставрополя (по пунктам г. Прохладный (200 м н.у.м.) и Арзгир (200 м н.у.м.)) Средние значения (Прохладный) – 10,4, Арзгир – 10,6, минимальные – 8,52 и 8,4 – максимальные – 12 и 12,4 соответственно.
По данным Симферополя среднее значение выше остальных пунктов и равно 10,9, минимальное – 8,74, а максимальное равно 13,1, асимметрия отрицательна и равна – 0,32, эксцесс положителен и равен 0,26.
Во всех пунктах наблюдается некоторое повышение среднегодовой температуры за последние десятилетия, по сравнению с климатическими нормами.
Из последнего столбца таблицы следует, что в пунктах Каменомост, Кисловодск и Арзгир наблюдаемая тенденция роста температуры может быть объяснена случайностью изменений рядов, так как значения критерия Крамера – Уэлча меньше критического, т.е. |sig| < 1,96, в остальных пунктах тенденция роста температуры значима на уровне р = 0,05.
Сравнение среднегодовых значений температуры Северо-Кавказских регионов с данными Крыма показывает, что наиболее близкие значения наблюдаются с данными Ставропольского края (г. Аргзир) и КБР (г. Прохладный). Наименьшие и наибольшие вариации среднегодовой температуры на Северном Кавказе приходятся на пункты наблюдений: г. Нальчик (1,92) и г. Кисловодск (4,4).
Во всех горных пунктах наблюдается некоторое повышение среднегодовой температуры за последние десятилетия по сравнению с климатическими нормами. Так, например, в пункте г. Теберда наблюдается повышение температуры на 0,57 градуса, а в пункте г. Ахты – на 0,45 градуса.
Аналогичные исследования проведены в предгорной и степной зонах. Из результатов, приведенных в таблице, видно, что в предгорной зоне наблюдается некоторое повышение среднегодовой температуры за последние десятилетия по сравнению с климатическими нормами. Так, например, в пункте г. Нальчик наблюдается повышение температуры на 0,89 градуса, а в пункте г. Ставрополь – на 0,55 градуса.
В степной зоне также наблюдается повышение среднегодовой температуры за последние десятилетия по сравнению с климатическими нормами. В частности, в пункте г. Прохладный наблюдается повышение на 0,7 градуса, а в пункте г. Арзгир – на 0,01 градуса.
Такие же исследования проведены по данным Крыма. Повышение среднегодовой температуры за последние десятилетия по сравнению с климатическими нормами (г. Симферополь) наблюдается на 0,48 градуса.
Сравнивая приведенные в таблице значения в предгорной и степной зонах КБР (Нальчик, Прохладный) с данными Симферополя видим, что температура в указанных зонах меняется от 7,6 до 12 градусов, дисперсия изменяется от 0,577 до 0,946, асимметрия от – 0,022 до 0,68, эксцесс от – 0,733 до 1,47, в Симферополе от 8,74 до 13,1, дисперсия – 0,77, асимметрия – 0,32, эксцесс 0,26. Видно, что данные Симферополя по значениям температуры выше, чем в указанных зонах КБР.
Сравнение значений в предгорной и степной зонах Ставропольского края (Ставрополь, Арзгир) с данными Симферополя показывает, что температура в указанных зонах Ставропольского края меняется от 7,4 до 12,4 градуса, дисперсия изменяется от 0,918 до 0,93, асимметрия от – 0,177 до – 0,007, эксцесс от – 0,284 до – 0,93, Отсюда следует, что данные Симферополя по температуре выше, чем в указанных зонах Ставропольского края. Асимметрии отрицательны и практически одинаковы, эксцесс отрицательный и по абсолютной величине значительно больше в Арзгире.
Сравнение значений в горной зоне Дагестана (Ахты, Прикаспийская зона) с данными Симферополя (Причерноморская зона) показывает, что температура в указанной зоне Дагестана меняется от 7,7 до 11,6 градуса, дисперсия 0,611, асимметрия 0,267, эксцесс 0,58. Отсюда видно, что данные Симферополя выше по сравнению с данными Ахты, асимметрия положительна, эксцесс положительный и более чем в два раза превышает значение в Симферополе.
Сравнение значений в горной зоне КЧР (Теберда) с данными Симферополя показывает, что температура в Теберда меняется от 5,3 до 9,3 градуса, дисперсия 0,59, асимметрия положительна и равна 0,68, эксцесс 1,47. Таким образом, данные Симферополя по температуре выше, чем значения в г. Теберда, асимметрия и эксцесс положительные и значительно превышают соответствующие значения в Симферополе.
Таким образом, по данным наблюдений рассмотренных в работе по Северному Кавказу среднегодовая температура максимальна в Ставропольском крае (г. Арзгир – 10,6) и минимальна в Теберда (КЧР – 6,71), а в Крыму – 10,9.
Для сравнения данных наблюдений также приведены графики рассмотренных временных рядов значений температуры. На рис. 1 приведены сравнительные графики данных среднегодовой температуры отдельно по всем зонам и по Крыму.
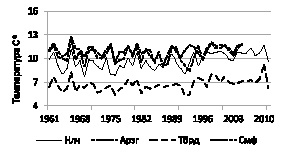
Рис. 1. Графики температур
Из графиков видно, что кривые хорошо коррелируют с высоким коэффициентом корреляции, достигая значения, равного 0,87.
На рис. 1 приведены фактические значения температуры в этих пунктах, из которых видно, что они хорошо коррелируют.
Нетрудно заметить, что кривые, изменяются синхронно, повторяя минимальные и максимальные значения в определенные периоды.
Также можно заметить, что начиная с 1990-х гг. наблюдается заметное повышение в среднем температуры воздуха. Более детальный анализ этого явления проведен с использованием критерия Крамера – Уэлча.
Проведенный выше анализ носит предварительный статистический характер и дает осредненные грубые характеристики. Поэтому, наряду с описательным, проведено более подробное сравнение особенностей изменения температуры, в этих пунктах, предварительно исключив влияние неконтролируемых случайных факторов.
Представляя ряд в виде суммы состоящей из регулярной и случайной части, по предложенной в работе [5] методике, построены модели временных рядов температуры в исследованных пунктах. Проведено разложение рядов на регулярную и случайную части, выделены скрытые периоды и построены модели.
Следуя этой методике, для построения модели динамики температуры, детерминированную часть можно разложить на периодическую часть и полином невысокой степени, т.е. ряд можно описать полигармоническим процессом вида
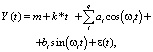
где ε(t) – случайная часть с нулевым математическим ожиданием.
Используя преобразование Фурье, проводится анализ и выделение периодической составляющей.
Важнейшим этапом такого анализа-исследования является выделение скрытых периодичностей с использованием спектрального анализа, результаты которых приведены на следующих рисунках. Сравнение периодограмм в различных пунктах показывает, что по ним сложно провести сравнительный анализ. Поэтому приведены спектры, построенные сглаживанием периодограмм с помощью спектрального окна Хемминга.
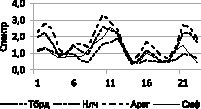
Рис. 2. Спектры температуры
Из рис. 2 видно, что спектры среднегодовой температуры в различных зонах Северного Кавказа (горной (Теберда, сплошная), предгорной (Нальчик, пунктирная), степной (Арзгир, точечная) и Симферополя (штрих-пунктирная) практически идентичны. В них содержатся пять наиболее ярко выраженных областей максимума, которые практически совпадают. В этих областях проводится поиск наиболее значимых (основных) гармоник, с использованием различных критериев случайностей ряда.
При построении моделей поиск основных гармоник проводится в областях максимумов спектров, используя известные критерии случайностей остатка ряда, в частности критерий Дарбина – Уотсона, АКФ, числа поворотных точек (чпт) и другие.
На рис. 3 приведены некоторые результаты такого анализа. В частности одним из основных требований к остатку ряда является отсутствие регулярной части (тренда) в остатке, которое определяется по АКФ остатка ряда. В качестве примера на рис. 3 приведены АКФ остатков рядов для данных г. Теберда и г. Симферополя.
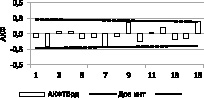
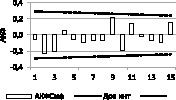
Рис. 3. АКФ остатков рядов температуры
Из графиков АКФ видно, что они удовлетворяют условию случайности на уровне значимости р = 0,05. Аналогично проверяется случайность остатка ряда по вышеперечисленным критериям.
Кроме того регулярная часть сравнивается с известными хорошо зарекомендовавшими себя методами классической декомпозиции и сглаживания ряда с использованием фильтра 4253Н. Исследование многочисленных рядов предлагаемым методом показывает, что такой комплексный анализ случайной и регулярной частей ряда дает более надежные результаты, больше того, неучет анализа регулярной части может привести, и приводит, к ошибочным результатам.
На рис. 4 приведены результаты такого анализа.
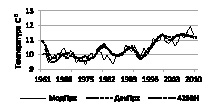
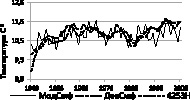
Рис. 4. Модельные, классической декомпозиции и фильтра 4253Н, значения температуры
Из данных рисунка видно, что результаты, полученные по моделям, хорошо согласуются с фактическими. Это дает основание утверждать, что построенные модели адекватно отражают реальные данные и могут быть использованы для сравнительного анализа данных исследуемых территорий. Видно, что методы декомпозиции и фильтра слишком сглаживают, а модельные более точно описывают реальные значения ряда.
В табл. 2 приведены в сравнении параметры моделей среднегодовой температуры и их основные характеристики по данным Северного Кавказа и Крыма.
Таблица 2
Основные параметры моделей
|
Пункты |
Периоды |
Св.чл. |
Угол нак |
Крам-У |
Стьюд |
|
Каменомост |
8,5, 4,6 |
7,18 |
0,012 |
15,67 |
0,000000 |
|
Нальчик |
50, 10, 3 |
8,86 |
0,027 |
26,64 |
0,000000 |
|
Прохладный |
50, 10, 3 |
9,6 |
0,026 |
34,30 |
0,000000 |
|
Кисловодск |
9, 4,1 |
7,87 |
0,0038 |
13,84 |
0,000047 |
|
Ставрополь |
50, 10, 3,8 |
8,84 |
0,016 |
19,23 |
0,000000 |
|
Арзгир |
44, 4, 3 |
10,08 |
0,012 |
10,51 |
0,000003 |
|
Ахты |
10, 5, 3 |
9,031 |
0,014 |
18,67 |
0,000000 |
|
Теберда |
10, 5, 3 |
6,2 |
0,019 |
17,12 |
0,000000 |
|
Симферополь |
44, 4,4, 2,9 |
10,35 |
0,015 |
6,501 |
0,007000 |
Из данных таблицы следует, что основными гармониками являются: низкие (1–2), средние (5–6) и высокие (15–17). Более стабильно встречаются периоды 9–10, 5 лет и 3 года, видимо они ближе к какому-то общему механизму, например к циклам солнечной активности. Незначительные колебания из-за небольших различий длин рядов, которые с их увеличением будут уточняться. Следует также отметить, что низкие гармоники более чувствительны к длине ряда.
Из угловых коэффициентов линейного тренда следует, что наблюдается тенденция роста соответствующая росту температуры около 1–2 градуса на сто лет. Немного выше угловой коэффициент в пунктах (г. Нальчик и г. Прохладный), и наименьшее значение наблюдается в г. Арзгире. Далее проведено исследование статистической значимости наблюдаемых тенденций роста температуры в современный период по сравнению с климатической нормой (1961–1990 гг).
Из табл. 2 видно, что с большой вероятностью, и по критерию Крамера – Уэлча (sig = I >> 1,96), и по Т-тесту Стьюдента (sig = I << 0,05), тенденция роста температуры в современный и прогнозируемый период, значима на уровне р = 0,05 для всех приведенных пунктов наблюдения Северного Кавказа и Крыма.
На рис. 5 в качестве примера, приведены в сравнении прогнозные значения до 2040 г. по данным Симферополя (справа) и пункта Северного Кавказа (г. Теберда) (слева).
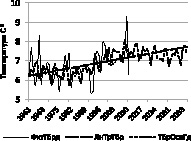
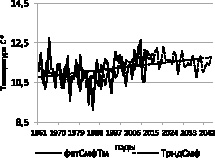
Рис. 5. Фактические и прогнозные значения температур воздуха
Из графиков рисунка видно, что модельные и фактические значения достаточно хорошо согласуются в годы наблюдений, что свидетельствует об адекватности построенных моделей.
Прогнозные значения изменяются в соответствии с построенными моделями, которые свидетельствуют о тенденции роста температуры, совершая циклические колебания. Ожидаемые значения температуры выше тренда в первые 20 лет прогноза, затем наступает некоторое похолодание, и температура идет ниже тренда.
Заключение
Таким образом, проведенный анализ среднегодовой температуры по данным пунктов наблюдения Северного Кавказа и Крыма показал, что динамика температуры носит достаточно сложный колебательный характер. В связи с этим были использованы современные методы анализа временных рядов, которые позволили провести достаточно полный их анализ. Построенные модели подтверждают фактически наблюдаемую тенденцию роста среднегодовой температуры в годы прогноза, на уровне значимости р = 0,05, по критериям Крамера – Уэлча и Стьюдента.
Достоверность полученных результатов подтверждается использованием основных критериев случайностей ряда, а также согласованием полученных результатов с широко используемыми методами сглаживания рядов.



