Результаты изучения взаимодействия рентгеновского и гамма-излучения с веществом находят широкое применение во многих областях техники, медицины, радиационной защиты, создании биологических сенсоров. С этой целью необходимо уметь оценивать эффективный атомный номер сложного по составу вещества, чтобы прогнозировать изменение его характеристик под воздействием облучения фотонами различной энергии.
Целью настоящей работы является получение аналитической зависимости эффективного атомного номера от состава вещества и энергии излучения для широкого диапазона изменения энергии излучения и состава мишени.
Теория. Основные формулы
Массовый коэффициент ослабления излучения многоэлементной мишенью можно записать в виде
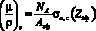 , (1)
, (1)
где эффективный атомный вес
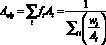 , (2)
, (2)
а атомный коэффициент ослабления
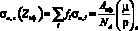 , (3)
, (3)
где 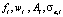 – атомная, весовая концентрация, атомный вес, полный атомный коэффициент ослабления (поперечное сечение) элемента с номером i. NA – число Авогадро.
– атомная, весовая концентрация, атомный вес, полный атомный коэффициент ослабления (поперечное сечение) элемента с номером i. NA – число Авогадро.
В диапазоне энергий Е < 1 МэВ основными процессами взаимодействия рентгеновского и гамма-излучения с атомами вещества являются: фотоэлектронное поглощение, когерентное и некогерентное рассеяние, которые зависят от атомного номера элемента как ~ Z4, ~ Z2, ~ Z соответственно [1, 2]. На рис. 1 показана зависимость отношения коэффициента когерентного рассеяния к полному коэффициенту атомного ослабления по данным XCOM [4].
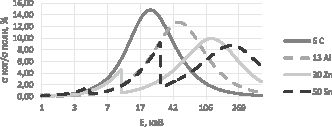
Рис. 1. Зависимость доли когерентного рассеяния в полном атомном сечении ослабления от энергии для элементов с Z = 6, 13, 30, 50
Как видно, с увеличением энергии вклад когерентного рассеяния достигает максимального значения и затем уменьшается. Поэтому целесообразно учитывать только фотоэлектрическое поглощение и некогерентное рассеяние и рассматривать энергии излучения больше энергии краёв поглощения атомов элементов, составляющих пробу. Тогда полный атомный коэффициент ослабления излучения в веществе с атомным номером Z можно представить в виде
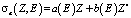 , (4)
, (4)
полагая, что вклад в ослабление излучения когерентным рассеянием частично или полностью будет учтен подбором коэффициентов а(E) и b(E) в формуле (4), где E – энергия излучения.
Для нахождения зависимости (4) достаточно оценить два коэффициента а и b. Это можно сделать по двум значениям 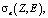 найденным экспериментально либо взятым, например, из XCOM [4]. В данной работе использовался последний способ. На рис. 2 приведены графики зависимости атомных коэффициентов ослабления от атомного номера Z, рассчитанные по формуле (4) с использованием коэффициентов а и b, найденных по двум значениям
найденным экспериментально либо взятым, например, из XCOM [4]. В данной работе использовался последний способ. На рис. 2 приведены графики зависимости атомных коэффициентов ослабления от атомного номера Z, рассчитанные по формуле (4) с использованием коэффициентов а и b, найденных по двум значениям 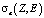 (в качестве опорных элементов использовались Z = 13, 50), взятым из XCOM. Расчеты проведены для энергий излучения в диапазоне 40–140 кэВ.
(в качестве опорных элементов использовались Z = 13, 50), взятым из XCOM. Расчеты проведены для энергий излучения в диапазоне 40–140 кэВ.
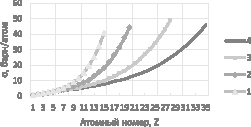
Рис. 2. Зависимость полного атомного коэффициента ослабления от атомного номера Z: 1, 2, 3, 4 соответственно для энергий 40,32; 59,54; 94,52; 136,55 кэВ. Сплошные линии – расчет по формуле (4) с коэффициентами из табл. 1, точки – данные XCOM [4]. σа в барн/атом
В табл. 1 приведены значения а и b, найденные для различных энергий излучения, и относительная среднеквадратичная ошибка аппроксимации Sотн. зависимостью (4) табличных данных полных атомных сечений XCOM.
Таблица 1
Значения коэффициентов а(E), b(E), B(E) и точность аппроксимации Sотн. для 1 ≤ Z ≤ 56
|
E, кэВ |
α |
b*104 |
B*10-4 |
Sотн , % |
|
40,32 |
0,6199 |
5,9452 |
0,10427 |
8,4 |
|
59,54 |
0,5139 |
2,0726 |
0,24793 |
4,1 |
|
94,52 |
0,4837 |
0,5745 |
0,84197 |
1,6 |
|
136,55 |
0,4509 |
0,2042 |
2,20799 |
1,2 |
Из результатов табл. 1 и графиков рис. 2 следует вывод о хорошем согласии расчетов по формуле (4) с данными XCOM в широком диапазоне энергий и атомных номеров 1 < Z < 56–60.
Введем обозначения
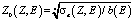 ,
,
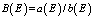 ,
,
тогда далее, из (4), можно получить
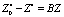 . (5)
. (5)
Воспользуемся следующей оценкой:
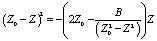 . (6)
. (6)
Величина в скобках правой части должна быть меньше нуля. В этом случае
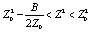 , (7)
, (7)
т.е. Z – решение уравнения (4) – должно находиться в интервале
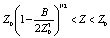 , (8)
, (8)
Упростим выражение (8), тогда приближенное аналитическое решение уравнения (4) будет
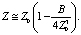 (9)
(9)
На рис. 3 и 4 показаны графики зависимости отклонения 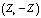 от Z, где в качестве Zr использовалось Z0 (график 1) и
от Z, где в качестве Zr использовалось Z0 (график 1) и 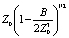 (график 4).
(график 4).
График под номером 2 соответствует расчету Zr по формуле (9), а 3 – расчету по формуле 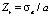 . Z – значение атомного номера элемента, которому соответствует величина полного атомного коэффициента ослабления в формуле (4). В табл. 2 приведены значения абсолютных и относительных среднеквадратических отклонений, максимальное абсолютное отклонение по модулю
. Z – значение атомного номера элемента, которому соответствует величина полного атомного коэффициента ослабления в формуле (4). В табл. 2 приведены значения абсолютных и относительных среднеквадратических отклонений, максимальное абсолютное отклонение по модулю 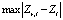 и значение Zi, при котором наблюдается это отклонение. В табл. 2 указаны также значения Zсшивки, при котором согласовывались
и значение Zi, при котором наблюдается это отклонение. В табл. 2 указаны также значения Zсшивки, при котором согласовывались 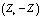 для графиков 2 и 3. Из табл. 2 следует, что комбинация двух зависимостей 2 и 3 обеспечивает абсолютное расхождение результатов, не превышающее единицы во всем диапазоне Z = 1 – 56(60) при энергиях 40–140 кэВ.
для графиков 2 и 3. Из табл. 2 следует, что комбинация двух зависимостей 2 и 3 обеспечивает абсолютное расхождение результатов, не превышающее единицы во всем диапазоне Z = 1 – 56(60) при энергиях 40–140 кэВ.
Таблица 2
Характеристики точности вычисления атомного номера Zr по формуле 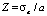 для Z < Zсшивки и по формуле (12) для Z > Zсшивки для энергий в диапазоне 40–140 кэВ
для Z < Zсшивки и по формуле (12) для Z > Zсшивки для энергий в диапазоне 40–140 кэВ
|
E, кэВ |
Sабс |
|
Sотн, % |
Zсшии |
Диапазон Z |
|
40,32 |
0,09 |
0,33;5 |
1,63 |
3 |
56 |
|
59,54 |
0,14 |
0,45;7 |
1,81 |
5 |
1–60 |
|
94,52 |
0,26 |
0,67;11 |
2,28 |
6 |
1–56 |
|
136,55 |
0,43 |
0,92;15 |
2,69 |
9 |
1–60 |
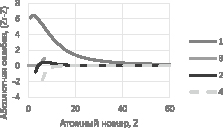
Рис. 3. Ошибка решения уравнения (4) для Е = 59,54 кэВ, где Zr:1 – Z0; 2 – по формуле (9); 3 – 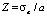 ; 4 – по формуле
; 4 – по формуле 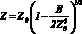
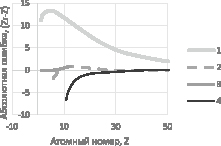
Рис. 4. Ошибка решения уравнения (4) для Е = 136,55 кэВ, где Zr: 1 – Z0; 2 – по формуле (9); 3 – 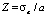 ; 4 – по формуле
; 4 – по формуле 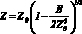
Для многоэлементных образцов
 , (10)
, (10)
а полный усредненный атомный коэффициент ослабления определяется по формулам (1–3)
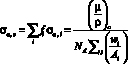 . (11)
. (11)
Тогда эффективный атомный номер сложной пробы для данной энергии E можно оценить следующим образом
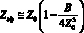 ,
, 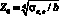 . (12)
. (12)
В Z0 (формула(12)) величина σа,с рассчитывается по формуле (11) с использованием табличных значений массового коэффициента ослабления или экспериментальных данных.
Формула (4) для многоэлементной пробы может быть записана в виде
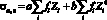 . (13)
. (13)
Тогда величины Z0 и Zэф приобретают следующий вид
 , (14)
, (14)
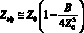 . (15)
. (15)
Учитывая, что величина B зависит от энергии излучения, то формулы (14, 15) описывают зависимость Zэф в явном виде, как от состава пробы, так и от энергии излучения. В = B(E) – единственный параметр, который зависит от энергии используемого излучения. Значения параметра B(E) в рассматриваемом диапазоне энергий приведены в табл. 1. Величины b(E), B(E) можно аппроксимировать зависимостями вида αEβ.
В табл. 3 приведены граничные значения Zε, при которых с точностью ε можно пренебречь фотоэлектрическим поглощением в (4) и вычислять атомный коэффициент ослабления по формуле 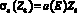 . Окончательно, для Zэф можно записать
. Окончательно, для Zэф можно записать
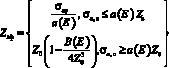 . (16)
. (16)
Значение Z0 (16) можно вычислять по формуле (12) или по формуле (14).
Таблица 3
Значения ε, Zε, и 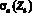 (барн/атом)
(барн/атом)
|
кэВ |
ε, % |
Zε |
σ(Zε) |
|
|
40,32 |
1 |
2,2 |
1,4 |
1,29 |
|
5 |
3,7 |
2,3 |
25 |
|
|
59,54 |
1 |
2,9 |
1,5 |
1,60 |
|
5 |
5,0 |
2,6 |
2,85 |
|
|
94,52 |
1 |
4,4 |
2,1 |
2,24 |
|
5 |
7,5 |
3,6 |
3,91 |
|
|
136,55 |
1 |
6,0 |
2,7 |
2,76 |
|
5 |
10,3 |
4,7 |
Примечание. * – получены линейной интерполяцией табличных значений XCOM для Z = Zε.
Результаты исследования и их обсуждение
В табл. 4, 5 сравниваются значения эффективных атомных номеров, рассчитанных по экспериментальным значениям полных атомных и массовых коэффициентов ослабления [3, 5] и теоретическим XCOM [4], используя полученные формулы (12) и (14, 15).
Таблица 4
Значения эффективных атомных номеров, полученных по экспериментальным данным работы [5] и рассчитанных по формулам (12, 14, 15) для энергии 59,54 кэВ (σа,с в единицах барн/атом)
|
Состав, wz, % |
|
|
|
|
|
|
Al-Fe(46,87) |
42,9 |
43,7 |
19,97 |
20,1 |
19,71 |
|
Al-Cu(07,55) |
17,93 |
17,8 |
15,04 |
15 |
14,94 |
|
Al-Zr(06,88) |
24,71 |
24,8 |
16,79 |
16,8 |
16,65 |
|
Al-Mo(09,87) |
33 |
31,1 |
18,42 |
14 |
18,27 |
|
Al-Pd(10,08) |
39,17 |
38,6 |
19,42 |
19,3 |
19,33 |
|
Al-Cd(09,64) |
40,73 |
38,8 |
19,66 |
19,4 |
19,6 |
|
Al-In(23,71) |
95,3 |
96,7 |
25,13 |
25,2 |
25,09 |
|
Al-Sn(07,84) |
37,42 |
36,6 |
19,15 |
19 |
19,15 |
|
Fe-Cu(08,48) |
118,34 |
127,1 |
26,67 |
27,2 |
26,28 |
|
Fe-Zr(07,72) |
136,66 |
136,4 |
27,73 |
27,7 |
27,34 |
|
Fe-Mo(11,04) |
153,16 |
156,6 |
28,6 |
28,8 |
28,22 |
|
Fe-Pd(11,27) |
167,75 |
170,7 |
29,3 |
29,4 |
28,97 |
|
Fe-Cd(10,79) |
172,1 |
172,7 |
29,51 |
29,5 |
29,21 |
|
Fe-In (26,05) |
276,89 |
291,1 |
33,46 |
33,9 |
33,26 |
|
Fe-Sn (08,80) |
166,41 |
171,1 |
29,24 |
29,5 |
28,97 |
Примечание. * – экспериментальная ошибка для  в интервале 3–8 %.
в интервале 3–8 %.
Таблица 5
Значения эффективных атомных номеров, полученных по экспериментальным** данным работы [3] и рассчитанным по формулам (12, 14, 15), для энергий в диапазоне 57–136 кэВ (σа,с в единицах барн/атом)
|
Состав |
Энергия, кэВ |
|
|
|
|
|
|
CuO |
57,5 |
96,47 |
125,5 |
26,5 |
24,65 |
24,2 |
|
77,1 |
46,25 |
50,9 |
24,9 |
24,2 |
24 |
|
|
94,6 |
29,07 |
31,7 |
24,5 |
23,77 |
23,8 |
|
|
136 |
15,2 |
15,2 |
23 |
23,01 |
23,28 |
|
|
Y2O3 |
57,5 |
234,53 |
241,3 |
31,6 |
31,35 |
30,81 |
|
77,1 |
107,15 |
128,9 |
32,6 |
30,94 |
30,6 |
|
|
94,6 |
63,69 |
65,2 |
30,7 |
30,52 |
30,35 |
|
|
136 |
27,72 |
30 |
30,2 |
29,36 |
29,59 |
|
|
BaCO3 |
57,5 |
437,9 |
470 |
37,6 |
36,9 |
37,23 |
|
77,1 |
202,56 |
198,6 |
36,6 |
36,82 |
36,99 |
|
|
94,6 |
119,31 |
127,8 |
37,3 |
36,59 |
36,68 |
|
|
136 |
47,85 |
42,6 |
34,1 |
343 |
35,62 |
Примечание. ** – ошибка экспериментальных данных оценивается в 8–10 % [5].
В формуле (12) использовалось полное атомное сечение, а в (14–15) сечение вычислялось по известным составам образцов. Экспериментальные массовые коэффициенты ослабления [3, 5] пересчитывались в атомные по формуле (11). В работе [3] экспериментально были получены массовые коэффициенты ослабления для прессованных образцов окислов CuO, Y2O3, а также BaCO3 высокой чистоты, их смесей и спеченных образцов, в диапазоне энергий 57–136 кэВ. В табл. 5 приведены полученные результаты для соединений.
Можно сделать вывод, что результаты, полученные по формулам (12), (14–15), хорошо согласуются между собой как с использованием экспериментальных, так и теоретических данных для разнообразных многоэлементных образцов в диапазоне энергий 57–136 кэВ. Сопоставление рассчитанных значений Zэф по предложенным формулам и прямой линейной интерполяцией по данным XCOM [4], используя полные атомные сечения, позволяет сделать вывод о хорошем их согласии.
Выводы
Полученная аналитическая зависимость для Zэф справедлива в широком диапазоне энергий, элементного состава вещества и обеспечивает согласие Zэф в пределах экспериментальных погрешностей при различных способах приготовления исследуемых образцов. Аналитическая зависимость эффективного атомного номера не только от состава вещества, но и от энергии позволит существенно упростить его вычисление и будет полезна в областях науки и техники, связанных с взаимодействием рентгеновского и гамма-излучения с веществом.




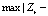 Z|; Z
Z|; Z *
*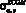

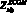 (12)
(12)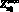 (12)
(12) (14, 15)
(14, 15)

 (12)
(12) (12)
(12) (14, 15)
(14, 15)