Задача выполнения прогноза фильтрационно-емкостных параметров нефтегазовых коллекторов и параметров флюидонасыщения (нефтегазоносности) по сейсмическим данным (атрибутам) на сегодняшний день является исключительно актуальной и научно значимой, поскольку ее решение составляет основу для подсчета запасов углеводородного сырья [1]. Объективно, при разведке месторождений нефти и газа, характеризующихся сложной построенностью изучаемой среды, недоопределенностью взаимосвязей между ее характеризующими параметрами и присутствующей «размытостью» исходных данных неизбежна неопределенность и многовариантность в результате моделирования прогнозных параметров продуктивности. Такая неопределенность дополнительно обусловлена неполнотой реально измеренных данных, наличием зон локальной неоднородности фильтрационно-емкостных характеристик продуктивного пласта.
Прогноз фильтрационно-емкостных параметров нефтегазовых коллекторов распадается на ряд подэтапов. Во-первых, это выработка тех параметров, которые по материалам на эталонной площади наилучшим образом обеспечивают качество прогноза фильтрационно-емкостных параметров, оцениваемое величиной ошибки прогноза. Эта процедура выполняется, например, с использованием факторного анализа [2]. Правильный подбор комбинаций сейсмических атрибутов в значительной степени определяет эффективность метода, и этому вопросу в настоящее время уделяется большое внимание [3–5]. Эти методы применяются и для близких задач, связанных с картированием зон трещиноватости [6]. Следующим подэтапом служит выработка обучающих правил прогноза и их настройка на эталонной площади [7, 8]. Собственно, этот этап предопределяет используемый метод прогнозирования.
После выбора атрибутов, и настройки прогнозирующей системы на особенности обучающей выборки сохраняется неопределенность исходных данных в значениях прогнозных параметров, которая выражается, например, в разбросе реальных значений параметра относительно получаемых в результате прогноза (на обучающей выборке). Это наиболее рельефно проявляется в случае использования регрессионных моделей. Разброс точек относительно линии регрессии служит неустраняемой компонентой и наследуется в результатах прогноза даже в том случае, когда не проявляется явно. Нет сомнения в том, что после выполнения прогноза в результатах будет наследоваться неопределенность, которую необходимо принимать во внимание. Дополнительной проблемой служит то, что в обучающей выборке параметры распределены неравномерно. Для одних областей значений параметров имеется густая сеть данных, а в других разброс и плотность данных меньше. Это сказывается на достоверности прогноза. Принятие для разных интервалов одного правила – регрессионной модели, приводит к появлению неконтролируемых ошибок, чреватых далеко идущими последствиями. Сами по себе эти погрешности – объективное проявление особенностей данных. Необходимо не прятать эту неопределенность в результатах за точечными цифрами, а давать реальную картину распределения достоверности прогноза в различных подобластях и для различных значений прогнозного параметра.
Возможность прогноза параметров с оценкой распределения достоверности, объективно отражающей особенности данных и связей между параметрами основана на том, что данные для обучения рассматриваются как отношения нечетких величин с последующим использованием в качестве прогнозного правила нечеткого логического вывода Мамдани [9, 10] по исходным данным, рассматриваемым как нечеткие переменные. Это позволяет получать результаты прогноза, согласованные с реальной неопределенностью и наследующие в себе различную степень достоверности данных различных интервалов обучающей модели. Основателем теории нечетких множеств является Лотфи Заде [11], а алгоритм нечеткого логического вывода был предложен Э. Мамдани [9]). Развернутое современное изложение теории нечеткого моделирования можно найти в работе [12].
Нечеткая величина σ полностью характеризуются своей функцией принадлежности 0 ≤ μ(σ) ≤ 1, имеющей смысл меры достоверности – возможности того, что измерение этой величины приведет к значению σ. Условием нормировки функции принадлежности служит: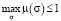 
, что в корне отличает функцию принадлежности от вероятностной меры. Этим обеспечивается и возможность организации эффективных вычислительных процедур на основе нечеткого логического вывода, и композиции нечетких отношений для моделирования итоговых функций принадлежности физико-геологических моделей.
Принципы использования аппарата нечеткой алгебры для прогнозирования в геолого-геофизических задачах можно найти в [13], а технология представления геолого-геофизических данных и экспериментально выявленных зависимостей в форме функций принадлежности и отношениями между нечеткими параметрами и правила логического вывода для прогноза параметров нечетких геотехнологических параметров разработаны в [14].
Рассмотрим применение данного метода на примере прогнозирования коэффициента нефтенасыщенности по интервальному времени прохождения продольной волны.
На временном разрезе, приведенном на (рис. 1), выделяем рассматриваемый пласт. В нем выделяем интервал для формирования прогнозного правила и интервалы пласта, для которых будет произведен прогноз коэффициента нефтенасыщенности по значениям интервального времени прохождения продольной волны.
Исходные данные для прогноза в форме полигонов измерений «пористость – интервальное время», «нефтенасыщенность – пористость» приведены на рис. 2.
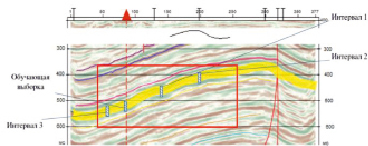
Рис. 1. Временной разрез
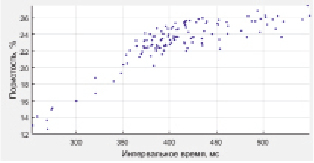
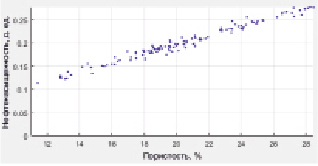
Рис. 2. Исходные данные зависимостей «пористость – интервальное время», «нефтенасыщенность – пористость»
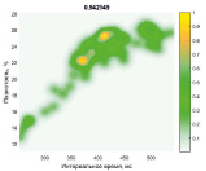
Рис. 3. Отношение нечетких величин «интервальное время – пористость»
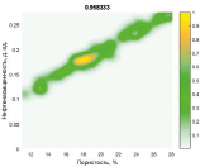
Рис. 4. Отношение между нечеткими величинами «пористость – нефтенасыщенность»
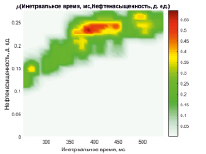
Рис. 5. Поле рассеяния композиции «интервальное время – нефтенасыщенность»
Выполним формирование нечетких отношений на основе данных «пористость – интервальное время», «нефтенасыщенность – пористость». Алгоритм такого формирования на основе расчета источников для функций принадлежности описан в работе [10].
Результат для исходных отношений приведен на рис. 3–4.
Выполняя композицию полученных отношений, получаем функцию принадлежности для отношения между нечёткими величинами «интервальное время» – «нефтенасыщенность», приведённую на рис. 5.
Приведённое отношение (рис. 5) служит искомым прогнозным правилом для формирования значения нечеткой переменной «нефтенасыщенность» по данным представленным в форме значения нечеткой переменной «интервальное время – нефтенасыщенность».
Далее выполняется прогноз значения нечеткой переменной нефтенасыщенность η(kн) по правилу нечеткого логического вывода в выбранных интервалах пласта Δli, основываясь на полученных результатах и данных сейсмического атрибута – нечеткой переменной «интервального времени прохождения продольной волны»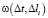 
.
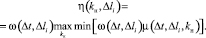
Здесь η(kн, Δli) – функция принадлежности для прогнозной нечеткой переменной «нефтенасыщенность», отнесенной к интервалу данных Δli.
Данные для расчета функции принадлежности интервального времени, отнесенного к заданным интервалам Δli глубин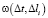 
, приведены ниже.
Оценка достоверности выполняется на основе аппарата α – сечений. Область Fαтех значений z, для которых μ(x) ≥ α ассоциируется с областью значений параметров, уровень доверия к которым не ниже величины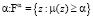 
. Традиционный уровень доверия и ширина области гарантированных значений, укладывающихся в эту оценку оцениваются по правилу {1 – α – α сечение}.
Можно заметить, что по мере изменения параметра α от нуля к единице эта область стягивается, вырождаясь в линию либо точку.
Выводы
Прогнозирование физико-геологических параметров по сейсмическим атрибутам может быть реализовано на основе технологии нечеткого моделирования, включающей в себя представление данных в форме нечетких отношений, конструирование итоговых отношений между нечеткими параметрами и выполнение прогноза по правилу нечеткого логического вывода.
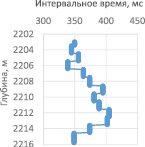
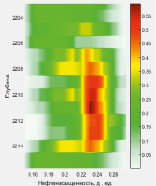
Рис. 6. Достоверность кривой нефтенасыщенности вдоль интервала № 1
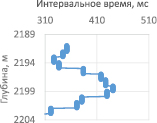
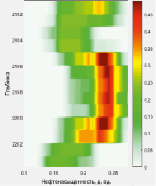
Рис. 7. Достоверность кривой нефтенасыщенности вдоль интервала № 2
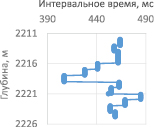
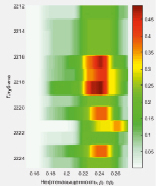
Рис. 8. Достоверность кривой нефтенасыщенности вдоль интервала № 3
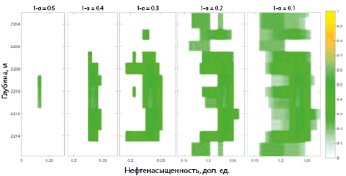
Рис. 9. Оценка достоверности полученных результатов на основе аппарата α – сечений для интервала № 1
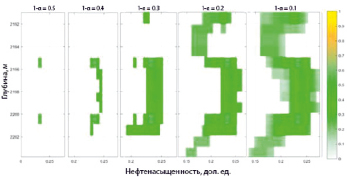
Рис. 10. Оценка достоверности полученных результатов на основе аппарата α – сечений для интервала № 2
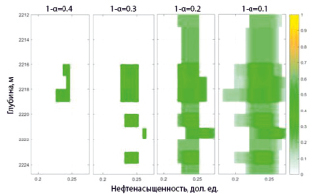
Рис. 11. Оценка достоверности полученных результатов на основе аппарата α – сечений для интервала № 3
Задача прогноза физико-геологических параметров на основе сейсмических атрибутов рассмотрена на примере прогнозирования нефтенасыщенности по интервальному времени прохождения сейсмических волн. Метод композиции нечетких отношений позволяет из цепочки отношений сконструировать требуемое, исключая промежуточные параметры. Оценка достоверности и связанная с ней ширина области неопределенности прогнозного параметра выполняется методом α сечений для функции принадлежности прогнозного параметра.