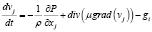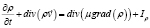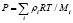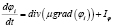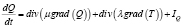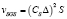Растущая антропогенная нагрузка отрицательно влияет на состояние приземного слоя атмосферы. В условиях современной действительности избежать поступления загрязняющих веществ (ЗВ) в воздушную экосистему невозможно. В настоящее время проводится широкий круг теоретических исследований по загрязнению атмосферного воздуха, основанных непосредственно на решении дифференциальных уравнений, задачи такого типа довольно сложные и с практической точки зрения очень значимы. В работах, посвященных данным проблемам, математическая постановка недостаточно универсальна.
Материалы и методы исследования
На перенос примесей в атмосфере оказывают значительное влияние ветровой режим и температурная стратификация приземного слоя атмосферы, а также метеорологические условия. Анализ и прогноз рассеивания ЗВ в атмосфере необходим для рационального размещения жилых районов и предприятий, производственные отходы которых влияют на здоровье и комфортные условия проживания. Задачи, посвященные анализу атмосферного воздуха, требуют большого объема исходных данных и сложных математических методов решения. В связи с ростом антропогенного воздействия на экосистемы актуальной задачей исследований является совершенствование математических моделей, предназначенных для оценки состояния воздушной среды. Эффективным путем решения указанной проблемы является математическое моделирование, позволяющее численно рассчитывать поля распространения ЗВ при различных ширине и плотности лесных массивов в приземном слое атмосферы. Использование комплекса взаимосвязанных математических моделей изменчивости газового и аэрозольного состава атмосферы дает возможность предсказать возможные перспективы развития экосистемы и последствия при разработке проектов застройки, озеленения и т.д.
Значимыми факторами развития воздушных экосистем являются аэродинамические процессы, определяющие перенос ЗВ и перемешивание воздушной среды.
Математическая модель процесса распространения примеси, представленная в работах [1, 2], дает теоретическое его описание, учитывает ряд физических факторов, влияющих на перенос примеси, и позволяет предсказать его ход и последствия.
В представленной модели рассеяние примеси учитывает турбулентность, распространение тепла и влажности, наличие лесных массивов, данные дополнительные условия образуют систему и начинают воздействовать как единая совокупность. Разрабатываемые модели также учитывают наличие лесных насаждений. Использование схем «кабаре» позволило авторам настоящей работы разработать математическую модель, обладающую свойством устойчивости для более широкого класса задаваемых входных параметров [3].
Комплекс моделей, использованных для описания движения воздушной среды, и распространение в ней примеси, представлен на рис. 1. Исходные уравнения модели отражены в таблице.
В таблице φi – объемные доли i-й фаз: воздуха, воды в газообразном состоянии, газа на источнике, воды в жидком состоянии, сажи, vj – проекции вектора скорости движения воздушной среды на оси Оxj, j = 1, 2, 3; λ – коэффициент теплопроводности, R – универсальная газовая постоянная, T – температура газовой фазы, Q – тепловая энергия, μ – коэффициент турбулентной диффузии, ρ – плотность, М – молярная масса, I – функция-источник, P – давление [4].
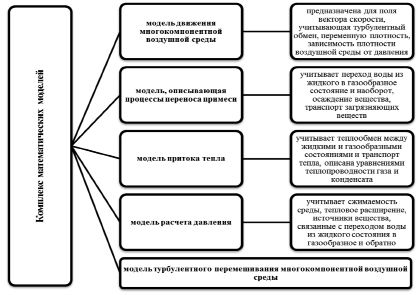
Рис. 1. Элементы комплекса взаимосвязанных моделей
Исходные уравнения модели
|
Уравнение движения (уравнение Навье – Стокса) |
|
|
Уравнение неразрывности (транспорта вещества) |
|
|
Уравнение состояния (аналог уравнения Менделеева – Клапейрона) |
|
|
Уравнение транспорта примеси |
|
|
Уравнение притока тепла |
|
|
Уравнение модели турбулентности |
|
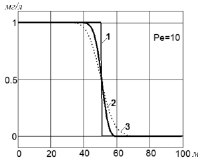
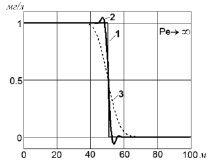
Рис. 2. Решения модельной задачи: 1 – точное решение задачи переноса; 2 – численное решение на основе предложенной разностной схемы при различных значениях чисел Пекле; 3 – численное решение задачи переноса на основе «против» потока
Для аппроксимации разработанной модели использован разностный метод [5–6]. Сопоставление результатов моделирования с натурными данными показало, что погрешность расчетов для предложенной модели составляет 10–15 % [1].
В случае если число Пекле меньше двух, наиболее эффективными являются центрально-разностные схемы. При решении прикладных задач применение данных схем влечет за собой увеличение размеров сеток и, как следствие, существенный рост трудоемкости. Также для решения подобного класса задач можно внедрять в схемы диссипативные слагаемые, что влечет за собой существенное падение точности решения и данный подход крайне нежелателен. В качестве примера схемы, обладающей диссипативными членами, можно назвать схему «левый уголок». Для преодоления данных проблем была разработана схема «кабаре», которая обладает свойством устойчивости и недиссипативности. Для оператора конвекции использована схема, полученная в результате линейной комбинации центральной разностной схемы и схемы «кабаре».
Рассмотрим нестационарное уравнение конвекции-диффузии [6, 7]
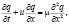(1)
где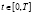 
, 
, 
, 
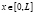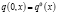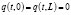, u = const.
Для аппроксимации оператора конвекции будем использовать схему, полученную в результате линейной комбинации центральной разностной схемы и схемы «кабаре»
;
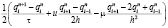
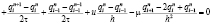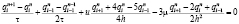. (2)
На рис. 2 представлены решения модельной задачи с начальными условиями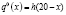 
, где h(x) – функция Хэвисайда (1 – точное решение задачи переноса, 2 – численное решение на основе разностной схемы (2), 3 – численное решение задачи переноса на основе схемы «левый уголок»).
Рассмотрим двумерное уравнение конвекции-диффузии
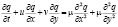, (3)
где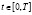 
, 
, 
, 
, 
, 
.
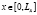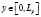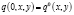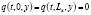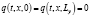Покроем область определения равномерной расчетной сеткой
,
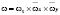где
, 
,
, 
.
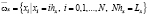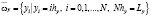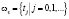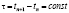Схема (2) для уравнения (3) будет иметь вид
;
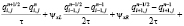
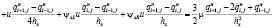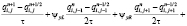
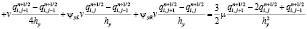, (4)
где ψxL = 1, ψxR = 0 при u > 0 и ψxL = 0, ψxR = 1 при u < 0; ψxL = 1, ψxR = 0 при v > 0 и ψxL = 0, ψxR = 1 при v < 0.
Результаты исследования и их обсуждение
Разработанные модель, алгоритмы, ее реализующие, построенный комплекс программ позволили выполнить численные эксперименты по моделированию распространения ЗВ в приземном слое атмосферы при наличии лесных массивов. Изучено влияние наличия растительности на распределение ЗВ под действием восходящих потоков воздуха. Исходные данные: плотность воздушной среды 1,29 кг/м3; плотность выброса 1,4 кг/м3; температура окружающей среды 20 °С; температура выброса 120 °С; скорость течения воздушной среды 1 м/с в направлении прибрежной зоны; удельная мощность выброса 5 л/с; скорость движения воздушной среды на левой границе 1 м/с; коэффициент проницаемости воздушной средой растительного покрова 50 %; высота растительного покрова 30 м, ширина области растительного покрова 50 м [5]. Палитрой показана концентрация примеси. Выполнены численные эксперименты по моделированию движения загрязняющих веществ при наличии лесных насаждений (рис. 2) и при их отсутствии (рис. 3). Область лесных насаждений обозначена прямоугольником.
Рис. 3. Поле концентраций примеси с учетом растительности
Рис. 4. Поле концентраций примеси
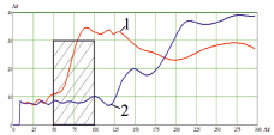
Рис. 5. Траектории распространения загрязняющих веществ
Градация цвета иллюстрирует концентрацию примеси. Анализ рис. 3 и 4 позволяет сделать вывод, что наличие лесных насаждений влияет на распределение загрязняющих веществ. Примеси под действием восходящих потоков воздуха поднимаются вверх в области лесных насаждений. На рис. 5 представлено движение воздушной среды в случае наличия лесных насаждений. Градацией цвета показана интенсивность движения воздушной среды.
Рисунок иллюстрирует поле скорости движения воздушной среды в случае наличия лесных насаждений и вихревые структуры течения воздушной среды, расположенные за областью лесных насаждений по направлению движения ветра. Скорость движения воздушной среды усиливается в отдельных областях в три раза.
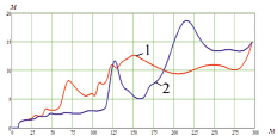
Рис. 6. Ширина трубок тока
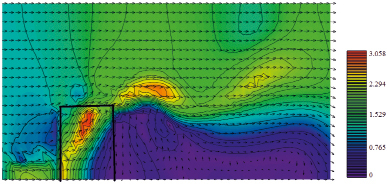
Рис. 7. Движения воздушной среды в случае наличия лесных насаждений
Рис. 5 демонстрирует уменьшение ширины трубки тока в области лесных насаждений. На рис. 6 представлено поле скорости движения воздушной среды в случае наличия лесных насаждений. Палитрой показана интенсивность движения воздушной среды.
Наличие лесных насаждений влияет на распределение загрязняющих веществ. Примеси под действием восходящих потоков воздуха поднимаются вверх в области лесных насаждений. На рис. 5 показаны траектории распространения загрязняющих веществ: 1 – наличие полупроницаемой области, 2 – отсутствие полупроницаемой области. На рис. 6 приведены зависимости ширины трубок тока, по которым распространяются загрязняющие вещества в случае наличия полупроницаемой области и ее отсутствия.
Рис. 7 иллюстрирует вихревые структуры течения воздушной среды, расположенные за областью лесных насаждений по направлению движения ветра. Скорость движения воздушной среды усиливается в отдельных областях в три раза. Далее исследовалось влияние ширины области лесных насаждений на поля скорости движения воздушной среды и концентрации примеси.
Выводы
Предложенные методы математического моделирования движения воздушных потоков позволяют оценить влияние лесных насаждений на распространение ЗВ в приземном слое атмосферы и изменение коэффициента турбулентного обмена. Разработанная модель учитывает переход воды из жидкого в газообразное состояние, осаждение вещества, транспорт примеси и тепла, теплообмен между жидкими и газообразными состояниями.
Научная новизна представленных результатов состоит в том, что для аппроксимации оператора конвекции использована схема, полученная в результате линейной комбинации центральной разностной схемы и схемы «кабаре». Использование схем «кабаре» позволяет повысить условия применимости разработанной модели. Построенные алгоритмы реализованы в виде программного комплекса, позволяющего определять влияние наличия растительности на распределение ЗВ под действием восходящих потоков воздуха. Разработанные модель, алгоритмы, ее реализующие, построенный комплекс программ позволили выполнить численные эксперименты по моделированию распространения ЗВ в приземном слое атмосферы при наличии лесных массивов. Преимущество модели движения воздушной среды – возможность учета влияния лесных массивов и турбулентного перемешивания в уравнении неразрывности среды.
Работа выполнена при поддержке РНФ (проект № 17–11–01286).