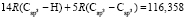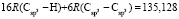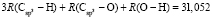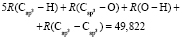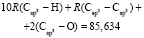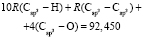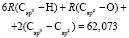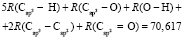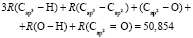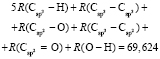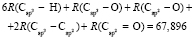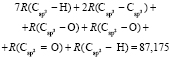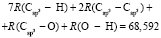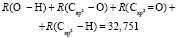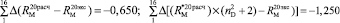В настоящее время рефрактометрия используется как предварительное исследование к спектроскопическим методам определения структуры молекул [1–3]. При этом предполагается, что молекулярная рефракция может быть представлена в виде суммы молекулярных рефракций химических связей RMi (X – Y), образующих молекулу. Вклады в молекулярную рефракцию вещества определяются из формулы (1) и табулированы [4, 5]
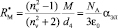 , (1)
, (1)
где 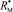 – молекулярная рефракция исследуемого вещества, nn – абсолютный показатель преломления на частоте n, aэл – среднее значение электронной поляризуемости молекулы, d4 – плотность вещества, NA = 6,022×1023 моль-1, М – молярная масса, e0 = 8,85419×10-12 Ф/м.
– молекулярная рефракция исследуемого вещества, nn – абсолютный показатель преломления на частоте n, aэл – среднее значение электронной поляризуемости молекулы, d4 – плотность вещества, NA = 6,022×1023 моль-1, М – молярная масса, e0 = 8,85419×10-12 Ф/м.
Цель исследования
В работе поставлена задача модернизировать метод аддитивности молекулярной рефракции вещества. В [6] показано, что молекулярная рефракция RM должна определяться из выражения
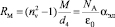 . (2)
. (2)
Из левых частей формул (1) и (2) следует, что величина отношения 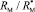 равна
равна 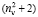 . Очевидно, что суммарное значение молекулярных рефракций химических связей анализируемых молекул также будет отличаться в
. Очевидно, что суммарное значение молекулярных рефракций химических связей анализируемых молекул также будет отличаться в 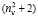 раза. В случае разреженного газа величина (
раза. В случае разреженного газа величина (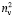 + 2) примерно равна 3, поэтому значения
+ 2) примерно равна 3, поэтому значения 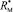 незначительно отличаются от значений RM, что позволяет использовать выражение (1) для оценки величины aэл и в настоящее время. В плотных средах величина отношения (
незначительно отличаются от значений RM, что позволяет использовать выражение (1) для оценки величины aэл и в настоящее время. В плотных средах величина отношения (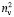 + 2)/3 заметно больше 1. Например, у воды на линии насыщения при 20 °С величина
+ 2)/3 заметно больше 1. Например, у воды на линии насыщения при 20 °С величина 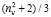 в жидкой фазе равна 1,25926, а в газовой фазе – 1,000004 [7]. Естественно, что в плотных средах формула Лоренца – Лоренца непригодна для расчета значений aэл. Модифицированные формулы Лоренца – Лоренца [7] уменьшают погрешность расчета показателей преломления вещества, но не дают точных определений величины электронной поляризуемости молекул.
в жидкой фазе равна 1,25926, а в газовой фазе – 1,000004 [7]. Естественно, что в плотных средах формула Лоренца – Лоренца непригодна для расчета значений aэл. Модифицированные формулы Лоренца – Лоренца [7] уменьшают погрешность расчета показателей преломления вещества, но не дают точных определений величины электронной поляризуемости молекул.
Материалы и методы исследования
В настоящей работе для расчета значений RM вещества и химических связей используется формула (2). Значения RM рассчитываются по справочным данным работ [4, 8]. Расчет значений RM различных по природе веществ ведется для 20 °С и для желтой линии натрия (589,26 нм). Учет температуры необходим для стандартизации энергетического состояния молекул.
Для классификации химических связей используется понятие гибридизации атомов углерода. Гибридизация атомов углерода позволяет частично учесть ближнее окружение атомов данной связи и избавиться от «экзальтаций», использующихся в рефрактометрическом методе. Естественно, что строгой аддитивностью данный метод не обладает, так как он не учитывает все «ближнее» окружение данной связи, и поэтому он применяется для получения предварительной информации о структуре молекулы.
Из формулы (2) следует, что абсолютный показатель преломления определяется величиной электронной поляризуемости молекул [9, 10]. Следовательно, формула (2) наиболее непосредственным образом связывает макроскопические свойства вещества (показатель преломления и плотность) с поляризуемостью молекулы.
Результаты исследования и их обсуждение
Для расчета значений 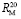 химических связей представим молекулярную рефракцию воды в виде суммы молекулярных рефракций связей (О–Н):
химических связей представим молекулярную рефракцию воды в виде суммы молекулярных рефракций связей (О–Н):
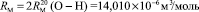 .
.
Обозначая 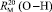 как х0, получаем
как х0, получаем 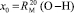 = 7,005×10-6м3/моль. Используя значения nn и d4 молекул тетрахлорметана (CCl4: nn = 1,46018, d4 = 1594,03 кг/м3, М = 153,823×10-3 кг/моль [8]) и дихлорметана (CН2Cl2: nn = 1,42416, d4 = 1325,60 кг/м3, М = 84,930×10-3 кг/моль [8]), находим: х1 = 5,627×10-6 м3/моль. Из данных по nn и d4 гексана и х1 = 5,627×10-6 м3/моль определяем величину рефракции связи
= 7,005×10-6м3/моль. Используя значения nn и d4 молекул тетрахлорметана (CCl4: nn = 1,46018, d4 = 1594,03 кг/м3, М = 153,823×10-3 кг/моль [8]) и дихлорметана (CН2Cl2: nn = 1,42416, d4 = 1325,60 кг/м3, М = 84,930×10-3 кг/моль [8]), находим: х1 = 5,627×10-6 м3/моль. Из данных по nn и d4 гексана и х1 = 5,627×10-6 м3/моль определяем величину рефракции связи 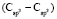 :
: 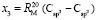 = 7,516×10-6 м3/моль. Из данных по nn и d4 этанола (RM = 49,822×10-6 м3/моль) и ранее найденных значений х0, х1 и х3 определяем величину
= 7,516×10-6 м3/моль. Из данных по nn и d4 этанола (RM = 49,822×10-6 м3/моль) и ранее найденных значений х0, х1 и х3 определяем величину 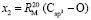 = 7,166×10-6 м3/моль.
= 7,166×10-6 м3/моль.
Далее, обозначая молекулярные рефракции химических связей, входящих в уравнения для RM ацетона (62,201), ацетальдегида (43,703), метилацетата (67,673), ацетилхлорида (65,926), тетрахлорметана (129,504), гексена-1 (115,797), муравьиной кислоты (33,230), диметилкарбоната (73,592) и 2-метил-1-бутена (96,877×10-6 м3/моль), как х4, х5, х6, х7, х16 и х26 соответственно, составляем систему линейных уравнений. Для полученной переопределенной системы уравнений методом наименьших квадратов находим решение минимальной нормы при х0 = 7,005; х1 = 5,627; х2 = 7,166 и х3 = 7,516×10-6 м3/моль, а полученные значения заносим в табл. 1:
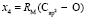 = 8,021;
= 8,021;
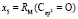 = 9,583;
= 9,583;
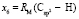 = 8,142;
= 8,142; 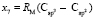 = 9,364;
= 9,364;
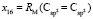 = 9,122;
= 9,122; 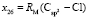 = 27,312×10-6 м3/моль.
= 27,312×10-6 м3/моль.
Расчеты были сделаны в программном пакете MATLAB.
Из молекулярной рефракции этилаллена (С5Н8: М = 68,120×10-3 кг/моль, nD = 1,42091, d4 = 692,57 кг/м3 [4])
RM = 3х6 + 2х37 + х7 + 5х1 + х3 = 100,226×10-6 м3/моль
по известным х1, х3, х6 и х7 находим величину 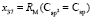 = 15,392×10-6 м3/моль. Для нахождения значений
= 15,392×10-6 м3/моль. Для нахождения значений 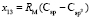 ,
, 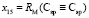 ,
, 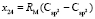 ,
, 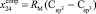 ,
, 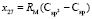 ,
, 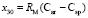 и
и 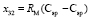 требуется определить молекулярные рефракции связей
требуется определить молекулярные рефракции связей 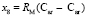 ,
, 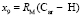 и
и 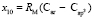 . Величину молекулярной рефракции х10 (4,128×10-6 м3/моль) определяем из уравнения для n-ксилола, а х8 и х9 находим из системы уравнений для бензола (С6Н6), пиридина (С6Н5 N) и хинолина (С9Н7 N):
. Величину молекулярной рефракции х10 (4,128×10-6 м3/моль) определяем из уравнения для n-ксилола, а х8 и х9 находим из системы уравнений для бензола (С6Н6), пиридина (С6Н5 N) и хинолина (С9Н7 N):
(6x8 + 6x) = 111,381×10-6 м3/моль) – бензол,
(4x8 + 5x9 + 2x17 = 103,027×10-6 м3/моль) – пиридин,
(9x8 + 7x9 + 2x17 = 194,636×10-6 м3/моль) – хинолин.
Отсюда имеем
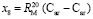 = 18,160×10-6 м/моль,
= 18,160×10-6 м/моль,
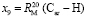 = 0,404×10-6 м/моль,
= 0,404×10-6 м/моль,
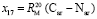 = 14,184×10-6 м/моль.
= 14,184×10-6 м/моль.
Из молекулярных рефракций RM акрилонитрила С3Н3N (61,563), фенилацетилена С8Н6 (153,013), пропаргилового эфира уксусной кислоты С5Н6О2 (99,324), тетрилового альдегида С4Н4О (80,261), бензилцианида C8H7N (152,002), нитрил амилпропиоловой кислоты С8Н11N (159,189), бензонитрила С6Н5N (136,958), циановодорода НСN (23,288) и 5-децина С10Н18 (190,911×10-6 м3/моль) составляем систему линейных уравнений. Решаем ее методом наименьших квадратов, используя ранее найденные значения х0 – х9 и х16. Полученные значения (х13, х15, х24, 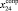 , х27 – х30 и х32) заносим в табл. 1.
, х27 – х30 и х32) заносим в табл. 1.
Таблица 1
Значения молекулярных рефракций углерод-углеродных связей (С – С) при 20 °С
|
Связь |
xi |
|
|
|
Настоящая работа |
Рефракции по Фогелю [4] |
||
|
1 |
2 |
3 |
4 |
|
|
x3 |
7,516 |
|
|
|
x7 |
9,364 |
То же |
|
|
x13 |
7,148 |
То же |
|
|
x10 |
4,128 |
То же |
|
|
x24 |
12,309 |
То же |
|
|
|
20,308 |
То же |
|
Окончание табл. 1 |
|||
|
1 |
2 |
3 |
4 |
|
|
x16 |
9,122 |
4,17 |
|
|
x27 |
10,315 |
|
|
|
х14 |
11,414 |
То же |
|
|
x37 |
15,392 |
– |
|
|
x15 |
27,371 |
6,24 (не концевая) |
|
|
x8 |
18,160 |
2,688; 2,69 |
|
|
x30 |
9,986 |
|
|
|
x32 |
15,069 |
|
В табл. 2 приведены значения молекулярных рефракций химических связей атома углерода с другими атомами (X).
Таблица 2
Значения связей 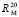 (С – X) при 20 °С [4]
(С – X) при 20 °С [4]
|
Связь |
|
Связь |
|
|
(С – Н) |
1,676 |
(N – H) |
1,76 |
|
(С – Сl) |
6,51 |
(N – O) |
2,43 |
|
(С – O), эфиры |
1,54 |
(O – H), спирты |
1,66 |
|
(С – O), ацетали |
1,46 |
(O – H), кислоты |
1,80 |
|
(С = О) |
3,32 |
(С – С), циклопропан |
1,50 |
|
(С = O), метилкетон |
3,49 |
(С – С), циклобутан |
1,38 |
|
(С – N |
1,57 |
(С – С), циклопентан |
1,27 |
|
(С = N) |
3,75 |
(С – F) |
1,55 |
|
(С - N) |
4,82 |
(С – Br) |
9,39 |
Примечание. Величина 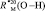 в воде из формулы (2) равна 1,854×10-6м3/моль.
в воде из формулы (2) равна 1,854×10-6м3/моль.
Для сравнения величин молярных рефракций, найденных по данным табл. 1 (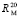 ) и табл. 1; 2 (
) и табл. 1; 2 (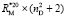 ), рассчитаем значения молекулярных рефракций исследуемых веществ и занесем их в табл. 3.
), рассчитаем значения молекулярных рефракций исследуемых веществ и занесем их в табл. 3.
Таблица 3
Значения молекулярных рефракций некоторых веществ
|
Вещество |
Молекулярная рефракция, 10-6 м3/моль |
|
[4, 8] |
|
|
|
|
|||
|
1 |
2 |
3 |
4 |
5 |
|
ССl4, тетрахлорметан |
|
107,601 |
4,132126 |
109,249 |
|
СH2Сl2, дихлорметан |
|
65,950 |
4,028232 |
65,878 |
|
C6H14, гексан |
|
116,489 |
3,890240 |
116,358 |
|
Окончание табл. 3 |
||||
|
1 |
2 |
3 |
4 |
5 |
|
C7H16, гептан |
|
135,792 |
3,925544 |
135,638 |
|
CH3OH, метанол |
|
30,976 |
3,764646 |
30,971 |
|
C2H5OH, этанол |
|
49,618 |
3,853492 |
49,822 |
|
C4H10О, этоксиэтан |
|
85,904 |
3,829527 |
86,162 |
|
C4H10О2, 1,2-диметоксиэтан |
|
92,433 |
3,868142 |
92,029 |
|
C3H6О, пропанон |
|
62,067 |
3,846039 |
62,201 |
|
C3H5О2, 2-оксопропанол (ацетилкарбинол) |
|
71,092 |
4,043470 |
71,416 |
|
С2Н4О2, этановая кислота |
|
50,755 |
3,882110 |
50,472 |
|
C3H6О2, пропановая кислота |
|
6 9,557 |
3,924879 |
69,070 |
|
C3H6О2, метилацетат |
|
67,789 |
3,853410 |
67,673 |
|
C4H8О2, пропилформиат |
|
87,308 |
3,895936 |
87,175 |
|
C3H8О, пропанол-1 |
|
68,925 |
3,919776 |
68,783 |
|
CH2О2, метановая кислота |
|
32,698 |
3,880656 |
33,226 |
|
|
||||
«Экспериментальные» значения молекулярных рефракций находились из формулы (2) по справочным данным абсолютного показателя преломления и плотности [4, 8]. Из табл. 3 видно, что величина среднего отклонения молекулярной рефракции из 16 различных по природе веществ 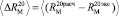 по нашим данным практически равна величине
по нашим данным практически равна величине 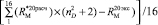 . При этом следует отметить, что значения молекулярных рефракций некоторых связей (О–H),
. При этом следует отметить, что значения молекулярных рефракций некоторых связей (О–H), 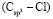 ,
, 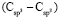 и
и 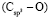 имеют однозначные величины. Этот факт, кроме знаменателя {
имеют однозначные величины. Этот факт, кроме знаменателя {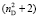 } в формуле (1), является одной из причин расхождения значений молекулярных рефракций химических связей, определенных нами и в литературе [4].
} в формуле (1), является одной из причин расхождения значений молекулярных рефракций химических связей, определенных нами и в литературе [4].
Заключение
Таким образом, в настоящей работе предложен метод расчета значений молекулярной рефракции химических связей, основанный на теоретически обоснованном выражении для RM, что позволяет рассчитывать значения электронной поляризуемости различных по природе молекул в реальном веществе, в то время как формула Лорентц – Лоренца в настоящее время используется как первое приближение только для сильно разреженных газов.




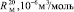
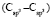
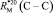 = 1,296
= 1,296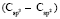
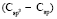
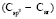
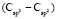
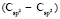
 (сопряженные диены)
(сопряженные диены)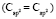
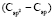
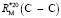 = 1,296
= 1,296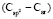
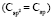
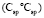
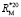 (C - C): 5,87 (концевая),
(C - C): 5,87 (концевая),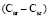
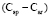
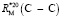 = 1,296
= 1,296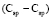
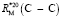 = 1,296
= 1,296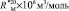
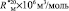
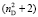
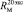
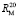
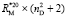
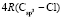 = 109,248
= 109,248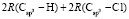 = 65,878
= 65,878