В последнее время, в связи с автоматизацией управления лесным хозяйством, большое значение приобретают модели роста древостоев. При этом последние, как правило, используются при проведении таксации лесов способом актуализации, указанном в лесоустроительной инструкции [1], заключающемся в уточнении таксационных описаний предыдущего лесоустройства. Однако, несмотря на типовой подход, в настоящее время наблюдается дефицит корректной информации о лесном фонде для лесных участков в целом. Обычно это связано с низким качеством исходных данных, в том числе из-за человеческого фактора, обусловленного проведением выборочной натурной таксации и актуализации отдельных лесных выделов, отобранных методом экспертной оценки [2, 3]. Решение данной проблемы представляется ряду специалистов проведением компьютерной идентификации древостоев и их состояний на всей территории по космическим снимкам высокого разрешения (например, методом распознавания образов). Однако подобная идентификация нуждается в проверке адекватности ввиду удаленности изучаемых объектов. Проводимая в данном направлении работа, несмотря на возможность получения характеристики лесных массивов в целом, до сих пор не привела к решению проблемы [4].
В связи с вышеизложенным, отметим, что появилось смещение акцентов в сторону применения альтернативных методов таксации, в том числе анализа данных дистанционного зондирования. Подобная тенденция не позволяет полностью отказаться от выборочно-статистического метода инвентаризации, так как разработка моделей роста древостоя для актуализации лесоустроительной информации лесных участков полностью может использоваться как для самостоятельной оценки, так и для проверки адекватности альтернативных методов [5].
Целью исследования являлась разработка моделей роста древостоев для характерных участков на примере Чайковского лесничества с целью актуализации лесоустроительной информации.
Материалы и методы исследования
Чайковское лесничество расположено в зоне хвойно-широколиственных лесов в юго-западной части Пермского края на территории двух муниципальных районов: Еловского и Чайковского. Протяженность территории лесничества с севера на юг составляет около 70 км, с востока на запад – 116 км. Общая площадь лесничества Чайковское – 22706 га, в том числе 13517 га – защитные, 9189 га – эксплуатационные [6]. Климат умеренно континентальный. Период вегетации имеет продолжительность около 130 дней. За год выпадает около 550 мм осадков.
В соответствии с методикой [7] по таксационным показателям строилась регрессионная модель, которая позволяет учесть естественный рост древостоев и может быть применима для прогнозирования. В работе использована электронная база лесотаксационных данных Чайковского лесничества Пермского края. Применимость данного метода связана с широким использованием материалов лесоустройства, в том числе в соответствии с Н.П. Анучиным [8], возможностью устанавливать закономерности хода роста древостоев.
Анализ исходных материалов показал, что в районе исследований наиболее представленными являются еловые древостои, произрастающие на дренированных участках с устойчивым водным режимом. Поэтому основное внимание было уделено изучению динамики таксационных показателей данных древостоев. Однако, учитывая, что в пределах выбранных участков производительность ельников существенно различается (с I по III класс бонитета), в работе более тщательное внимание уделялось разработке моделей, характеризующих ход роста для модальных лесорастительных условий соответствующих II классу бонитета, аккумулирующего наибольший объем экспериментального материала. Далее в пределах данного класса бонитета таксационные выделы были распределены по относительным полнотам, для учета специфики роста, связанной с первоначальной густотой и ходом последующего изреживания насаждений.
С использованием регрессионного анализа методом наименьших квадратов отклонений по выборке строились модели роста для трех основных таксационных показателей древостоев: средней высоты, среднего диаметра и запаса древесины на одном гектаре. В качестве критерия адекватности полученной регрессионной модели рассматривался коэффициент детерминации (R2 > 0,9). Принималось предположение, что рассматриваемая выборка имеет нормальное распределение. Поэтому в качестве критерия достоверности регрессионных коэффициентов в модели рассматривались коэффициенты Стьюдента.
На основе полученных моделей возрастной динамики таксационных показателей и отмеченных особенностей изменения текущего прироста составлены справочные материалы в виде таблиц годичных приростов таксационных показателей по n-летним ступеням возраста для актуализации лесотаксационных материалов. С их использованием проведен перерасчет устаревших данных. Согласно лесоустроительной инструкции [1] проверка актуализированных показателей произведена путем сопоставления полученных материалов с данными натурной таксации. Для проверки методом случайной выборки отобраны 30 выделов, пройденных натурной таксацией.
В качестве базовых уравнений приняты наиболее подходящие для описания изменений основных таксационных показателей древостоев, которые позволяют произвести учет зависимостей средней высоты и среднего диаметра древостоев от их возраста, согласно рекомендациям Н.П. Анучина [8], уравнение Корсуня:
Y = X2/(c + b×X + a×X2), (1)
где Y – значение таксационного показателя (диаметра в см и высоты в м);
Х – средний возраст древостоя, лет;
а, b, c – регрессионные коэффициенты уравнения.
И оценка запасов с помощью уравнения Корсуня – Бакмана [4]:
lnY = c + b×ln Х + а×ln2Х, (2)
где Y – запас древостоя, м3;
Х – возраст древостоя, лет;
а, b, c – регрессионные коэффициенты уравнения.
Использование данных уравнений позволяет сопоставлять полученные закономерности прироста с данными других исследований [5].
Результаты исследования и их обсуждение
С использованием уравнения (1) по исходным данным получены статистически достоверные коэффициенты для уравнения регрессии по полученному объему выборки (N) зависимости высоты (H, м) от возраста древостоя (A, лет), значения которых приведены в табл. 1.
Таблица 1
Значения коэффициентов уравнения Н = А2 / (a×А2 + b×А + c) для еловых насаждений II класса бонитета
|
Класс бонитета |
Значения коэффициентов (числитель) и критерия Стьюдента (знаменатель) |
R2 |
||
|
a |
b |
c |
||
|
II |
0,0232 / 12,4 |
1,3556 / 7,3 |
26,9322 / 5,7 |
0,97 |
На рис. 1 приведен график хода роста, полученный на основе регрессионной модели возрастной динамики еловых древостоев второго класса бонитета, без учета влияния относительной полноты насаждения, в сопоставлении с исходными данными лесоустройства.
С использованием уравнения Корсуня получена возрастная динамика диаметров деревьев (D, см) по исследуемому участку. Параметры модели приведены в табл. 2.
Таблица 2
Значения коэффициентов регрессии и их характеристики по уравнению D = А2 / (a×А2 + b×А + c) по II классу бонитета и относительной полноте 0,6
|
Класс бонитета |
Значения коэффициентов (числитель) и критерия Стьюдента (знаменатель) |
R2 |
||
|
a |
b |
c |
||
|
II |
0,0183 / 5,05 |
0,8776 / 2,27 |
33,9495/ 3,21 |
0,92 |
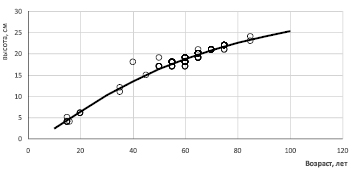
Рис. 1. Возрастная динамика средней высоты еловых насаждений II класса бонитета. Линией обозначена модель, кружочками – исходные данные
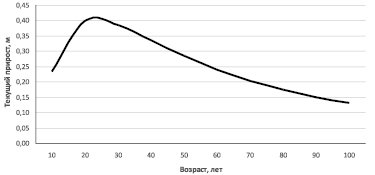
Рис. 2. Возрастная динамика текущего прироста древостоев по высоте в еловых древостоях II класса бонитета
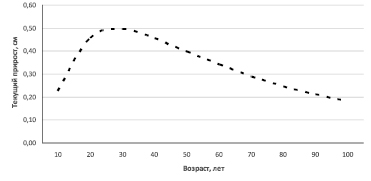
Рис. 3. Возрастная динамика текущего прироста по диаметру ельников II класса бонитета с относительной полнотой 0,6
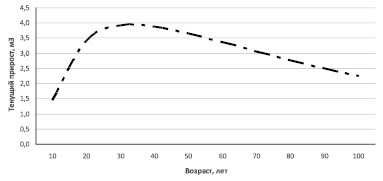
Рис. 4. Возрастная динамика текущего прироста по запасу насаждений II класса бонитета с относительной полнотой 0,6
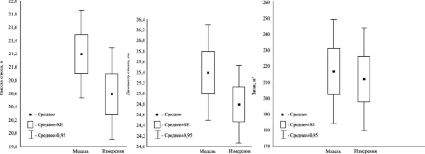
Рис. 5. Сравнение результатов актуализации по модели и натурного обследования: среднее – среднее арифметическое; SE – стандартная ошибка; 0,95 – 95 % – доверительный интервал
В результате анализа было выявлено существенное влияние относительной полноты на рост ельников по диаметру, в связи с чем модель разработана для модальных еловых древостоев второго класса бонитета с относительной полнотой 0,6.
Для выравнивания запасов использовалась функция Корсуня – Бакмана (2). В результате получена статистически достоверная регрессионная модель.
Далее, учитывая, что наиболее эффективным приемом актуализации является использование в этом процессе экстраполяционных коэффициентов, представляющих собой величины изменения таксационных показателей за определенное количество лет, был проведен анализ приростов по высоте (рис. 2).
Возрастная динамика текущего прироста по диаметру в молодом возрасте описывается аналогичным образом, достигая кульминации в 30 лет (рис. 3).
Возрастная динамика текущего прироста по запасу характеризуется кульминацией в 30 лет (рис. 4), после чего с возрастом прирост также постепенно снижается.
Проведенный анализ по приростам позволил разработать экстраполяционные коэффициенты, представляющие собой величины изменения таксационных показателей за определенное количество лет (приросты по высоте, диаметру и запасу в %). Полученные данные, сгруппированные в зависимости от возраста насаждения, позволили произвести пересчет данных прошлого лесоустройства с учетом срока их давности.
Сопоставление результатов натурного обследования с модельными данными показало, что в среднем наибольшее расхождение по запасу не превышает 10 %. В результате оценки по модели получены значения, превышающие результаты натурного обследования (рис. 5). Однако статистически значимого различия средних между модельными расчетами и результатами натурного обследования установить не удалось.
В результате проведенной работы:
– Получены коэффициенты регрессии, позволившие определить среднегодовое изменение средних высоты, диаметра и запаса на 1 га в различном возрасте древостоев. Составлена таблица текущего прироста еловых древостоев по основным таксационным показателям.
– Для проверки адекватности разработанных моделей, на основе полученной таблицы текущего прироста, таксационной характеристики выделов и периода с момента проведения предыдущего лесоустройства проведена актуализация средних диаметров, средних высот и запасов на 1 гектар. Сравнение значений таксационных показателей в выделах, пройденных натурной таксацией, с данными, полученными в результате актуализации, показало адекватность полученных моделей.
– Получены модели, характеризующие рост древостоев с учетом особенностей условий произрастания, применимые при составлении местных таблиц хода роста еловых древостоев, которые могут быть использованы как для характеристики рассмотренного лесного фонда, так и для проверки адекватности актуализации материалов, выполненной другими способами.
Выводы
Использование уравнения Корсуня для описания возрастной динамики средней высоты и среднего диаметра еловых древостоев, а также уравнения Корсуня – Бакмана для описания запасов позволяет получить достоверные регрессионные коэффициенты.
Материалы лесоустройства надлежащего качества в сочетании с результатами измерительно-перечислительной таксации позволяют получать объективные данные о возрастной динамике основных таксационных показателей древостоев и могут служить основой для проведения лесоустройства методом актуализации.



