Высокая степень антропогенного воздействия на биосферу в последние десятилетия привела к фундаментальным изменениям в структуре и конфигурации ландшафтов. Многие ученые отмечают, что разрушение и фрагментация ландшафтов являются важнейшими факторами глобального снижения биоразнообразия [1]. Фрагментация ландшафтов приводит к неоднородности распределения жизненно важных ресурсов, к нарушению энергетического обмена, к серьезным изменениям климатического режима и ряда других факторов. Таким образом, физические преобразования пространственной структуры ландшафтов влияют на поведение организмов, внутри- и межвидовые взаимодействия, структуру и динамику популяций [1]. При этом результаты эмпирических исследований указывают на то, что фрагментация и изоляция мест обитания негативно сказывается на устойчивости как животных, так и растительных сообществ. Несмотря на то, что наиболее фрагментированные ландшафты находятся именно в городах, экологическое значение связанности мест обитания в урбанизированной среде изучено недостаточно [2]. В некоторой степени это связано с отсутствием универсальных методик для оценки степени связанности и дискретности ландшафтов.
Таким образом, цель данной работы заключается в разработке методики для комплексной оценки связанности биотопов в городских ландшафтах.
Материалы и методы исследования
В научной литературе встречается несколько подходов к феномену фрагментации ландшафтов. Различаются они тем, как биотоп рассматривается относительно других элементов ландшафта. Несмотря на то, что существует множество вариаций, можно выделить всего две основные парадигмы, определяющие структуру ландшафта и порядок взаимодействия его компонентов. Первая парадигма – динамическая модель ландшафтной мозаики, где ландшафт воспринимается как сложная система, которую невозможно упростить до дихотомии среды обитания и матрицы [1]. В рамках второй парадигмы, «статической модели островной биогеографии», дискретные фрагменты естественного ландшафта рассматриваются как особые включения в единой матрице, непригодной для обитания [1].
В условиях городской застройки биотопы находятся в относительно статичной матрице. Поэтому для оценки степени связанности мест обитания в городской среде многие ученые используют статическую модель: она позволяет достаточно просто представить структуру ландшафта и позволяет произвести количественную оценку. Многие теоретические методы основываются на теории графов и оценивают структуру ландшафта лишь с математической точки зрения. Ранее в рамках этой теории для оценки степени связанности и фрагментации биотопов использовались только такие показатели, как количество изолированных мест обитания и расстояния между ними. Но с течением времени вводятся новые индексы и показатели, математические вычисления становятся все более сложными, требуется все больше исходных данных. Систематическое усложнение таких методов не только ограничивает их практическое применение [1], но и затрудняет процесс интерпретации результатов [3]. Возникает необходимость в разработке методики для качественного и количественного анализа связанности биотопов, которая не требовала бы большого объема входных данных и сложных математических расчетов и могла бы быть легко адаптирована к местным условиям.
В основу новой методики лег метод, разработанный Кристофером Янгом и Питером Джарвисом [4]. Авторы рассматривают природный каркас города как систему, состоящую из двух основных компонентов – соединительных и площадных мест обитания. Соединительные – линейные по пространственной конфигурации места обитания (например, озелененные улицы, железнодорожные пути, реки и т.п.). Они объединяют изолированные площадные места обитания и обеспечивают потенциальные маршруты для распространения растений и животных. Анализируя картографические данные для заданного участка, авторы выделяют места обитания различных видов. Затем производят подсчет связей между всеми выявленными биотопами. Под связью авторы подразумевают любой прямой контакт между любыми двумя биотопами. Все связи подразделяют на два типа. К первому типу относят связи между двумя площадными местами обитания, остальные связи относят ко второму типу. Коэффициент фрагментации определяют как отношение количества связей второго типа к количеству связей первого типа на заданном участке. Величина коэффициента фрагментации при этом может принять любое неотрицательное значение, поэтому данный метод можно использовать лишь для сравнительного анализа. Авторы также производят качественную оценку связей, которая основывается на натурном анализе исследуемого участка. При этом не приводится какой-либо шкалы для оценки, что делает результаты анализа крайне субъективными.
При разработке новой методики также использовался коэффициент площади биотопа (BAF) – отношение экологически эффективных площадей к общей площади объекта [5]. В отличие от многих аналогов, при расчете BAF во внимание берутся все площади, которые оказывают положительный эффект на экосистему. Для расчета BAF разработана таблица весовых коэффициентов для различных элементов городского ландшафта (табл. 1). При этом расчетные веса варьируют в зависимости от эвапотранспирационных качеств, водопроницаемости, возможности задерживать дождевую воду и от степени значимости для растительных и животных сообществ [6].
Таблица 1
Весовые коэффициенты для расчета коэффициента площади биотопа
|
Тип элемента |
Вес |
Свойства |
Примеры |
|
Непроницаемые поверхности |
0,0 |
Участки с водонепроницаемыми покрытиями, не представляют ценности для растений и животных |
Бетон, асфальт, плиточное покрытие (на монолитном основании или с залитыми швами), водостойкий пластик |
|
Частично проницаемые |
0,3 |
воздухо- и водопроницаемые поверхности, почти не представляют ценности для растений и животных |
Клинкер, плиточное покрытие, брусчатка, уплотненный грунт |
|
Полупроницаемые |
0,5 |
воздухо- и водопроницаемые поверхности, плохие инфильтрационные свойства, пригодны для жизни растений и животных |
Газонная решетка (с развитым травяным покровом) |
|
Участки озеленения на искусственных основаниях, с почвенным слоем толщиной менее 80 см |
0,5 |
Средние или хорошие эвапотранспирационные свойства, плохие инфильтрационные свойства, выполняют пылезащитную функцию, пригодны для жизни растений и животных |
Насаждения на кровле подземной автостоянки (с толщиной почвенного слоя менее 80 см), приподнятые гряды и цветники |
|
Участки озеленения на искусственных основаниях, с почвенным слоем толщиной более 80 см |
0,7 |
Средние или хорошие эвапотранспирационные, плохие инфильтрационные свойства, выполняют пылезащитную функцию, пригодны для жизни растений и животных |
Насаждения на кровле подземной автостоянки (с толщиной почвенного слоя более 80 см) |
|
Участки озеленения на естественном основании |
1 |
Хорошие эвапотранспирационные и инфильтрационные свойства, выполняют пылезащитную функцию, создают благоприятные условия для жизни растений и животных |
|
|
Участки, с которых дождевой сток направляется на растительный покров |
0,2 |
Способствуют восстановлению грунтовых вод |
Кровли |
|
Элементы вертикального озеленения |
0,5 |
Выполняют пылезащитную функцию, создают благоприятные условия для жизни растений и животных |
|
|
Кровельное озеленение |
0,7 |
Хорошие эвапотранспирационные, плохие инфильтрационные свойства, выполняют пылезащитную функцию, пригодны для жизни растений и животных |
Экологически эффективная площадь определяется следующим образом:
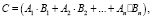 (1)
(1)
где C – экологически эффективная площадь; А1, А2, Аn – площади занятые 1, 2, n элементом; B1, B2, Bn – весовой коэффициент для 1, 2, n типа элемента, определенный по таблице весовых коэффициентов (табл. 1).
Расчет коэффициента площади биотопа производится следующим образом:
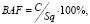 (2)
(2)
где Sq – общая площадь рассматриваемого объекта.
Для систематизации и использования экспериментальных данных на этапе определения необходимого количества эффективных связей использовались методы математической статистики [7]. Из элементов выборки выстраивались вариационные ряды, затем производилась оценка математического ожидания и дисперсии. Далее определялись доверительные интервалы распределения случайной величины с уровнем значимости γ = 0,95.
Результаты исследования и их обсуждение
Разработанный метод основывается на анализе спутниковых снимков. На них выделяются участки размером 1 км×1 км с наиболее характерной для заданной местности пространственной структурой, конфигурацией дорожно-транспортной сети и застройки, долей открытых пространств. Выделенные участки используются для дальнейшего анализа. На первом этапе определяется степень влияния фрагментации ландшафтов на биотопы, на втором – оценивается качество связей между биотопами.
Первый этап. В последнее время научные дебаты относительно фрагментации ландшафтов в основном сосредоточены на вопросе: «Когда последствия фрагментации среды становятся значимыми?». Или, наоборот: «Какая площадь необходима для поддержания жизнеспособности популяций целевых видов?». Некоторые эмпирические исследования показывают, что последствия фрагментации становятся ощутимыми только, когда площадь биотопов уменьшается до 20–30 % [1]. Большинство этих исследований были сфокусированы главным образом на сельскохозяйственных или лесных ландшафтах. Принимая во внимание то, что в агрессивной городской среде большинство организмов уже находится в ослабленном состоянии, негативные эффекты фрагментации ландшафтов, вероятно, имеют здесь более серьезные последствия для организмов даже при больших площадях биотопов. Поэтому для данной методики минимальное значение коэффициента площади биотопов, необходимое для поддержания биоразнообразия, принимается равным 30 %.
В ходе дешифрирования на каждом спутниковом снимке определяются различные типы покрытий и высчитывается общая площадь для каждого из них. Далее определяется коэффициент площади биотопа (2).
Многие ученые считают, что разного рода коридоры между изолированными местами обитания способны смягчить негативные эффекты фрагментации [8; 9]. Однако тот факт, что коридор существует, не говорит о том, что он используется. В некоторых случаях коридоры могут даже служить барьером. Поэтому при низких значениях BAF (менее 30 %) необходимо выяснить, существуют ли связи между фрагментами ландшафта и насколько эффективно эти связи функционируют. Для этого переходят ко второму этапу анализа.
Второй этап. Для качественной оценки связей между фрагментами ландшафта по снимкам определяются различные виды местообитаний (по методу Янга и Джарвиса). Каждая связь между биотопами рассматривается индивидуально и признается либо эффективной, либо неэффективной (рис. 1). Так как свойства местообитаний могут быть неоднородными по площади, при оценке качества связи следует анализировать участки, прилегающие непосредственно к месту контакта. Для оценки эффективности связи используется балльная система (табл. 2). Для каждой связи рассчитывается общий балл, находящийся в диапазоне от 0 до 11. Если общий балл меньше или равен 5, связь признается эффективной.
Таблица 2
Критерии для оценки эффективности связи между биотопами в Санкт-Петербурге
|
Критерий |
Балл |
|
Интенсивное движение автотранспорта |
2 |
|
Плохая циркуляция воздуха |
2 |
|
Значение BAF ниже 10 % |
2 |
|
Наличие физических барьеров |
2 |
|
Высокая механическая нагрузка |
2 |
|
Нарушение светового режима |
1 |

Рис. 1. Выделение различных видов биотопов и оценка качества связей между ними
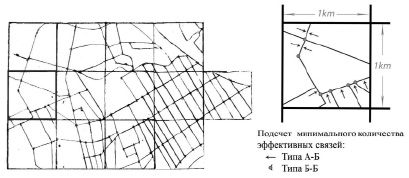
Рис. 2. Анализ снимков для определения необходимого количества эффективных связей каждого типа
Необходимое количество эффективных связей. Для определения необходимого количества эффективных связей каждого типа были проанализированы другие 77 снимков площадью 1 км2. Для этого на каждом снимке выделялись площадные (А) и соединительные (Б) биотопы. Затем для каждого снимка составлялась схема, на которой отображались выявленные биотопы (рис. 2). На схеме графическим путем определялось минимальное количество связей каждого типа, необходимое для того, чтобы сформировать из биотопов единую систему (рис. 2). Далее вычислялось отношение минимально необходимого количества связей каждого типа к общему числу связей этого типа для каждого из снимков. В результате статистического анализа данных, полученных при исследовании 76 снимков, выяснилось, что в 95 % случаев для формирования единой системы биотопов необходимо, чтобы не менее 69,5–78,8 % связей типа Б-Б и не менее 40,3–43,1 % связей типа А-Б были эффективными (табл. 3). При этом эффективность связей типа А-А не влияет на общую ситуацию.
Таблица 3
Расчет необходимого количества эффективных связей
|
Снимок, № п/п |
Кол-во биотопов |
Кол-во связей |
Минимальное кол-во эффективных связей |
Доля необходимых эффективных связей от общего числа связей, % |
Доля всех необходимых эффективных связей от общего числа связей, % |
||||||||
|
Тип А |
Тип Б |
Тип А-А |
Тип Б-Б |
Тип А-Б |
Всего |
Тип А-А |
Тип Б-Б |
Тип А-Б |
Тип А-А |
Тип Б-Б |
Тип А-Б |
||
|
1 |
6 |
5 |
0 |
4 |
14 |
18 |
0 |
3 |
7 |
0,0 |
75,0 |
50,0 |
55,6 |
|
2 |
5 |
4 |
0 |
3 |
10 |
13 |
0 |
3 |
5 |
0,0 |
100,0 |
50,0 |
61,5 |
|
3 |
6 |
5 |
0 |
3 |
11 |
14 |
0 |
3 |
5 |
0,0 |
100,0 |
45,5 |
57,1 |
|
4 |
6 |
5 |
0 |
3 |
13 |
16 |
0 |
2 |
6 |
0,0 |
66,7 |
46,2 |
50,0 |
|
5 |
6 |
4 |
0 |
3 |
14 |
17 |
0 |
2 |
6 |
0,0 |
66,7 |
42,9 |
47,1 |
|
6 |
7 |
6 |
0 |
4 |
17 |
21 |
0 |
4 |
8 |
0,0 |
100,0 |
47,1 |
57,1 |
|
7 |
6 |
4 |
0 |
3 |
14 |
17 |
0 |
3 |
6 |
0,0 |
100,0 |
42,9 |
52,9 |
|
8 |
7 |
5 |
0 |
4 |
14 |
18 |
0 |
3 |
8 |
0,0 |
75,0 |
57,1 |
61,1 |
|
9 |
4 |
3 |
0 |
2 |
16 |
18 |
0 |
2 |
4 |
0,0 |
100,0 |
25,0 |
33,3 |
|
10 |
7 |
4 |
1 |
2 |
13 |
16 |
0 |
2 |
7 |
0,0 |
100,0 |
53,8 |
56,3 |
|
11 |
5 |
5 |
0 |
4 |
12 |
16 |
0 |
2 |
5 |
0,0 |
50,0 |
41,7 |
43,8 |
|
12 |
6 |
5 |
0 |
3 |
15 |
18 |
0 |
3 |
6 |
0,0 |
100,0 |
40,0 |
50,0 |
|
13 |
11 |
9 |
0 |
10 |
28 |
38 |
0 |
6 |
11 |
0,0 |
60,0 |
39,3 |
44,7 |
|
14 |
10 |
7 |
2 |
3 |
17 |
22 |
0 |
2 |
10 |
0,0 |
66,7 |
58,8 |
54,5 |
|
15 |
10 |
8 |
0 |
9 |
26 |
35 |
0 |
4 |
12 |
0,0 |
44,4 |
46,2 |
45,7 |
|
16 |
10 |
7 |
0 |
9 |
29 |
38 |
0 |
4 |
9 |
0,0 |
44,4 |
31,0 |
34,2 |
|
17 |
15 |
11 |
0 |
9 |
46 |
55 |
0 |
9 |
15 |
0,0 |
100,0 |
32,6 |
43,6 |
|
18 |
13 |
10 |
0 |
11 |
39 |
50 |
0 |
8 |
14 |
0,0 |
72,7 |
35,9 |
44,0 |
|
19 |
7 |
4 |
0 |
4 |
17 |
21 |
0 |
4 |
7 |
0,0 |
100,0 |
41,2 |
52,4 |
|
20 |
7 |
4 |
0 |
4 |
16 |
20 |
0 |
4 |
6 |
0,0 |
100,0 |
37,5 |
50,0 |
|
21 |
10 |
5 |
0 |
5 |
26 |
31 |
0 |
5 |
10 |
0,0 |
100,0 |
38,5 |
48,4 |
|
22 |
8 |
6 |
0 |
5 |
23 |
28 |
0 |
5 |
8 |
0,0 |
100,0 |
34,8 |
46,4 |
|
23 |
10 |
9 |
0 |
7 |
29 |
36 |
0 |
7 |
10 |
0,0 |
100,0 |
34,5 |
47,2 |
|
24 |
7 |
4 |
0 |
4 |
14 |
18 |
0 |
4 |
7 |
0,0 |
100,0 |
50,0 |
61,1 |
|
25 |
8 |
4 |
0 |
4 |
26 |
30 |
0 |
3 |
9 |
0,0 |
75,0 |
34,6 |
40,0 |
|
26 |
12 |
7 |
0 |
10 |
33 |
43 |
0 |
6 |
12 |
0,0 |
60,0 |
36,4 |
41,9 |
|
27 |
5 |
3 |
0 |
2 |
11 |
13 |
0 |
2 |
5 |
0,0 |
100,0 |
45,5 |
53,8 |
|
28 |
4 |
3 |
0 |
2 |
8 |
10 |
0 |
2 |
4 |
0,0 |
100,0 |
50,0 |
60,0 |
|
29 |
10 |
6 |
0 |
6 |
25 |
31 |
0 |
4 |
11 |
0,0 |
66,7 |
44,0 |
48,4 |
|
30 |
12 |
9 |
0 |
10 |
31 |
41 |
0 |
6 |
12 |
0,0 |
60,0 |
38,7 |
43,9 |
|
31 |
14 |
9 |
3 |
10 |
34 |
47 |
0 |
6 |
16 |
0,0 |
60,0 |
47,1 |
46,8 |
|
32 |
9 |
9 |
0 |
9 |
26 |
35 |
0 |
5 |
10 |
0,0 |
55,6 |
38,5 |
42,9 |
|
33 |
10 |
9 |
0 |
9 |
25 |
34 |
0 |
6 |
13 |
0,0 |
66,7 |
52,0 |
55,9 |
|
34 |
11 |
9 |
0 |
10 |
27 |
37 |
0 |
6 |
10 |
0,0 |
60,0 |
37,0 |
43,2 |
|
35 |
18 |
10 |
0 |
13 |
56 |
69 |
0 |
8 |
26 |
0,0 |
61,5 |
46,4 |
49,3 |
|
36 |
16 |
9 |
0 |
13 |
47 |
60 |
0 |
6 |
22 |
0,0 |
46,2 |
46,8 |
46,7 |
|
37 |
8 |
6 |
0 |
5 |
18 |
23 |
0 |
4 |
8 |
0,0 |
80,0 |
44,4 |
52,2 |
|
38 |
16 |
8 |
0 |
13 |
48 |
61 |
0 |
8 |
18 |
0,0 |
61,5 |
37,5 |
42,6 |
|
39 |
17 |
13 |
0 |
18 |
54 |
72 |
0 |
11 |
19 |
0,0 |
61,1 |
35,2 |
41,7 |
|
40 |
17 |
10 |
0 |
12 |
50 |
62 |
0 |
7 |
24 |
0,0 |
58,3 |
48,0 |
50,0 |
|
41 |
10 |
8 |
0 |
8 |
28 |
36 |
0 |
5 |
12 |
0,0 |
62,5 |
42,9 |
47,2 |
|
42 |
6 |
5 |
0 |
5 |
13 |
18 |
0 |
3 |
5 |
0,0 |
60,0 |
38,5 |
44,4 |
|
43 |
11 |
7 |
0 |
8 |
29 |
37 |
0 |
5 |
12 |
0,0 |
62,5 |
41,4 |
45,9 |
|
44 |
10 |
7 |
0 |
10 |
27 |
37 |
0 |
4 |
12 |
0,0 |
40,0 |
44,4 |
43,2 |
|
45 |
9 |
8 |
0 |
8 |
26 |
34 |
0 |
6 |
10 |
0,0 |
75,0 |
38,5 |
47,1 |
|
46 |
9 |
8 |
0 |
7 |
25 |
32 |
0 |
6 |
9 |
0,0 |
85,7 |
36,0 |
46,9 |
|
Окончание табл. 3 |
|||||||||||||
|
Снимок, № п/п |
Кол-во биотопов |
Кол-во связей |
Минимальное кол-во эффективных связей |
Доля необходимых эффективных связей от общего числа связей, % |
Доля всех необходимых эффективных связей от общего числа связей, % |
||||||||
|
Тип А |
Тип Б |
Тип А-А |
Тип Б-Б |
Тип А-Б |
Всего |
Тип А-А |
Тип Б-Б |
Тип А-Б |
Тип А-А |
Тип Б-Б |
Тип А-Б |
||
|
47 |
11 |
7 |
0 |
6 |
29 |
35 |
0 |
5 |
11 |
0,0 |
83,3 |
37,9 |
45,7 |
|
48 |
5 |
3 |
0 |
2 |
11 |
13 |
0 |
2 |
5 |
0,0 |
100,0 |
45,5 |
53,8 |
|
49 |
6 |
4 |
0 |
5 |
12 |
17 |
0 |
2 |
6 |
0,0 |
40,0 |
50,0 |
47,1 |
|
50 |
22 |
14 |
0 |
22 |
72 |
94 |
0 |
12 |
25 |
0,0 |
54,5 |
34,7 |
39,4 |
|
51 |
11 |
9 |
0 |
10 |
35 |
45 |
0 |
5 |
12 |
0,0 |
50,0 |
34,3 |
37,8 |
|
52 |
6 |
4 |
0 |
3 |
13 |
16 |
0 |
3 |
6 |
0,0 |
100,0 |
46,2 |
56,3 |
|
53 |
26 |
12 |
0 |
21 |
84 |
105 |
0 |
13 |
30 |
0,0 |
61,9 |
35,7 |
41,0 |
|
54 |
6 |
5 |
0 |
7 |
17 |
24 |
0 |
3 |
6 |
0,0 |
42,9 |
35,3 |
37,5 |
|
55 |
6 |
6 |
0 |
4 |
16 |
20 |
0 |
2 |
6 |
0,0 |
50,0 |
37,5 |
40,0 |
|
56 |
14 |
8 |
0 |
12 |
37 |
49 |
0 |
6 |
17 |
0,0 |
50,0 |
45,9 |
46,9 |
|
57 |
7 |
7 |
0 |
6 |
14 |
20 |
0 |
2 |
5 |
0,0 |
33,3 |
35,7 |
35,0 |
|
58 |
9 |
5 |
0 |
5 |
24 |
29 |
0 |
4 |
10 |
0,0 |
80,0 |
41,7 |
48,3 |
|
59 |
6 |
4 |
0 |
2 |
12 |
14 |
0 |
2 |
5 |
0,0 |
100,0 |
41,7 |
50,0 |
|
60 |
7 |
6 |
0 |
6 |
16 |
22 |
0 |
4 |
6 |
0,0 |
66,7 |
37,5 |
45,5 |
|
61 |
6 |
5 |
0 |
5 |
15 |
20 |
0 |
3 |
6 |
0,0 |
60,0 |
40,0 |
45,0 |
|
62 |
8 |
5 |
0 |
5 |
19 |
24 |
0 |
3 |
9 |
0,0 |
60,0 |
47,4 |
50,0 |
|
63 |
5 |
6 |
0 |
4 |
13 |
17 |
0 |
2 |
6 |
0,0 |
50,0 |
46,2 |
47,1 |
|
64 |
5 |
3 |
0 |
2 |
11 |
13 |
0 |
2 |
5 |
0,0 |
100,0 |
45,5 |
53,8 |
|
65 |
9 |
7 |
0 |
7 |
24 |
31 |
0 |
4 |
10 |
0,0 |
57,1 |
41,7 |
45,2 |
|
66 |
6 |
4 |
0 |
1 |
11 |
12 |
0 |
1 |
4 |
0,0 |
100,0 |
36,4 |
41,7 |
|
67 |
8 |
6 |
0 |
6 |
21 |
27 |
0 |
4 |
8 |
0,0 |
66,7 |
38,1 |
44,4 |
|
68 |
5 |
3 |
0 |
1 |
10 |
11 |
0 |
1 |
4 |
0,0 |
100,0 |
40,0 |
45,5 |
|
69 |
8 |
5 |
0 |
4 |
19 |
23 |
0 |
3 |
8 |
0,0 |
75,0 |
42,1 |
47,8 |
|
70 |
7 |
4 |
0 |
4 |
18 |
22 |
0 |
3 |
8 |
0,0 |
75,0 |
44,4 |
50,0 |
|
71 |
9 |
9 |
0 |
8 |
30 |
38 |
0 |
5 |
10 |
0,0 |
62,5 |
33,3 |
39,5 |
|
72 |
9 |
7 |
0 |
6 |
22 |
28 |
0 |
6 |
9 |
0,0 |
100,0 |
40,9 |
53,6 |
|
73 |
9 |
6 |
0 |
6 |
24 |
30 |
0 |
5 |
10 |
0,0 |
83,3 |
41,7 |
50,0 |
|
74 |
3 |
2 |
0 |
1 |
4 |
5 |
0 |
1 |
2 |
0,0 |
100,0 |
50,0 |
60,0 |
|
75 |
8 |
6 |
0 |
9 |
20 |
29 |
0 |
5 |
8 |
0,0 |
55,6 |
40,0 |
44,8 |
|
76 |
7 |
3 |
0 |
3 |
16 |
19 |
0 |
3 |
6 |
0,0 |
100,0 |
37,5 |
47,4 |
|
Выборочное среднее |
– |
74,2 |
41,7 |
47,7 |
|||||||||
|
Выборочная дисперсия |
– |
429,1 |
37,9 |
40,1 |
|||||||||
|
Верхняя граница доверительного интервала |
– |
78,8 |
43,1 |
49,1 |
|||||||||
|
Нижняя граница доверительного интервала |
– |
69,5 |
40,3 |
46,2 |
|||||||||
Таким образом, если на втором этапе анализа выясняется, что доля эффективных связей типа Б-Б ниже 69,5 %, и/или доля эффективных связей типа А-Б ниже 40,3 %, делается вывод о том, что степень связанности ландшафтов низкая. В таком случае существующих связей недостаточно, чтобы поддержать нормальное функционирование биотопов на заданном участке.
Методика была апробирована на примере города Санкт-Петербурга [10] и доказала простоту и эффективность использования.
Выводы
Основой предлагаемой авторами методики является метод, разработанный Кристофером Янгом и Питером Джарвисом, которые рассматривают зеленую инфраструктуру города как систему, состоящую из двух основных элементов – площадных и линейных (соединительных) объектов. При разработке новой методики также использовался коэффициент площади биотопа (BAF): отношение экологически эффективных площадей к общей площади объекта.
На спутниковых снимках с наиболее характерной для заданной местности пространственной структурой, конфигурацией дорожно-транспортной сети и застройки, долей открытых пространств выделялись участки размером 1 км × 1 км. На выделенных участках осуществлялся двухэтапный анализ. Степень влияния фрагментации ландшафтов на биотопы оценивалась на первом этапе, качество связей между биотопами анализировалась на втором.
В результате разработанная методика позволяет провести комплексную оценку связанности ландшафтов с минимальным количеством исходных данных, что облегчает интерпретацию результатов и расширяет возможности практического применения. При этом методика может быть легко адаптирована к местным условиям за счет изменения критериев для оценки эффективности связей, уменьшения или увеличения размеров и разрешения спутниковых снимков. Для увеличения точности вычислений спутниковые снимки можно заменить материалами топографической съемки.



