В настоящее время разработаны математические модели, которые широко используются для воспроизведения термогидродинамики озер, такие как POM, NEMO [1], ECOM, ELCOM и другие [2–4], в том числе и для моделирования ледовых явлений. Однако перечисленные модели сложны и не обладают достаточной гибкостью в адаптации к конкретным озерам, а также требуют сбора большого количества разнообразной исходной информации, что затрудняет их использование при моделировании и прогнозировании ледовитости озер.
Для прогнозирования временных рядов, в том числе показателя ледовитости озер, могут применяться статистические методы, основанные на применении вероятностных моделей, таких как регрессионные, авторегрессионные (ARIMAX, ARHCH), экспоненциального сглаживания и другие [5]. Данные методы просты, поскольку для их применения не нужно математическое описание происходящих физических процессов в озере. Однако перечисленные методы не предназначены для моделирования нелинейных процессов, поскольку дают большие погрешности. Поэтому они являются непригодными для прогнозирования ледовитости озер.
Для решения задач, связанных с прогнозированием нелинейных процессов, хорошие результаты на основе некоторой обучающей выборки показывают искусственные нейронные сети [6]. Преимуществами данного метода является гибкость, адаптивность, простота применения, высокая точность прогноза.
В связи с этим целью данного исследования является обоснование параметров многослойных персептронов (являются частным случаем искусственной нейронной сети прямого распространения) для прогнозирования ледовитости озер на примере Онежского озера. Основными задачами исследования являются:
1. Формирование обучающих и контрольных выборок на основе суточных рядов показателей ледовитости Онежского озера за периоды 2004–2016 гг. и 2016–2017 гг. соответственно.
2. Выбор оптимальной архитектуры и параметров многослойных персептронов для прогнозирования ледовитости Онежского озера и их обучение.
3. Тестирование обученных персептронов, а также статистических методов прогнозирования на контрольных выборках в сравнении с фактическими значениями ледовитости.
Материалы и методы исследования
Ледовый режим озер, как правило, состоит из трех фаз: замерзание, ледостав, вскрытие, на каждой из которых динамика значений ледовитости имеет свои особенности (рост, снижение или стагнация значений). В данном исследовании рассматривались две фазы ледового режима: замерзание и вскрытие, поскольку в фазу ледостава площадь ледовых образований практически не изменяется. Причем обоснование параметров персептронов для прогнозирования ледовитости осуществлялось отдельно для каждой рассматриваемой фазы ледового режима. Это позволило существенно оптимизировать процесс обучение каждого персептрона.
В качестве натурной основы для получения суточных рядов показателей ледовитости Онежского озера использован банк данных спутниковых наблюдений (платформы AQUA, TERRA, NOAA – 14,15,16,17,18, GOES – 9,10,11,13 и др.) о ледовой обстановке северного полушария с пространственным разрешением 4 км. Наблюдения в данном режиме ведутся с 2004 г. по настоящее время с временным шагом – 1 день (http://nsidc.org/data/G02156). В результате автоматизированного анализа [7] используемых спутниковых данных с идентификацией координат акватории Онежского озера рассчитаны значения ледовитости за каждый день периода 2004–2017 гг. (рис. 1), а также разделены по фазам ледового режима.
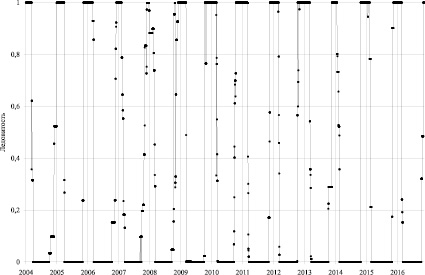
Рис. 1. Ледовитость Онежского озера по данным спутниковых наблюдений за период 2004–2017 гг.
По рис. 1 можно заключить, что Онежское озеро ежегодно полностью покрывается льдом и полностью освобождается от него, в связи с чем поведение функции ледовитости от времени fice(t) имеет циклический характер с предельными значениями от 0 до 1. Такое поведение функции fice(t) позволяет избежать нормирования входных и выходных сигналов персептронов, обусловленных значениями ледовитости озера.
Общий алгоритм работы персептронов для прогнозирования ледовитости озер
В настоящем исследовании использовались многослойные персептроны с одним скрытым слоем без смещения (рис. 2). Архитектура таких персептронов представлена тремя слоями: входной слой с числом нейронов (m), скрытый слой с числом нейронов (n) и выходной слой с числом нейронов (p).
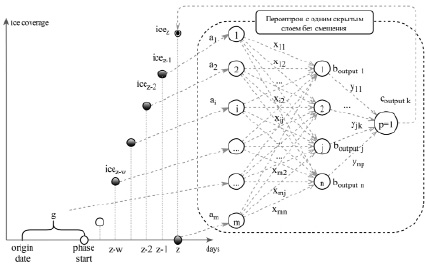
Рис. 2. Схема применения многослойного персептрона для прогнозирования ледовитости озер на основе предшествующих значений
Работа многослойных персептронов заключается в передаче сигналов от нейронов предыдущего слоя к нейронам последующего посредством синаптических связей, которые имеют определенные веса, разные для каждой пары нейронов. Общий алгоритм работы нейронной сети данного типа заключается в следующем (рис. 2):
1. На входные нейроны поступает сигнал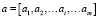 
. Посредством установленных весов синаптических связей сигналы от каждого входного нейрона преобразуются, суммируются и подаются в нейроны скрытого слоя в качестве входного сигнала: 
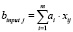, где 
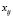– вес синаптической связи между i-м нейроном входного слоя и j-м нейроном скрытого слоя, 
, 
.
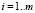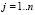2. В каждом нейроне скрытого слоя сигнал преобразуется посредством активационной функции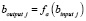 
. Аналогичным образом сигналы от нейронов скрытого слоя преобразуются, суммируются и подаются нейронам последующего (выходного) слоя: 
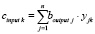, где 
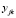– вес синаптической связи между j-м нейроном скрытого слоя и k-м нейроном выходного слоя, 
.
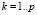3. В каждом нейроне выходного слоя сигнал преобразуется активационной функцией: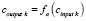 
. Далее результат интерпретируется.
Алгоритм и параметры обучения многослойных персептронов для прогнозирования ледовитости озер
Обучение многослойных персептронов в данном исследовании осуществлялось методом обратного распространения ошибки с использованием учителя [8]. Метод обратного распространения ошибки предполагает использование некоторой обучающей выборки, состоящей из набора тренировочных сетов (входных и соответствующих им выходных сигналов). При этом для обучения формируются тренировочные эпохи, которые включают тренировочные сеты данной выборки, перемешанные случайным образом для каждой эпохи. Процесс обучения персептронов осуществляется в несколько тренировочных эпох, для каждой из которых выполняется несколько итераций. Число итераций соответствует числу тренировочных сетов, входящих в состав тренировочной эпохи. Каждая итерация включает в себя следующие процедуры:
1. Из тренировочной эпохи выбирается тренировочный сет, который состоит из массива входных сигналов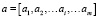 
и массива целевых значений (учителя) 
.
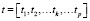2. Для каждого нейрона выходного слоя рассчитываются значения выходного сигнала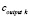 
, а также локальный градиент по формуле 
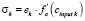, где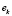 
– сигнал ошибки, вычисляется по формуле: 
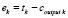. Помимо этого вычисляется величина корректировки веса синаптической связи: 
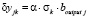, где α – скорость обучения персептрона.
3. Для каждого нейрона скрытого слоя рассчитывается локальный градиент по формуле: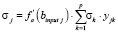 
, а также величина корректировки веса синаптической связи: 
.
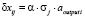4. Вес каждой синаптической связи персептрона изменяется за счет прибавления соответствующего корректировочного значения: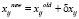 
, 
.
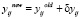После прохождения каждого тренировочного сета в процессе обучения персептрона рассчитывалась среднеквадратическая ошибка отклика по отношению к учителю MSE. Для каждой тренировочной эпохи рассчитывалось среднее арифметическое значение среднеквадратических ошибок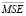 
. Критерием останова обучения являлось условие [6]:
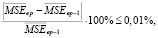
где ep – номер текущей тренировочной эпохи.
Скорость обучения α выбрана опытным путем: α = 0,001.
Начальные веса синаптических связей нейронов выбирались случайным образом из равномерного распределения с математическим ожиданием, равным 0, и дисперсией, которая определяется формулой [8]: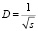 
, где s – количество синаптических связей нейрона. С учетом формулы дисперсии равномерного распределения: 
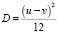, где u, v – соответственно верхняя и нижняя границы интервала, а также с учетом того, что математическое ожидание равно 0, интервал имеет следующий вид: 
.
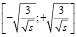Формирование обучающих и контрольных выборок
Тренировочные сеты в виде входных и соответствующих им выходных сигналов формировались в обучающие выборки отдельно для фаз замерзания и вскрытия на основе суточного ряда показателя ледовитости Онежского озера за период 2004–2016 гг.
Наряду с обучающими выборками формировались контрольные выборки отдельно для фаз замерзания и вскрытия, которые также включали входные и соответствующие им выходные сигналы, основанные на суточном ряде показателя ледовитости Онежского озера за период 2016–2017 гг.
В настоящем исследовании в качестве входных сигналов принимались значения ледовитости, предшествующие прогнозируемому значению icez, где z – порядковый номер дня с момента начала рассматриваемой фазы ледового режима, на который выполняется прогноз (рис. 2). Корреляционный анализ суточного ряда показателя ледовитости Онежского озера за период 2004–2016 гг. показал сильную связь (коэффициент парной корреляции r = 0,7–0,92) между значениями icez-d и icez, где d – число дней, предшествующее прогнозируемому дню (d = 1–9). Также установлено, что порядковый номер дня с момента начала рассматриваемой фазы ледового режима является так же значимым фактором (сила корреляционной связи составляет: в фазу замерзания r = 0,32...0,9, в фазу вскрытия r = –0,55…–0,96). Помимо этого установлено, что длительность временного интервала g между некой фиксированной датой origin date и началом фазы phase start (рис. 2) имеет значимую корреляционную связь с длительностью фазы: для фазы замерзания r = –0,56, для фазы вскрытия r = –0,94. В данном исследовании фиксированная дата origin date соответствует самому раннему за период 2004–2016 гг. началу фазы ледового режима Онежского озера: для фазы замерзания – 9 ноября, для фазы вскрытия – 28 февраля.
При этом для оптимальной работы персептронов все входные сигналы должны быть нормализованы в промежутке [0; 1]. Значения ледовитости удовлетворяют условию нормализации, а входной сигнал, соответствующий порядковому номеру дня от момента начала рассматриваемой фазы ледового режима z, в данном исследовании нормировался соотношением
,
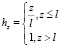где l – максимальное значение длительности рассматриваемой фазы ледового режима за имеющийся временной период, в днях (для фаз замерзания и вскрытия Онежского озера за период 2004–2016 гг. составляет 80 и 71 день соответственно).
Входной сигнал, соответствующий длительности временного интервала g, также нормировался соотношением
,
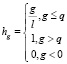где q – максимальное значение длительности временного интервала g для рассматриваемой фазы за имеющийся временной период (для фаз замерзания и вскрытия Онежского озера за период 2004–2016 гг. составляет 56 и 81 день соответственно).
Таким образом, массив входных сигналов имеет вид
,
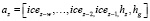где ice – значение ледовитости озера; w – количество значений ледовитости, предшествующих прогнозируемому значению и подаваемых на вход искусственной нейронной сети (рис. 2). В данном исследовании w принималось равным 1, поскольку согласно эвристическим рекомендациям по улучшению работы сети, входные переменные должны быть не коррелированы [8]. В случае же с предшествующими значениями присутствует сильная корреляционная связь между значениями icez-d-1 и icez-d (r > 0,9).
Массив выходных сигналов содержит прогнозируемое значение ледовитости на соответствующий день с момента начала фазы z и имеет вид
.
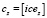Выбор параметров и архитектуры многослойных персептронов
Активационная функция подбиралась опытным путем. Наилучшие результаты при обучении персептронов показала функция гиперболического тангенса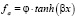 
с параметрами φ = 1,7159, β = 2/3.
Количество нейронов входного слоя в данном исследовании определялось соотношением: m = w + 2 = 3. Количество нейронов выходного слоя обусловлено одним прогнозируемым значением ледовитости: p = 1. Количество нейронов скрытого слоя устанавливалось экспериментально в несколько шагов. На первом шаге обучался персептрон с наиболее простой архитектурой (3–2–1). На каждом последующем шаге обучался персептрон, который имел на один скрытый нейрон больше, чем персептрон на предыдущем шаге. При этом на каждом шаге рассчитывалось значение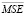 
для последней тренировочной эпохи. Если на текущем шаге данное значение было меньше, чем на предыдущем шаге, то выполнялся следующий шаг, в противном случае – процедура выбора оптимальной архитектуры персептрона заканчивалась, при этом выбирался персептрон, обучавшийся на предыдущем шаге. На рис. 3 представлены графики зависимости 
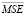от номера тренировочной эпохи для персептронов с разным количеством нейронов в скрытом слое.
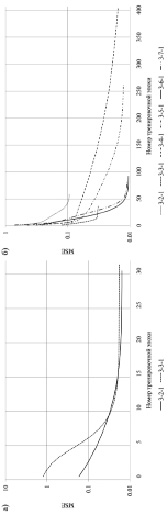
Рис. 3. Графики зависимости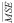 
от номера тренировочной эпохи при обучении для персептронов с разным количеством нейронов в скрытом слое: а) фаза замерзания; б) фаза вскрытия
Наименьшие значения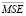 
в последней тренировочной эпохе при обучении показали персептроны с архитектурами: 3–2–1 – в фазу замерзания (
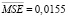), 3–6–1 – в фазу вскрытия (
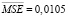). Данные персептроны были выбраны для тестирования на контрольных выборках.
Результаты исследования и их обсуждение
Результаты тестирования персептронов с архитектурами 3–2–1 и 3–6–1 на контрольных выборках в сравнении с фактическими значениями представлены на рис. 4, а также показаны результаты прогнозирования различными статистическими методами: линейная регрессия, скользящее среднее, авторегрессии первого и второго порядков.
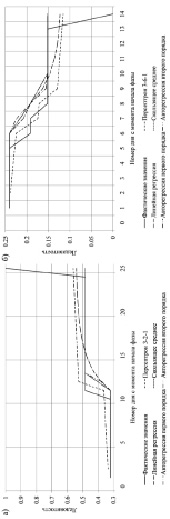
Рис. 4. Прогнозируемые и фактические значения ледовитости Онежского озера за период 2015–2016 гг. (контрольные выборки): а) фаза замерзания; б) фаза вскрытия
Статистический анализ результатов тестирования (среднеквадратическая ошибка прогнозируемых и фактических значений MSE, среднее значение абсолютных отклонений прогнозируемых и фактических значений MAD, максимальное абсолютное отклонение прогнозируемых и фактических значений Δmax) различных методов прогнозирования ледовитости на контрольных выборках представлен в таблице.
Результаты тестирования методов прогнозирования ледовитости на контрольных выборках
|
Методы прогнозирования |
Фаза замерзания |
Фаза вскрытия |
Общие MSE |
||||
|
MSE |
MAD |
Δmax |
MSE |
MAD |
Δmax |
||
|
Персептроны |
0,0108 |
0,065 |
0,439 |
0,0015 |
0,027 |
0,116 |
0,0076 |
|
Линейная регрессия |
0,0117 |
0,051 |
0,459 |
0,0017 |
0,026 |
0,123 |
0,0083 |
|
Скользящее среднее |
0,0130 |
0,033 |
0,516 |
0,0023 |
0,024 |
0,152 |
0,0094 |
|
Авторегрессия первого порядка |
0,0136 |
0,035 |
0,516 |
0,0025 |
0,026 |
0,152 |
0,0099 |
|
Авторегрессия второго порядка |
0,0145 |
0,038 |
0,516 |
0,0028 |
0,028 |
0,152 |
0,0107 |
Более достоверный прогноз ледовитости персептронов на обеих контрольных выборках по отношению к статистическим методам подтверждается наименьшим значением MSE (таблица). Однако следует отметить, что на обеих контрольных выборках значения MAD у статистических методов ниже, чем для персептронов. Это связано с тем, что на интервалах линейного поведения функции ледовитости от времени fice(t) статистические методы могут давать более точный прогноз, чем персептроны (абсолютные отклонения прогнозируемых статистическими методами от фактических значений Δ ≈ 0). В особенности это актуально в случае, когда площадь ледовых образований остается постоянной. Однако на интервалах нелинейного поведения функции fice(t) на обеих контрольных выборках статистические методы давали гораздо большие ошибки, чем персептроны. Об этом свидетельствуют максимальные значения абсолютных отклонений прогнозируемых и фактических значений ледовитости Δmax (таблица).
В целом можно заключить, что многослойные персептроны позволяют осуществить более адекватное и надежное прогнозирование значений ледовитости озер, чем статистические методы, особенно когда функция fice(t) ведет себя нелинейно, что является типичной ситуацией в большинстве случаев для озер. При этом на интервалах нелинейного поведения функции fice(t) статистические методы дают неприемлемые ошибки прогноза (Δ > 0,3).
Также следует отметить, что абсолютные отклонения прогнозируемых персептронами и фактических значений ледовитости при значительном изменении ледовитости за короткое время (>0,1/день) также являются не всегда удовлетворительными (Δ > 0,2/день). Для решения этой проблемы необходимо исследовать дополнительные факторы, влияющие на показатель ледовитости озер, такие как, например, температура воздуха, воды, скорость ветра. Включение этих факторов в число входных сигналов персептронов значительно расширит их функционал.
Выводы
В данном исследовании обоснованы параметры и архитектура многослойных персептронов для прогнозирования ледовитости Онежского озера в фазы замерзания и вскрытия. Экспериментально показано, что для прогнозирования ледовитости Онежского озера оптимальным является применение персептронов с архитектурами: 3–3–1 – в фазу замерзания и 3–6–1 – в фазу вскрытия. Эти персептроны показали адекватные результаты при тестировании на контрольных выборках: среднеквадратические ошибки составляют 0,0108 и 0,0015 в фазы замерзания и вскрытия соответственно. В результате тестирования в целом по всем контрольным выборкам было установлено, что по сравнению со статистическими методами персептроны имеют меньшее значение среднеквадратической ошибки прогноза (MSE = 0,0076), а также меньшее значение максимального абсолютного отклонения (Δmax = 0,439). В связи с этим можно заключить, что персептроны позволяют более адекватно прогнозировать показатель ледовитости озер, чем статистические методы.
Работа выполнена при финансовой поддержке гранта Президента РФ для поддержки молодых российских ученых МК-3379.2018.5.