При решении широкого круга задач физики атмосферы и метеорологии необходимо иметь данные о состоянии приземного (в пределах нескольких десятков метров от подстилающей поверхности) слоя атмосферы. В частности, требуется учитывать различные характеристики турбулентных составляющих как температурного, так и ветрового поля. С этой целью обычно используются модельные представления этих характеристик. При этом модели базируются в основном на тех эмпирических данных, которые получены в условиях «классической» («колмогоровской») турбулентности. Однако реальные условия, для которых необходимо решение задач турбулентного тепломассообмена в приземном слое, могут существенно отличаться от «идеальных» [1–3]. Важным параметром при решении этих задач служат масштабы турбулентности температурного поля T и компонентов вектора ветра (продольной U, поперечной V и вертикальной W составляющих). Внешний масштаб турбулентности температурного поля помимо задач физики атмосферы активно используется и в других областях, например в теоретических [4, 5] и прикладных [6–8] проблемах распространения оптических волн в атмосфере. Для оценки масштабов применяются разнообразные методики. В ряде случаев эти методики специально подбираются для решения конкретных задач. Примером может служить обзорная статья [9], ориентированная на решение проблем, связанных с астрономическими наблюдениями. В своих исследованиях мы ориентировались на методику определения внешних масштабов через структурные функции метеорологических величин. Эту методику можно отнести к разряду «классических», поскольку результаты параметризации структурных функций (включая оценки масштабов турбулентности) являются основой многочисленных практических приложений. Однако неучет некоторых деталей ее применения может привести к существенным неточностям определения внешних масштабов.
Цель исследования: уточнение методики определения внешних масштабов турбулентности, основанной на анализе структурных функций исследуемых метеорологических величин.
Материалы и методы исследования
Структурная функция (СФ) какого-либо скалярного метеорологического параметра X может быть записана в виде [10]
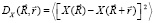, (1)
где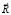 
обозначает точку в пространстве, а 
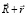– другую (произвольную) точку, отстоящую от первой на расстоянии 
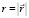. Угловые скобки обозначают усреднение по ансамблю реализаций. В случае, если параметр X относится к классу однородных (локально однородных) и изотропных полей, СФ DX(r) будет зависеть только от модуля сдвига r. Для векторных величин, таких как вектор ветра, следует сформировать структурный тензор, подобный (1), но составленный из компонентов этого вектора. Однако данный аспект проблемы мы не будем рассматривать, поскольку в дальнейшем анализируются отдельные компоненты вектора ветра, выступающие как скалярные величины и формирующие СФ вида (1). Полагая далее, что условия существования СФ метеорологической величины X, заданные в [10], выполнены, запишем ее «классическую» параметризацию в виде
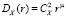, (2)
где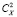 
– структурная характеристика величины X. Размерность 
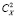должна согласовываться с размерностью X2 и множителя rμ. Параметризация (2), согласно [10], справедлива для пространственных «сдвигов» r в диапазоне 
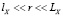, где lX и LX – соответственно внутренний и внешний масштабы турбулентности («инерционный интервал турбулентности»). Вне этого интервала СФ будет иметь иной вид. Важно отметить, что для существования СФ в форме (2) показатель степени μ должен находиться в диапазоне 
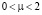[10]. «Классическим» значением, следующим из общей теории турбулентности Колмогорова – Обухова, считается μ = 2/3. В случае однородности поля X структурная функция DX(r) при значениях 
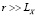будет стремиться к «насыщению» на уровне удвоенной дисперсии 
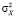величины X и имеет место соотношение [10]
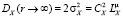. (3)
Если же поле X является локально однородным (например, со стационарными первыми приращениями), то «насыщения» DX(r) не будет [10]. Согласно (3), если известны значения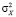 
и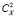 
, то внешний масштаб турбулентности LX может быть определен по формуле
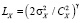, (4)
где показатель степени γ = 1/μ. Не приводя какого-либо дополнительного обзора литературы, отметим, что очень часто как в теоретических выкладках, так и при решении прикладных задач автоматически полагается, что СФ параметризируется в виде (2) и всегда μ = 2/3 ≈ 0,667 (γ = 1,5). Однако СФ метеорологических величин (температуры воздуха, компонентов вектора ветра) далеко не всегда могут быть аппроксимированы с помощью формулы (2). Проведенные нами исследования показали [11–13], что над территориями с усложненной текстурой подстилающей поверхности параметризация СФ в форме (2) является скорее исключением, чем правилом. Не вдаваясь в детали, которые можно узнать в [11–13], укажем, что было выделено три возможных типа СФ, одним из которых является формула (2). В обобщенном виде эти типы можно записать в форме
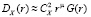, (5)
где безразмерная функция G(r) зависит от типа СФ и равна единице при r = 1 м для любого типа. Область существования СФ в форме (5) ограничивается некоторым сдвигом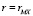 
, при превышении которого формула (5) уже не обеспечивает хорошее качество аппроксимации эмпирической функции DX(r). Структурная функция в форме (5) также подразумевает переход к «насыщению» на уровне 
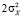при сдвиге r > LX..
С формальной точки зрения можно было бы положить выполнение равенства
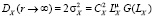(6)
и решить данное уравнение (в общем случае нелинейное) относительно LX. Однако на данном этапе работы мы упростили постановку задачи и использовали для вычисления LX соотношение вида (4), но с показателем степени κ, соответствующим наклону касательной к структурной функции вида (5) в точке r = 1 м:
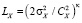. (7)
Нетрудно убедиться, что если СФ вида (5) имеет тип, соответствующий формуле (2), то выполняется равенство γ = κ. Для двух других типов, введенных в [11, 13], γ ≠ κ. В этой связи одной из задач нашей работы являлось определение показателя степени κ, расчет по формуле (7) масштаба LX, вычисление масштаба LXC по формуле (4) при μ = 2/3, оценка различий LX и LXC. Вычисления осуществлялись на основе экспериментальных данных, полученных с помощью ультразвуковых метеостанций (УЗМ) «Метео-2» [14]. Место измерений – большая поляна, окруженная лесопосадками средней высоты (территория обсерватории «БЭК» ИОА СО РАН). Высота размещения измерителя УЗМ – 10 м. Для обработки использовались выборки величин X по времени в некоторой фиксированной точке пространства. Отсчеты при измерениях производились с частотой f ~ 10 Гц. Переход к пространственным координатам подразумевал гипотезу о «замороженной» турбулентности и осуществлялся с использованием формулы r = τVh, где τ – сдвиг во времени при оценках структурной функции, а Vh – средняя скорость ветра на интервале обработки Δt. При этом минимальный сдвиг, с которого могла быть вычислена СФ, составлял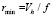 
. В этой связи в обработку не включались эпизоды, когда имели место случаи Vh ≥ 10 м/с. На рис. 1 приведены примеры «эмпирических» структурных функций DT(r) температуры воздуха T, подчиняющихся параметризации (2) (или параметризации (5) при 
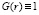) в диапазоне 
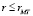. Вычисления DT(r) сделаны по выборкам длительностью Δt = 10 мин. При этом до вычисления СФ из исходных выборок температуры воздуха были удалены скользящие средние данной величины (
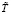), полученные с использованием «временного окна» с размером δt = 2 мин. Фактически, оценка DT(r) проводилась по выборкам случайной величины 
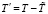, которую мы полагали относящейся к классу стационарных случайных процессов. Такая же предварительная обработка делалась для всех исследовавшихся величин X. Более подробно об использовавшейся процедуре аппроксимации эмпирических структурных функций аналитическими выражениями можно узнать в [11, 13].
Графики функций DT(r) на рис. 1 обозначены цифрами (1, 2, 3). Уровни удвоенных дисперсий, на которых должны «насыщаться» эти СФ, обозначены как 1d, 2d, 3d. Прямые линии, обозначенные как 1k, 2k, 3k, соответствуют случаю «колмогоровской» турбулентности с показателем степени в формуле (2) μ = 2/3. Пересечение данных линий с уровнями, равными удвоенным дисперсиям, отмечено крупными точками. Проекции точек на ось абсцисс дают масштабы турбулентности LTC. Прямые линии, обозначенные как 1e, 2e, 3e, соответствуют аппроксимации эмпирических СФ с «реальным» показателем степени μ. Пересечение этих линий с уровнями, равными удвоенным дисперсиям, отмечено «открытыми» звездочками. Проекции положения звездочек на ось абсцисс дают «истинные» значения масштабов турбулентности LT. Символами «Т» на графиках СФ обозначено завершение интервала, где справедлива аппроксимация (5). Им соответствуют сдвиги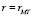 
. Укажем также, что СФ под номером «1» имеет значение μ ≈ 1,141, под номером «2» – μ ≈ 0,667 («классическое» значение), под номером «3» – μ ≈ 0,4. Примеры, приведенные на рис. 1, поясняют ту задачу, которая была поставлена при выполнении данной работы. В частности, для СФ под номером «1» ошибка в оценке внешнего масштаба температурной турбулентности составляет примерно 102 м (LTC ≈ 118 м, LT ≈ 16 м). А для СФ под номером «3» – 3 м (LTC ≈ 3 м, LT ≈ 6 м). Понятно, что использование внешних масштабов турбулентности, вычисленных при «жестком» задании степени μ = 2/3 (γ = 1,5) в формуле (4), может привести к значительным ошибкам в итоговых результатах. Без иллюстраций отметим, что аналогичная ситуация имеет место и для СФ компонентов вектора ветра.
Мы достаточно подробно изложили методические аспекты определения внешних масштабов турбулентности в случае выполнения степенного закона (2) (или (5) при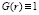 
). Рассмотрим теперь случай, когда функция 
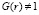(кроме точки r = 1 м). Примеры структурных функций температуры воздуха такого типа приведены на рис. 2. Характерной в данном случае является «параболичность» формы СФ в логарифмических координатах в «инерционном интервале турбулентности», причем «параболичность» может быть как «выпуклой» (график СФ под номером «1»), так и «вогнутой» (график СФ под номером «2»). Обозначения на рис. 2 имеют тот же смысл, что и на рис. 1:
а) цифры с индексом «d» относятся к уровням «насыщения» СФ, равным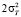 
;
б) цифры с индексом «e» помечают линии, касательные к СФ при r = 1 м;
в) индексом «k» помечены линии с наклоном, соответствующим «колмогоровскому» показателю степени μ = 2/3.
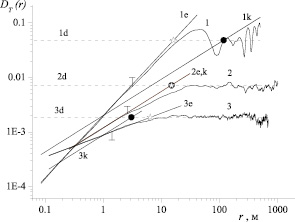
Рис. 1. Примеры структурных функций температуры воздуха, подчиняющихся в «инерционном интервале турбулентности» степенному закону (2)
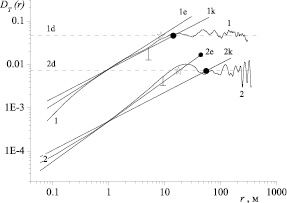
Рис. 2. Примеры структурной функции температуры воздуха, подчиняющейся в «инерционном интервале турбулентности» закону (5)
Координаты символов по оси абсцисс будут соответствовать внешним масштабам турбулентности LT (звездочки) или LTC (точки). Для СФ, помеченной цифрой «1», разность масштабов составляет примерно 5 м, а для СФ с номером «2» – около 34 м.
Приведенные на рис. 1 и 2 примеры достаточно убедительно демонстрируют возможность значительных ошибок в оценках внешних масштабов турбулентности при их определении на основе «колмогоровской» турбулентности (при которой всегда имеет место степенной закон (2) и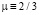 
). В то же время вычисления масштабов по формуле (7) с использованием эмпирических («текущих») значений показателя степени κ обеспечивает вполне адекватные оценки LT, в том числе для случаев, когда структурные функции описываются выражениями вида (5).
Считаем необходимым отметить еще один методический аспект, существенно влияющий на достоверность определения внешних масштабов турбулентности. Он связан с процедурой выделения турбулентных составляющих X' из исходных выборок X. Достаточно часто для получения X' используют формулу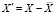 
, где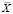 
– среднее арифметическое значение величины X на интервале обработки Δt. Однако даже на относительно коротких интервалах Δt нестационарность X может быть настолько значительной, что турбулентную составляющую X' нельзя отождествлять со стационарным случайным процессом и использовать ее при вычислениях СФ и внешних масштабов турбулентности. Напомним, что в наших вычислениях для выделения турбулентных составляющих используется формула 
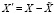, основанная на вычитании скользящего среднего 
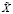, получаемого с применением «временнго окна» δt. Для иллюстрации влияния методики выделения турбулентных составляющих приведем рис. 3, на котором показана суточная развертка масштабов LT, рассчитанных по формуле (7) с применением оценок текущих значений показателя степени κ, масштабов LTC, рассчитанных по формуле (4) с γ = 1,5, и масштабов LTCI, опять-таки рассчитанных по формуле (4) при γ = 1,5, но с выделением турбулентной составляющей температуры с использованием выборочного среднего 
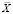. Вычисления проведены при Δt = 10 мин и δt = 2 мин.
Результаты исследования и их обсуждение
Согласно результатам, приведенным на рис. 3, оценки LTCI практически всегда существенно превосходят как LT, так и LTC. Поэтому мы полагаем, что достоверность оценок внешних масштабов турбулентности при выделении пульсационных составляющих с использованием выборочных средних не может быть обеспечена. Без иллюстраций укажем, что подобные результаты имеют место и для внешних масштабов турбулентности компонентов вектора ветра.
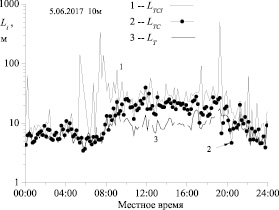
Рис. 3. Внешние масштабы температурной турбулентности, оцененные разными методиками по результатам измерений на высоте 10 м
а б
в г
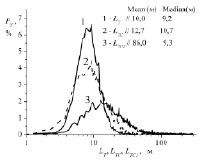
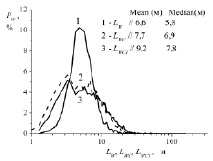
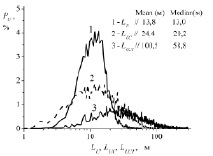
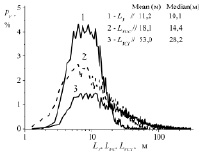
Рис. 4. Эмпирические гистограммы распределения внешних масштабов турбулентности температуры LT, вертикальной LW, продольной LU и поперечной LV составляющих вектора ветра
Отметим также наличие «пропусков» в развертке значений LT. Они связаны с тем, что на отдельных интервалах времени средний квадрат разности исследуемой величины не мог быть аппроксимирован функцией вида (5) с заданной при вычислениях точностью. Требования, устанавливавшиеся при аппроксимации, были достаточно жесткими [11, 13]. При некотором ослаблении этих требований количество «пропусков» должно уменьшиться.
Пример на рис. 3 приводит к выводу, что значительные отклонения LTC и LTCI от LT – это не отдельные случайные эпизоды, а нечто более системное. Подтвердить данный вывод может сравнение статистик LX, LXC и LXCI, полученных по достаточно большому объему экспериментальных данных. На рис. 4 показаны эмпирические гистограммы распределения внешних масштабов всех рассматривавшихся метеорологических параметров PX в процентном выражении, рассчитанные с шагом 0,5 м.
Использованы результаты измерений на высоте 10 м за июнь – июль 2017 г. в пункте наблюдения «БЭК», о котором уже говорилось ранее. Суммарная длительность наблюдений за два указанных месяца составила 851 час, что вполне достаточно для статистической обеспеченности гистограмм (5 105 интервалов по 10 минут с применением δt = 2 мин). На рисунках с гистограммами указаны также средние (mean) и медианные (median) значения внешних масштабов турбулентности LX, LXC и LXCI за обработанный период времени. Очевидно, что статистика масштабов LXC и LXCI заметно отличается от статистики LX, особенно для продольной и поперечной составляющих вектора ветра. Обратим внимание и на то, что статистика масштабов LX стремится к логарифмически нормальному закону распределения.
Заключение
Подводя итог, можно сделать вывод, что для достоверной оценки внешних масштабов турбулентности какой-либо метеорологической величины необходимо по заданному для обработки интервалу времени выделить ее турбулентную составляющую с использованием вычитания из исходной выборки скользящего среднего. После этого следует рассчитать средний квадрат разности исследуемой величины при разных пространственных (временных) сдвигах и аппроксимировать полученную зависимость функцией вида (5) от минимального до максимально возможного сдвига (с заданной точностью). И только после этого приступать к оценкам внешних масштабов турбулентности. В упрощенном виде это обеспечивается формулой (7). Обсуждавшаяся в данной статье методика определения внешних масштабов турбулентности не является «универсальной». Существуют и другие способы определения LX, например, через спектры величин Х или их корреляционные функции. Сопоставление результатов оценок LX разными методиками также вызывает определенный интерес и представляет перспективную задачу.