Очень важными в геофизике являются понятия о прямой и обратной задачах. Прямая задача геофизики сводится к расчету физического поля по известным параметрам возмущающего объекта [1–3]. Параметрами объекта являются: мощность, глубина залегания верхней и нижней кромок, угол падения, намагниченность, плотность и т.п. [1–3]. Прямую задачу геофизики обычно решают на стадии проектирования геофизических работ. Получаемая при этом ожидаемая геофизическая аномалия помогает выбрать соответствующую измерительную аппаратуру и методику наблюдений. Обратная задача геофизики заключается в расчетах параметров и условий залегания аномалии образующего объекта по геофизической аномалии, полученной в результате полевых измерений [1, 2].
Обратная задача геофизики заключается в расчетах параметров аномалиеобразующего объекта по геофизической аномалии, полученной в результате полевых измерений. Ее решают на этапе интерпретации геофизических данных. К сожалению, нередко она может иметь несколько возможных вариантов решения [1].
В данной статье в качестве наблюдаемой аномалии выбрано горизонтальное сдвижение дневной поверхности шахтного поля [4]. В качестве определяемого в ходе решения обратной задачи параметра выбрано определение значения приращения величин равномерно распределенных нагрузок на вертикальных поверхностях модели шахтного поля, что представляет в настоящее время актуальную задачу [5].
Таким образом, по наблюдаемому горизонтальному сдвижению дневной поверхности делается вывод об изменении нагрузок, действующих на периметре модели шахтного поля (на отвесных границах шахтного поля в зависимости от внешних геологических факторов и деятельности человека в непосредственной близости от шахтного поля). Предполагается, что при решении прямой задачи с учетом заданного приращения равномерных нагрузок на отвесных границах шахтного поля в качестве внешних нагрузок будут использованы нормальные давления, последовательно прилагаемые к каждой из боковых поверхностей при закреплении нижней поверхности модели шахтного поля.
Данная задача решается в предположении чисто упругих деформаций породы шахтного поля без учета реологического поведения материала [6, 7].
Методика решения обратной задачи
Методика решения обратной задачи основана на том, что решение задачи теории упругости для твердотельной модели шахтного поля подчиняется принципу суперпозиции. То есть решение для модели шахтного поля может быть представлено набором решений для нагрузок, принятых за единичные на отдельных поверхностях, и отсутствием нагрузок на остальных поверхностях.
Таким образом, методика решения обратной задачи основана на построении набора «реперных» решений прямой задачи. Учитывая многогранную геометрию модели шахтного поля, «реперным» решением будем называть решение прямой задачи, соответствующее приложению среднего, отличного от нуля давления, принятого за единичное, только к одной грани боковой поверхности модели шахтного поля.
Очевидно, что в случае использования гипотезы о линейно-упругом поведении неоднородной в среднем изотропной породы [6, 7] суперпозиция «реперных» решений с искомыми весовыми коэффициентами будет давать измеренные горизонтальные сдвижения дневной поверхности.
Таким образом, решение обратной задачи состоит в определении безразмерных весовых коэффициентов в суперпозиции «реперных» задач. Сами же безразмерные коэффициенты будут определять, во сколько раз реальное приращение давления будет отличаться от принятого за единичное. Количество «реперных» задач определяется количеством боковых вертикальных граней в модели шахтного поля.
Влияние краевых условий на однозначность решения задачи
Одним из основных краевых условий при решении как прямой, так и обратной задачи является то, что предполагается, что основание модели шахтного поля прочно сцеплено с абсолютно твердой и жесткой подстилающей поверхностью.
Это ограничение является существенным и необходимым для того, чтобы построить набор «реперных» решений, так как только оно гарантирует, что модель шахтного поля будет находиться в равновесии под действием равномерно распределенных нагрузок любого типа, приложенных к только одной боковой поверхности шахтного поля.
Таким образом, при жестком закреплении нижней границы модели лидирующими параметрами, определяющими сдвижения дневной поверхности, будут два перемещения в плоскости дневной поверхности (в направлениях 0x и 0y).
Отметим, что если модель шахтного поля представляет из себя ориентированный в декартовой системе параллелепипед, то решение обратной задачи по сдвижению дневной поверхности будет однозначным. В этом случае количество реперных задач будет равно 4, соответственно, количество определяемых параметров (весовых коэффициентов для реперных задач) 4. В этом случае достаточно выбрать две точки на поверхности, в которых заданы по две проекции перемещений в декартовой системе координат, и это даст 4 уравнения для однозначного определения весовых коэффициентов для «реперных» решений, т.е. величин действующих нагрузок на гранях модели шахтного поля.
Однако модель шахтного поля представляет собой прямоугольную призму с неправильным многоугольником в сечении. Соответственно, чтобы получить однозначно разрешимую систему (непереопределенную или недоопределенную) для вычисления весовых коэффициентов необходимо, чтобы количество вертикальных граней призмы (модели шахтного поля) было четным. Тогда для однозначного решения обратной задачи на дневной поверхности достаточно выбрать число индикаторных точек на дневной поверхности равное половине числа вертикальных граней в модели шахтного поля с заданными двумя горизонтальными проекциями перемещений вдоль декартовой системы координат.
Общие сведения по решению обратной задачи для модели шахтного поля
Для демонстрации решения обратной задачи использовалась многослойная модель шахтного поля II и III горизонтов шахтного поля IV РУ ОАО «Беларуськалий» (рис. 1). Нижняя грань модели шахтного поля полностью закреплена. Механические характеристики слоев приведены в таблице.
Механические свойства материалов, использованных при моделировании многослойной структуры модели шахтного поля
|
Порода |
Плотность, кг/м3 |
Модуль Юнга, ГПа |
Коэф. Пуассона |
|
Отложения |
2300 |
0,2 |
0,49 |
|
Глинисто-мергелистая толща |
2200 |
0,7 |
0,35 |
|
Каменная соль |
2300 |
1,64 |
0,29 |
|
Песчаник |
2700 |
35 |
0,19 |
Обоснование выбора программно-аппаратных средств решения обратной задачи
Так как методика решения обратной задачи основана на решении прямых задач, то необходимо остановиться на обосновании использованных при демонстрации методики программных и аппаратных средств решения прямой задачи геомеханики.
Отметим, что при решении серии прямых задач использовалось два пакета со свободной лицензией Code_Aster и Salome во взаимодействии между собой [8, 9].
Code_Aster – пакет для моделирования методом конечных элементов. Разрабатывается в основном компанией EDF (Electricite de France S.A. – крупнейшей энергетической компанией Франции) и первоначально использовался для моделирования узлов и конструкций электростанций, включая атомные. Первая версия была выпущена в 1989 г., в 2001 он был выпущен под открытой лицензией GPL. Данный пакет способен решать задачи термодинамики, механики и ряд смежных, таких как акустика. Решаемые задачи могут быть как линейными, так и нелинейными, статическими и динамическими (имеется explicit решатель). Code_Aster широко используется для решения задач геомеханики и строительства. Имеется широкий выбор моделей материалов для моделирования скальных, осадочных пород и строительных материалов. Пакет сам по себе не имеет графического интерфейса, все управление им выполняется с помощью скриптов и командной строки [8]. Поэтому для подготовки моделей для расчета и анализа полученных материалов следует использовать дополнительное ПО, такое как Salome [9].
Salome – пакет для пре- и постпроцессинга при решении задач методом конечных элементов. Данный пакет предлагает графический интерфейс пользователя, с помощью которого можно создать геометрию модели (для этого имеется полный набор инструментов твердотельного моделирования), построить конечно-элементную сетку, выполнить визуализацию и анализ результатов. Геометрические модели могут получаться из других САПР, Salome поддерживает наиболее распространенные форматы обмена 3D данными [9].
Salome в первую очередь создавался как пакет, обеспечивающий графический интерфейс подготовки моделей и анализа результатов для Code_Aster, но также может использоваться и с другим расчетным ПО, например Elmer или OpenFOAM. Salome также разрабатывается в основном EDF и был выпущен под открытой лицензией GPL в 2001 г.
При расчетах использовалась рабочая станция с характеристиками: 2 процессора Xeon E5-2420 с тактовой частотой 1,9 ГГц, каждый процессор имеет 6 ядер, оперативная память станции четвертого поколения составляет 256 Гб.
Демонстрация методики решения обратной задачи
С помощью указанных программно-аппаратных средств решен набор реперных задач, определяющих горизонтальные перемещения дневной поверхности шахтного поля в выбранных точках поверхности (рис. 1). Предполагалось, что в качестве нагрузок в реперных задачах задавались равномерные по величине давления на боковых поверхностях, равные 105 Па (рис. 2).
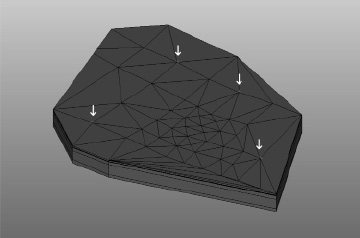
Рис. 1. Выбор индикаторных точек, указанных стрелками, по перемещениям, в которых будет определяться воздействие на боковые поверхности
Для указанных ключевых точек 1–4 (рис. 1) авторами для единичного давления на первой из поверхностей получено решение (UX, UY – значения перемещений вдоль осей 0x и 0y):
.
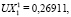
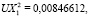
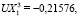
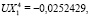
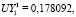
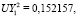
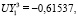
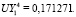Из решений «реперных» краевых задач для семи оставшихся боковых поверхностей с единичными нагрузками совершенно аналогично определяются значения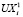 
, 
, 
, 
, 
, 
, 
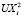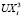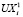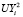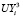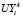(i = 2,8). Далее с помощью полученных решений формируется матрица «жесткости» модели шахтного поля в виде
,
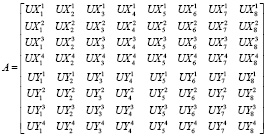которая при численном решении поставленной задачи приобрела следующие значения:
.
Для решения обратной задачи необходимо задать измеренные перемещения индикаторных ключевых точек в виде вектора значений b:
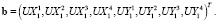
Тогда реальные давления, приложенные к боковым граням, определяемые вектором безразмерных коэффициентов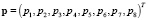 
, измеряемых в долях от принятого за единицу давления 105 Па, будут определяться из решения системы линейных уравнений:
A•p = b.
Таким образом, в сделанных предположениях обратная задача имеет единственное решение, если количество вертикальных граней модели шахтного поля четно, а количество индикаторных точек на дневной поверхности равно половине количества боковых граней.
Дополнительные замечания по организации и уточнению определения изменения естественного поля напряжений
С практической точки зрения для повышения точности решения обратной задачи, выбираемые индикаторные точки должны располагаться вокруг геометрического центра тяжести модели дневной поверхности шахтного поля на значительном расстоянии от центра.
Главная трудность в точном решении обратной задачи в данной формулировке – это определение горизонтальных смещений индикаторных точек дневной поверхности в абсолютной системе координат. Только в случае обеспечения достаточной точности таких измерений можно говорить об адекватном решении обратной задачи и определении изменения нагрузок на боковых вертикальных гранях модели шахтного поля.
Продемонстрированное решение обратной задачи определяет изменение среднего значения давления (или нормального напряжения) всей грани модели шахтного поля целиком относительно предыдущих положений горизонтальных координат датчиков на дневной поверхности, принятых за исходное состояние системы.
Для того чтобы получить более точную информацию о характере изменения давления по глубине при горизонтальном сдвиге датчиков положения, необходимо пробурить глубинные скважины по периметру предполагаемого шахтного поля и расположить датчики смещений не только на поверхности скважины, но и на глубинах, соответствующих серединам геологических слоев модели шахтного поля [10].
В этом случае решение обратной задачи будет также однозначным, и пользователь будет знать характер изменения давления по глубине, предполагая, что давление постоянно уже только на площади геологического слоя, а не всей торцевой поверхности модели шахтного поля.
Модуль решения обратной задачи с использованием параллелизуемых решений прямых задач
В связи с необходимостью автоматизации обработки геолого-механической информации о состоянии шахтного поля [11, 12] разработано программное обеспечение для автоматизации решения обратной задачи. В качестве инструментов для разработки ПО использовались платформа Java с библиотекой Swing и язык программирования Python.
Платформа Java использовалась, так как она позволяет создавать программное обеспечение, работающее на компьютерах с различными операционными системами и свободно переносимое между ними. Библиотека Swing также является мультиплатформенной и обеспечивает создание графического интерфейса.
Скрипт на языке Python используется для построения геометрии шахтного поля, и получения сетки конечных элементов на ее основе, включая группы для ограничений и приложения давлений. В нем для этих целей используются функции пакета Salome.
Главный интерфейс программы представляет собой окно с четырьмя закладками, в которых выполняются четыре основных этапа решения задачи:
1) построение сетки конечных элементов;
2) задание координат контрольных точек и получение номеров ближайших к ним узлов;
3) выполнение восьми расчетов с нагружением на разные грани модели шахтного поля и получение матрицы;
4) ввод фактических смещений на контрольных точках и получение результата.
Рис. 2. Поочередное приложение давления, принятого за единичное, на каждую в отдельности боковую поверхность модели шахтного поля для построения реперных решений
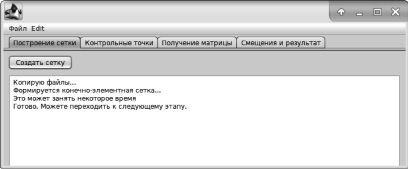
Рис. 3. Главный интерфейс программы для решения обратной задачи
Алгоритмическая последовательность действий при решении обратной задачи на разработанном программном обеспечении определяется последовательностью вкладок (рис. 3). При нажатии на первой вкладке выполняются служебные действия, при которых формируется модель шахтного поля, затем запускается Python скрипт, который с помощью пакета Salome формирует сначала полную геометрическую модель шахтного поля, а затем на ее основе конечно-элементную сетку.
Следующим этапом является ввод контрольных точек и нахождение ближайших к ним узлов конечно-элементной сетки. Для этого следует использовать вторую вкладку (рис. 3). В полях ввода вводятся координаты четырех точек, по нажатию кнопки Готово, открывается файл с сеткой и перебираются узлы в нем, с целью поиска узлов, наиболее близких к указанным координатам. Результат показывается в правом текстовом поле.
После выполнения данного этапа следует переходить к следующей вкладке: «Получение матрицы» (рис. 3). На этом этапе формируются файлы заданий для расчета каждого варианта прямой задачи.
Файлы заданий формируются программно, по два файла на каждый вариант. Первый файл описывает материалы модели, тип расчета, накладываемые на модель нагрузки и ограничения. Второй файл описывает параметры запуска, имена файлов и т.д.
Файлы заданий формируются на основе шаблонов, приведенных в приложениях. В ходе решения каждого варианта задачи процесс можно распараллеливать на необходимое количество потоков. Следует отметить, что программа будет сохранять работоспособность и при одном потоке.
Количество потоков ограничивается только количеством вычислительных ядер на вычислительной машине, где запускается данное ПО. Устанавливать количество потоков большее, чем имеется ядер в системе, нецелесообразно. Количество потоков можно ввести в окне интерфейса.
Также можно задать объем памяти, который следует выделить для решения задачи. Если необходимый объем не будет выделен, задача не сможет быть решена, даже если физически памяти в системе достаточно. Необходимый объем устанавливается экспериментально, например при 1 миллионе элементов минимально необходимый объем памяти составляет 16 ГБайт.
После построения матрицы следует ввести фактические перемещения на контрольных точках и получить значения давлений (вкладка «Смещение и результат»). Координаты смещений контрольных точек вводятся в левой части окна. Столбец с вычисленными значениями давлений на гранях модели выводится в текстовом поле в правой части окна. Кроме основного окна с вкладками интерфейс предусматривает окно настроек.
Очень важно не оставлять их пустыми а выбрать здесь, во-первых, рабочий каталог, в котором будут находиться все файлы моделей, расчетов и т.д., а во-вторых, каталог, в котором находится пакет Salome, так как с его помощью выполняются построения конечно-элементной сетки и решения прямых задач.
Заключение
Разработана общая методика решения обратной задачи для определения приращения давлений на боковых поверхностях модели шахтного поля по горизонтальным сдвижениям дневной поверхности шахтного поля. Она позволяет учесть в геомеханических расчетах изменение напряженного состояния на границах выработок любых полезных ископаемых в районах близких к сейсмически активным областям.
Разработан масштабируемый и параллелизуемый модуль решения обратных задач определения средних величин измененного природного поля напряжений по данным натурных измерений горизонтальных сдвижений дневной поверхности модели шахтного поля II и III горизонтов шахтного поля IV РУ ОАО «Беларуськалий».