В последнее десятилетие метод георадиолокации стали активно применять для решения самых разных инженерно-геологических, геотехнических задач. Метод георадиолокации основан на явлении отражения электромагнитной волны от границ неоднородностей в изучаемой среде, на которых скачкообразно изменяются электрические свойства – электропроводность и диэлектрическая проницаемость. При распространении георадарных сверхширокополосных импульсов в грунте на их амплитуду, фазовые характеристики и спектр частот влияют электрофизические свойства пород – электропроводимость, диэлектрическая и магнитная проницаемости в широком диапазоне частот. Они в свою очередь зависят от таких параметров грунта, как влажность и плотность горных пород, форма, размеры, взаимное расположение и ориентация минеральных зёрен или частиц и т.п.
Для совершенствования георадиолокационной аппаратуры, методик измерения и интерпретации их результатов актуальна разработка новых методов решения задач электродинамического моделирования, учитывающих изменение поляризации электромагнитной волны после отражения от границы неоднородности изучаемой среды. Наиболее широкое распространение для электродинамического моделирования получили такие методы, как FDTD, TLM и другие [1, 2]. Их основной недостаток – невозможность учета потерь в широком диапазоне частот, использование рекурсивных методов расчета и поэтому потребность в больших машинных ресурсах памяти и быстродействии.
С целью разработки более эффективного метода расчёта было предложено использовать дифференциальные ABCD-матрицы передачи [3], которые описывают малые участки оптической среды через матрицы передачи. Данный подход успешно реализован для расчета оптических систем в работе [4]. В работах [5–7] малые участки двухмерной слоистой среды с потерями были представлены в виде их матриц передачи. Это позволило записать ABCD-матрицы слоев, а их перемножение – матрица передачи всей среды и рассчитать электромагнитное поле на границе среды при облучении ее радиоимпульсом георадара.
В данной работе для учета поляризации электромагнитной волны (ЭМВ) предлагается уточненная модель среды, путем введения фиктивных диэлектрической и магнитной проницаемостей. Это позволяет в ABCD-матрице малых элементов среды учесть поляризацию ЭМВ. Для учета поляризационных и диссипативных потерь в широком диапазоне частот предлагается ввести два вида проводимостей – на низких и высоких частотах. Получен критерий устойчивости дифференциальных матриц, аналогичный критерию Куранта – Фредерикса – Леви.
Двухмерная электродинамическая модель среды
Под элементом пространства будем понимать часть среды, линейные размеры которой малы или стремятся к 0. Электродинамическое моделирование методом ABCD-матриц основано на представлении элементов среды матрицами передачи в виде отрезков электрических цепей с распределенными параметрами. Для этого вводятся комплексные проводимость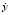 
и сопротивление 
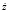среды:
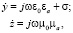(1)
где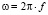 
– круговая частота; ε0, μ0, εа,μа – абсолютные и относительные диэлектрическая и магнитная проницаемости; σ – проводимость среды, позволяющая учесть тепловые и диссипативные потери.
В этом случае уравнения Максвелла запишутся [8]:
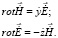(2)
Пусть плоскость YZ – граница, разделяющая среду 1 и среду 2, вектор Пойтинга П1 падающей ЭМВ лежит в плоскости XY, а вектор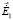 
ей перпендикулярен так, как это показано на рис. 1, а (случай горизонтальной поляризации). В среде 1 будут распространяться две волны: падающая П1 и отраженная П10. В среде 2 распространяется только прошедшая волна П2. Тогда 
, 
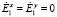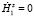и из (2) следует, что прошедшая ЭМВ будет описываться следующей системой уравнений:
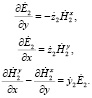(3)
Прошедшую ЭМВ П2 можно представить как две ортогональные связанные Т-волны П2x и П2y, где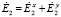 
(рис. 1, б).
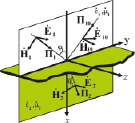
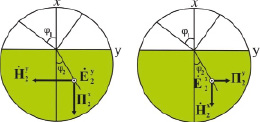
а) б)
Рис. 1. а) Падающая П1, отраженная П10 и прошедшая П2 электромагнитные волны; б) две ортогональных связанных Т-волны П2x и П2y, образующие прошедшую волну
Тогда третье уравнение в (3) можно разделить на два уравнения, если ввести фиктивные диэлектрические проницаемость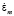 
и проводимость 
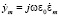, которые связывают 
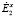и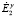 
и переписать (3) как
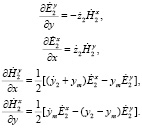(4)
Учет поляризационных и диссипативных потерь в среде
Внешнее электрическое поле вызывает в ионно-проводящих горных породах (песках, песчаниках, известняках и др.) различного вида поляризационные процессы. Для их учета необходимо знать время релаксации τрел, которое для большинства пород неизвестно. Но для многих пород известна зависимость проводимости σ и комплексной диэлектрической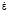 
от частоты [9–10]. Чтобы учесть в породах поляризационные и диссипативные потери введем два вида проводимостей – σст, σ∞ и два вида диэлектрических проницаемостей εст, ε∞ на низких и высоких частотах соответственно. Этому соответствует эквивалентная схема замещения рис. 2.
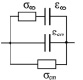
Рис. 2. Эквивалентная схема замещения диссипативных и поляризационных потерь, εст ,ε∞ , σст , σ∞ – диэлектрические проницаемости и проводимости среды на низких и высоких частотах соответственно
Тогда комплексную проводимость горной породы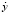 
в (2) можно записать как
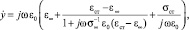(5)
где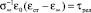 
– время релаксации.
Дифференциальная матрица передачи элемента среды
Рассмотрим случай вертикальной поляризации, когда вектор Е лежит в плоскости XY. Рассуждая аналогично вышесказанному, введя фиктивные магнитные проницаемость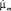 
и сопротивление 
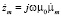, переходя аналогично (4) к конечным разностям: 
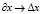и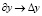 
записываем обобщенную дифференциальную матрицу передачи двухмерного элемента среды (ABCD-матрицу):
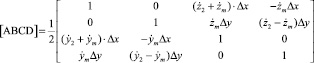, (6)
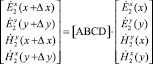. (7)
ABCD-матрице (6) можно поставить в соответствие эквивалентную схему элемента среды как восьмиполюсник (рис. 3).
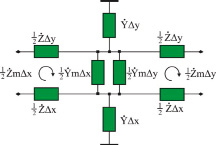
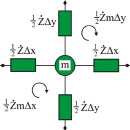
а) б)
Рис. 3. Эквивалентная схема элемента среды: а) в виде восьмиполюсника; б) упрощенный вариант а)
Расчет электрических полей
Дифференциальные ABCD-матрицы элементов среды позволяют записать ABCD-матрицы слоев, а их перемножение – матрицу передачи всего участка среды. Задавая соответствующие граничные условия, можно рассчитать распределение электрических полей в этой среде.
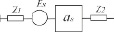
Модель элементов среды позволяет описать двухмерную среду, в общем случае состоящую из ячеек с разными электрофизическими свойствами. На рис. 4 показана такая модель, в которой двумерная среда представлена матрицей (M×N) элементов и состоящая из вектора внутренних сопротивлений источников (Z1), вектора источников ЭМВ (Es), каскадного соединения восьмиполюсников элементов среды (as, где as1, as2… asN – ABCD-матрицы слоев среды) и вектора волновых сопротивлений N + 1 среды (Z2).
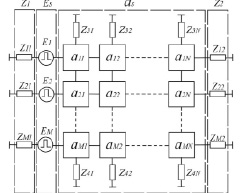
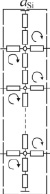
а) б) в)
Рис. 4. Эквивалентные схемы: а) двумерной неоднородной среды; б) результирующего многополюсника i-го слоя asi; в) результирующего многополюсника участка среды as
Объединяя элементы послойно, перемножая матрицы слоев, получаем результирующую ABCD-матрицу среды aS:
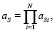(8)
в которой условия распространения Т-волн определяются граничными условиями среды слева и справа:
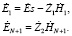(9)
Отсюда амплитуда магнитного поля справа:
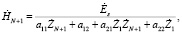(10)
где aij – элементы результирующей матрицы aS . Остальные амплитуды электрического и магнитного полей справа и слева находим из (9).
Устойчивость дифференциальных матриц передачи
Численное решение дифференциальных уравнений в частных производных сходится, при выполнении условия устойчивости
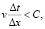(11)
где v – максимальная скорость переноса возмущения в среде, ?x – шаг по координате, Δt – шаг по времени, С – константа, которая в общем случае зависит от уравнения, но не зависит от Δx и Δt. Критерий назван в честь Рихарда Куранта, Курта Фридрикса и Ганса Леви (КФЛ). Физически критерий КФЛ означает, что возмущение за один шаг Δt по времени не должно продвинуться больше, чем на один пространственный шаг Δx.
Рассмотрим для простоты одномерную электродинамическую модель среды. Для нее дифференциальная матрица передачи элемента среды запишется как
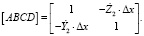(12)
Очевидно, что если модуль дискриминанта дифференциальной матрицы (12)
(13)
будет больше 1, то значения членов результирующей матрицы aS в результате умножения будут стремиться к бесконечности. Это будет значить, что решение потеряло устойчивость.
Введем параметр δ2, характеризующий отклонение det от 1 как
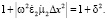(14)
Тогда можно записать условие сходимости процесса для заданного диапазона частот и δ при известном Δx:
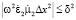, (15)
откуда условие устойчивости:
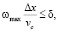(16)
где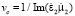 
– скорость распространения ЭМВ в среде, ωmax – максимальная круговая частота сигнала.
Например, если δ = 10-6, fmax = 109 Гц, vс = 3.108 м/с, то пространственный шаг не должен превышать Δx ≤ 0,477.10-7 м.
Заключение
В работе описан оригинальный метод электродинамического моделирования с помощью дифференциальных ABCD-матриц, которые описывают малые участки двухмерной слоистой среды. Введение фиктивных диэлектрической и магнитной проницаемостей позволило в ABCD-матрице малых элементов среды учесть поляризацию ЭМВ. Для учета поляризационных и диссипативных потерь в широком диапазоне частот введены два вида проводимостей – на низких и высоких частотах. Получен критерий устойчивости дифференциальных матриц, аналогичный критерию Куранта – Фредерикса – Леви. Записаны граничные условия на границах среды, которые позволяют рассчитать электромагнитное поле, как на границах, так и в самой среде при облучении ее радиоимпульсом георадара.
Работа выполнена в рамках программы фундаментальных исследований СО РАН (проект № 0382-2016-0001) и при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-45-140061 р_а).