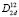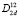Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

При моделировании новых, еще не синтезированных кристаллов необходимо удостовериться, что такие кристаллы представляют практический интерес, что они имеют реальные аналоги и, следовательно, могут быть не только получены экспериментально, но также окажутся достаточно прочными, устойчивыми и будут обладать интересными свойствами. Моделирование гипотетических Li-содержащих кристаллов LiMS2 со структурой халькопирита является важной задачей, поскольку они относятся к семейству известных и нашедших широкое применение материалов LiMX2 (M = B, Al, In, Ga; X = O, S, Se, Te) [1], многие из них пригодны для создания оптических приборов и устройств, работающих в среднем и дальнем ИК-диапазоне. О возможности существования у кристаллов LiMS2 структуры, подобной структуре халькопирита, свидетельствуют экспериментальные работы, в которых при разных внешних условиях были реализованы тетрагональные фазы халькопирита: при обычных условиях в LiInTe2 [2], LiAlTe2 [3] и LiGaTe2 [4]; при особых условиях, как в случае с LiInSe2 [5], и под высоким давлением при высокой температуре, как в синтезе фазы высокого давления у LiBO2 [6]. Особый интерес к таким Li-содержащим кристаллам [7], наиболее интенсивно разрабатываемым в последние несколько десятилетий, обусловлен не только наличием ряда уникальных свойств, среди которых можно выделить большую ширину запрещенной зоны (Eg > 2 эВ), высокий коэффициент теплопроводности и низкую анизотропию линейного теплового расширения, которые делают кристаллы LiMX2 более предпочтительными по сравнению с их кристаллохимическими аналогами, содержащими вместо атомов Li атомы Cu и Ag, но и развитие современных технологий, позволяющих использовать в производстве такие агрессивные материалы, как литий и его соединения. Весьма продуктивно и плодотворно в этом направлении работают в нашей стране исследователи под руководством Л.И. Исаенко [8]. Среди зарубежных публикаций, посвященных успешному выращиванию и изучению физических свойств Li-содержащих халькогенидов, в том числе сульфидов LiMS2, можно выделить работы [9, 10] Теоретическое исследование с использованием современных пакетов прикладных программ, основанных на первопринципном подходе, упругих и колебательных свойств кристаллов LiMS2 в тетрагональной фазе, подобной структуре халькопирита (CuFeS2), до сих пор не выполнено. Такие расчеты для гипотетических кристаллов LiMS2 являются актуальными, поскольку позволят получить необходимые сведения об устойчивости, прочности, свойствах, оптических частотах и, следовательно, о возможности существования и перспективах их синтеза.

Цель исследования: моделирование кристаллической структуры и исследование упругих и колебательных свойств кристаллов LiMS2 (M = B, Al, Ga, In) со структурой халькопирита с помощью методов теории функционала плотности и возможностей программного кода CRYSTAL14 [11].

Материалы и методы исследования

Для моделирования структуры халькопирита в избранных кристаллах LiMS2 (M = B, Al, Ga, In) необходимо определить параметры решетки a, c и координату аниона (атомы S) x. Тогда легко задать координаты восьми основных атомов в элементарной ячейке халькопирита: Li – (0,0,0) (0,½,¼); M – (0,0,½) (0,½,–¼); S – (x,¼,⅛) (–x,¼,⅛) (–¼,x,–⅛) (¼,–x,–⅛), в единицах a(1,1,γ),, в единицах a(1,1,?), где отношение ? = c/a характеризует тетрагональное сжатие, величина которого, как правило, изменяется в пределах от 1,5 до 2,0, а в отдельных кристаллах может даже превышать значение 2,0 (тетрагональное растяжение). Координата аниона x в кристаллах LiMS2 обычно отличается от идеального значения 0,25, что связано с окружением анионов катионами разного сорта. Для структуры халькопирита характерно тетрагональное расположение атомов относительно друг друга: катионы (Li, M) окружены четырьмя эквивалентными анионами S, а каждый анион S окружен парой атомов Li и парой атомов сорта M. Ближний порядок и химическая связь в структуре халькопирита обеспечиваются взаимодействием между атомами в катионных LiS4, MS4 и анионных Li2SM2 тетраэдрах.

Постоянные решетки a, c и координата анионов x вычислялись по формулам из работы [12], где за основу берутся радиусы соответствующих атомов. Полученные таким образом значения a, c и x использовались в качестве исходных, для проведения стандартной процедуры оптимизации геометрии кристалла, обеспечивающей приведение его в равновесное состояние с минимальной энергией. Равновесные значения a, c и x для кристаллов LiMS2 (M = B, Al, Ga, In), представлены в табл. 1.

Анализ равновесных параметров показывает, что кристаллическая ячейка должна быть сильно сжатой вдоль тетрагональной оси у трех кристаллов (LiBS2, LiAlS2, LiGaS2). Для них же в равновесном состоянии значения координаты x существенно отличаются от 0,25, что обусловлено различием длин связей Li-S и M-S. Максимальное отличие длин катион-анионных связей получено для LiBS2 (более 20 %), что характерно и для других соединений с большим тетрагональным сжатием (γ = c/a<<2), содержащих в своем составе атомы бора, например, LiBO2 [6] и CuBS2 [13]. Катионные LiS4, InS4 и анионные Li2SIn2 тетраэдры в кристалле LiInS2 должны быть слабо искажены, поскольку длины связей Li-S и In-S практически совпадают.

Модельные расчеты для кристаллов LiMS2 (M = B, Al, Ga, In) были выполнены с помощью методов теории функционала плотности DFT (density functional theory), которые составляют основу программного кода CRYSTAL [11]. Для обеспечения надежности результатов расчетов, кроме оптимизации геометрии кристаллов, был применен гибридный метод B3LYP и разбиение зоны Бриллюэна сеткой из специальных точек 16×16×16, что обеспечивало сходимость по полной энергии не хуже 10-3 эВ/атом и по фононным частотам в пределах нескольких десятых долей см-1. Все расчеты проводились с использованием полноэлектронного валентно-расщепленного базиса гауссовых орбиталей TZVP (Triple-Zeta Valence), реализуемого в программном коде CRYSTAL14 [11].

Результаты исследования и их обсуждение

Механические свойства моделируемых кристаллов LiMS2 (M = B, Al, Ga, In), вычисленные из первых принципов, позволяют оценить их устойчивость и прочность. С помощью кода CRYSTAL были получены упругие постоянные, представленные в табл. 2. Там же приведены фундаментальные физические характеристики: модуль Юнга E, модуль сдвига G, модуль всестороннего сжатия K и коэффициент Пуассона ν.

Все моделируемые кристаллы LiMS2 являются устойчивыми, поскольку вычисленные упругие постоянные удовлетворяют условиям Борна для тетрагональных кристаллов: диагональные компоненты Cii > 0 (i = 1, 3, 4, 6), а между остальными компонентами выполняются соотношения C11 > C12, C11C33 > C132 и (C11 + C12)C33 > 2C132. Поскольку в кристаллах LiMS2 отношения K/G ≥ 1,75 и G/K ≤ 0,8, то их можно отнести к прочным и пластичным материалам, у которых ионность связи Li-S много выше ионности преимущественно ковалентных связей M-S.

Вычисленные в модели Зенера показатели анизотропии A = 2C44/(C11-C12) превышают 1, что свидетельствует о сильно выраженной анизотропии структуры и свойств моделируемых кристаллов LiMS2 (M = B, Al, Ga, In).

Таблица 2

Упругие постоянные (Cij), модули упругости (E, G, K), микротвёрдость (H) и параметр Грюнайзена (γG) (в ГПа), коэффициент Пуассона (ν) и показатель анизотропии (A) кристаллов LiMS2 со структурой халькопирита

Прочность и устойчивость материала напрямую связаны с его сопротивляемостью внешним механическим нагрузкам, которые характеризуются микротвердостью, определяемой из эксперимента, как правило путем вдавливания в образец алмазных пирамид. Микротвердость кристаллов LiMS2 была вычислена с помощью коэффициента Пуассона (ν) и модуля Юнга (E) по формуле H = E(1 – 2ν)/6(1 + ν), взятой из работы [14]. Судя по величине H, в четыре и более раз превышающей микротвердость золота (0,66 ГПа), но много меньшей порогового значения для сверхтвердых материалов (40 ГПа), кристаллы LiMS2 являются достаточно прочными и устойчивыми, что не противоречит выводам, полученным ранее из соотношений модулей сдвига и всестороннего сжатия (K/G ≥ 1,75 и G/K ≤ 0,8).

Параметр Грюнайзена (γG) является мерой ангармонизма межатомных взаимодействий в кристаллах, не может превышать величину 4,5 и может иметь среднее значение в пределах от 0,85 до 3,53. Вычисленные по формуле γG = 3(1 + ν)/2(2 – 3ν) из работы [15] значения параметров Грюнайзена для моделируемых кристаллов LiMS2 не противоречат данным требованиям.

В рамках теории функционала плотности был выполнен расчет частот оптических фононов в точке Г зоны Бриллюэна тетрагональных кристаллов LiMS2, значения которых и вкладов колебаний атомов представлены в табл. 3.

Полное преобразование длинноволновых нормальных колебаний (Гtotal) по неприводимым представлениям в центре зоны Бриллюэна халькопирита (точка Г) содержит вклады одного двукратного Г5 (E) и четырех однократных Г1 (A1), Г2 (A2), Г3 (B1), Г4 (B2) неприводимых представлений. Это преобразование разлагается в ряд: Гtotal = A1 + 2A2 + 3B1 + 4B2 + 7E, в котором присутствуют три акустические моды (B2 и E). Исключая акустические моды, получаем разложение для оптических частот: Гopt = A1 + 2A2 + 3B1 + 3B2 + 6E. Теоретико-групповой анализ и оценка процентного вклада отдельных атомов в колебания определенной симметрии, позволяют получить полную картину колебаний в равновесном кристалле.

Установлено, что колебания Г1 (A1) и Г2 (A2) на 100 % являются анионными, все смещения происходят в направлении главной оптической (тетрагональной) оси кристалла (ось z) и перпендикулярно к ней. Частоты колебаний убывают в гомологическом ряду LiBS2>LiAlS2>LiGaS2>LiInS2.

В колебательной моде Г3 (B1) атомы Li и M (B, Al, Ga, In) смещаются только вдоль тетрагональной оси (ось z), при этом катионы (атомы Li или M) колеблются в противофазе, а анионы (атомы S) смещаются в плоскостях, перпендикулярных оси z. Колебания создают катион-анионные пары (Li-S и M-S), изменения вкладов в которые свидетельствуют об ослаблении химической связи в изоэлектронном ряду LiBS2>LiAlS2>LiGaS2>LiInS2.

В колебательной моде с симметрией Г4 (B2) катионы Li и M (B, Al, Ga, In) смещаются только вдоль тетрагональной оси (ось z), анионы (атомы S) совершают колебания исключительно в плоскостях, содержащих ось z. Колебания создаются катион-анионными парами (Li-S и M-S), а наблюдаемые изменения вкладов в них свидетельствует об ослаблении ковалентной составляющей химической связи в ряду LiBS2>LiAlS2>LiGaS2>LiInS2.

В колебательной моде с симметрией Г5 (E) атомы Li и M (B, Al, Ga, In) смещаются только в плоскостях, перпендикулярных тетрагональной оси (ось z), в анионы (атомы S) колеблются в плоскостях, содержащих эту ось. Две верхние моды во всех соединениях LiMS2 содержат преобладающий вклад колебаний легкого катиона (атомы Li) с небольшой долей анионов (атомы S). Для самой низкой частоты вклады от катионной подрешетки Li не превышают 8 %, а доля вклада катиона M увеличивается с увеличением атомного номера в ряду B>Al>Ga>In, на фоне уменьшения доли вкладов аниона S.

В комбинационном рассеянии (КР) кристаллов LiMS2 со структурой халькопирита активны все моды, кроме A2. Инфракрасные (ИК) спектры поглощения этих кристаллов содержат полярные моды B2 и E, расщепленные на продольные (LO) и поперечные (TO) составляющие. Основными причинами расщепления являются взаимодействие катионов с анионами и различие масс атомов, заполняющих кристаллические подрешетки: m(Li) = 7,0160, m(B) = 11,0093, m(Al) = 26,9815, m(Ga) = 68,9257, m(In) = = 114,9041, m(S) = 31,9721 (в а.е.м.). В данном случае влияние массы атомов проявляется в амплитудах колебаний отдельных атомов в соответствующих подрешетках (Li, M, S), а также в колебаниях катион-анионных пар (Li-S и M-S), отражающих прочность взаимодействия в катионных тетраэдрах LiS4 и MS4.

Упругие волны, распространяющиеся в тетрагональных кристаллах со структурой халькопирита, разделяются на три фазовые скорости, из которых две – квазипоперечные (υT1, υT2) и одна – квазипродольная (υL). Вычисленные для кристаллов LiMS2 значения фазовых скоростей представлены в табл. 4. Из таблицы видно, что значения всех фазовых скоростей уменьшаются в ряду LiBS2>LiAlS2>LiGaS2>LiInS2 и имеют максимальное значение в направлениях [101] и [011].

Заключение

Полученные равновесные параметры кристаллической структуры и спектры частот оптических колебаний позволяют идентифицировать новые кристаллы LiBS2, LiAlS2, LiGaS2 и LiInS2 в тетрагональной фазе халькопирита с пространственной группой симметрии 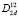(или I-42d, № 122). Эти данные для гипотетических соединений LiMS2 могут служить ориентиром и быть полезными экспериментаторам при попытке синтезировать модельные образцы, а также при исследовании возможностей фазовых переходов в уже синтезированных кристаллах LiMS2 в орторомбической модификации. Вычисленные упругие постоянные всех моделируемых соединений полностью удовлетворяют условиям Борна, что может свидетельствовать об устойчивости тетрагональных фаз кристаллов LiMS2 при условии их успешной реализации. Получены данные об изменении упругих и колебательных свойств при изменении химического состава, что представляет научный и практический интерес, при поиске новых прочных и широкозонных (Eg > 2 эВ) материалов LiMS2 (M = B, Al, Ga, In) с полупроводниковыми свойствами.