Проектирование разработки нефтегазовых месторождений в районах распространения многолетней мерзлоты обязательно должно включать в себя оценку теплового воздействия эксплуатационных скважин на окружающие мерзлые породы, поскольку во время добычи углеводородов пластовые флюиды, поднимаясь по скважине из больших глубин с высокими температурами, нарушают тепловое равновесие вышележащих мерзлых пород. При этом окрестность добывающих скважин оттаивает, появляется риск дестабилизации околоскважинной зоны и крепления скважин. От размеров ореола оттаивания и динамики его развития зависят возможные негативные последствия этого процесса. Прежде всего, это потеря устойчивости верхней части ствола скважин, вследствие чего создаются предпосылки для потери герметичности обсадных колонн. Также это просадки верхнего слоя пород в окрестности устья скважин, что приводит к повреждению устьевого оборудования и опасным деформациям промысловых сетей [1–3].
В свою очередь, из-за теплового взаимодействия с горными породами и адиабатического расширения (сжатия) добываемого флюида происходит изменение его температуры. Эти процессы взаимосвязаны, поэтому задача определения температуры горных пород может быть решена только в сопряженной постановке, т.е. при одновременном вычислении как температуры флюида в скважине, так и температурного поля окружающих горных пород.
В работах [3–5] подобная задача решалась для одиночных газовых скважин в осесимметричной постановке. Актуальность данного подхода ограничена, поскольку множество современных нефтяных и газовых месторождений разрабатываются кустовым бурением, где скважины расположены на небольшом расстоянии между собой в радиусе теплового влияния. Таким образом, возникает необходимость в решении задачи теплового взаимодействия куста скважин с горными породами в двухмерной или трехмерной постановке. Причем из-за сложности геометрии подобную задачу целесообразно решать с помощью численного моделирования с использованием метода конечных элементов [6–8].
В работе [9] была поставлена задача определения времени смыкания ореолов протаивания между соседними скважинами в одном кусте. Вместо численных методов было предложено использовать расчетный метод соотношения тепловых потоков. В результате выведена зависимость времени фазового перехода при оттаивании многолетнемерзлой породы вокруг скважины от радиуса оттаивания без учета затрат тепла на нагрев талой и мерзлой зон.
В работе [10] приведены результаты численного решения задачи Стефана в трехмерной постановке, описывающей динамику протаивания грунтов в зоне влияния двух добывающих скважин. Двухфазная задача Стефана сформулирована в виде нестационарного уравнения теплопроводности с начальными и граничными условиями. Выделение или поглощение тепла при фазовом превращении учитывается путем ввода в нестационарное уравнение теплопроводности сосредоточенной теплоемкости на границе фазового перехода. Однако авторы в своей работе пренебрегают охлаждением добываемого газа при подъеме от забоя к устью вследствие тепловых потерь и дросселирования.
Целью настоящей работы является оценка величины ореола оттаивания многолетнемерзлых пород в окрестности куста из трех вертикальных газодобывающих скважин для условий месторождений Лено-Вилюйской нефтегазоносной провинции в двухмерной постановке.
Математическая модель исследуемого процесса включает в себя: уравнение теплопроводности, описывающее распространение тепла в горных породах с учетом их возможного оттаивания – промерзания; уравнение теплопереноса, описывающее изменение температуры добываемого газа; необходимые граничные и начальные условия, определяемые характером сопряжения тепловых потоков на стенке скважин. При построении математической модели используются некоторые допущения. Во-первых, полагаем, что тепловой поток в каждом сечении скважины распространяется строго радиально по горизонтальной плоскости, перпендикулярной оси скважин, а распространение тепла по вертикали пренебрежимо мало в силу симметрии задачи. Во-вторых, при расчете температурного поля горных пород пренебрегаем массообменными процессами.
В области горных пород от забоя скважины до подошвы многолетней мерзлоты теплофизические коэффициенты в уравнении теплопроводности являются кусочно-постоянными (они определяются типом горных пород, слагающих геологический разрез), и решение соответствующей задачи теплопроводности может быть выполнено стандартными методами. В области многолетней мерзлоты эта задача осложняется, так как здесь необходимо учитывать фазовый переход «лед – вода», и для численного решения задачи Стефана [11] используется метод сквозного счета со сглаживанием разрывных коэффициентов в уравнении теплопроводности по температуре в окрестности фазового перехода (метод Самарского – Моисеенко без явного выделения фронта фазового перехода) [12]. Приведем уравнение теплопроводности:
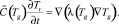(1)
Здесь Tg – температура горных пород;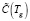 
– кусочно-постоянная объемная теплоемкость горных пород со скрытой теплотой фазового перехода, зависящая от температуры Tg; λ(Tg) – кусочно-постоянный коэффициент теплопроводности горных пород, также зависящий от температуры Tg.
При решении задачи в сопряженной постановке следует учитывать резкое различие характерного времени переходных процессов в скважинах, где происходит перенос тепла за счет вынужденной конвекции и скорости потока имеют порядок 1 м/с, и в горных породах, где скорость кондуктивного переноса тепла очень мала из-за малости коэффициента температуропроводности. Это различие еще больше усугубляется при фазовых переходах влаги в мерзлых горных породах, так как скорость движения границы раздела фаз много меньше скорости распространения температурного возмущения. Очевидно, что по этим причинам перенос тепла в скважинах можно моделировать стационарными уравнениями, в которое время будет входить параметрически через медленно изменяющуюся температуру горных пород в слагаемом, описывающем теплообмен движущегося газа с горными породами. В таком случае, уравнения теплопереноса запишутся в виде [4, 13, 14]:
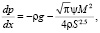(2)
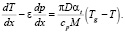(3)
Здесь x – вертикальная координата вдоль оси скважины; p – давление газа; ρ – плотность газа; g – ускорение свободного падения; ψ – коэффициент гидравлического сопротивления; M – постоянный массовый расход; S – поперечное сечение скважины; T – температура газа; ε – коэффициент дросселирования; D – диаметр проходного сечения; αt – суммарный коэффициент теплопередачи через стенку скважины; cp – удельная теплоемкость газа при постоянном давлении.
Эти два уравнения дополняются уравнением состояния реального газа, в котором кофициент несовершенства вычисляется по формуле Латонова – Гуревича [4].
Связь для перехода от одного сечения в области горных пород к другому осуществляется через решение уравнений трубной гидравлики относительно давления и температуры газа [4, 13, 14], и граничное условие на наружной стенке скважины, где в суммарном коэффициенте теплопередачи учитываются термические сопротивления слоев конструкции скважины (насосно-компрессорных труб, кольцевого затрубного пространства, обсадной колонны, возможной теплоизоляции и т.д.).
Вычислительный эксперимент
Расчетная область в массиве горных пород представляет собой параллелепипед со сторонами 40 м в длину, 10 м в ширину и в глубину от поверхности до забоя скважин. На одной из больших граней расположены три вертикальные скважины с диаметрами 0,14 м на расстоянии 10 м друг от друга. Моделирование распространения тепла проводится отдельно на разных глубинах в двухмерных областях 40×10 м (рис. 1), так как предполагаем, что тепловой поток в каждом сечении скважины распространяется строго радиально по горизонтальной плоскости. Температуры околоскважинных зон на разных глубинах будут отличаться, поскольку в зависимости от глубины меняются температура газа в скважинах, начальная температура и теплофизические свойства окружающих пород.
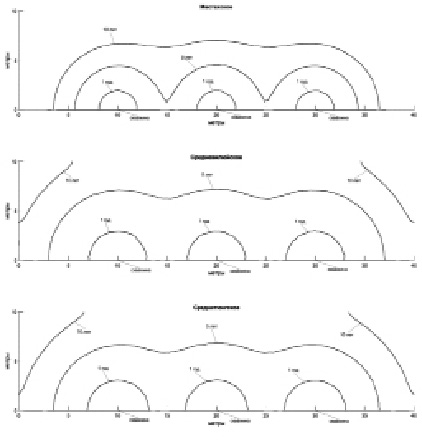
Рис. 1. Границы оттаивания вокруг куста из трех скважин на глубине 100 м через 1 год, 5 лет и 10 лет эксплуатации в горизонтальном разрезе
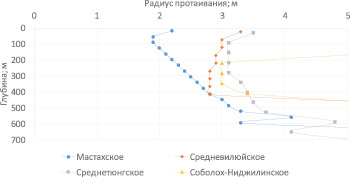
Рис. 2. Зависимость радиуса оттаивания многолетнемерзлых пород вокруг газодобывающей скважины от глубины на месторождениях после 1-го года эксплуатации
На гранях, удаленных от скважин, ставится граничное условие II рода, согласно которому тепловой поток, проходящий через грани, равен нулю. Начальное распределение температуры горных пород в момент пуска скважин задается в виде функции, зависящей только от вертикальной координаты, по данным термокаротажа. Поставленная задача теплопроводности решается методом конечных элементов. Характерный размер треугольной ячейки в сетке разбиения составляет порядка 0,5 м.
Температура и давление газа в скважинах вычисляются из решения задачи Коши первого порядка – уравнения (2)–(3) дополняются начальными условиями на забое в виде пластовых температуры и давления. Эти параметры газа определяются на каждом временном шаге после расчета поля температур в окружающих скважины породах. В свою очередь, температурное поле в породах рассчитывается в зависимости от температуры газа, найденной на предыдущем шаге по времени. Суммарный коэффициент теплового взаимодействия газа и породы через стенку скважины принят равным 6,871 Вт/(м2∙ °С), что соответствует отсутствию теплоизоляции.
Основные исходные данные численного расчета приведены в таблице. Температурное поле массива горных пород в окрестности куста скважин прогнозируется на 10 лет эксплуатации.
Основные исходные данные вычислительного эксперимента
|
Параметр |
Значение |
|||
|
Месторождение |
Мастахское |
Средневилюйское |
Среднетюнгское |
Соболох-Ниджилинское |
|
Глубина пласта; м |
1800 |
2450 |
3100 |
3150 |
|
Подошва многолетнемерзлых пород; м |
610 |
450 |
670 |
400 |
|
Геотермический градиент в мерзлой зоне; °С/1000 м |
3,5 |
–0,8 |
4,1 |
–3,5 |
|
Геотермический градиент в талой зоне; °С/1000 м |
43,2 |
32,7 |
36,9 |
32,8 |
|
Пластовая температура; °С |
40 |
55 |
73 |
76 |
|
Пластовое давление; атм |
110 |
160 |
320 |
380 |
|
Массовый дебит; кг/с |
2 |
6 |
4.8 |
4 |
Результаты исследования и их обсуждение
На рис. 1 представлены границы оттаивания вокруг куста из трех скважин в верхнем слое пород без учета погодно-климатических условий на дневной поверхности для Мастахского, Среднетюнгского и Средневилюйского месторождений.
Из рис. 1 следует, что многолетнемерзлые породы в окрестности газодобывающих скважин монотонно протаивают все время их эксплуатации, и к 5-ому году непрерывной добычи с заданным средним дебитом ореолы оттаивания соседних скважин сливаются. Относительно меньшие радиусы оттаивания на Мастахском месторождении обусловлены меньшими дебитом, пластовыми температурой и давлением.
Согласно работе [5] данный процесс можно разделить на 3 стадии. Во время первой, начальной, стадии оттаивание вокруг скважин идет как бы изолированно и скважины практически не влияют друг на друга. На второй стадии талики вокруг скважин сливаются. Третья стадия характеризуется замедлением движения границы оттаивания и переходом в квазистационарный режим. В нашем случае картине оттаивания после 1-го года эксплуатации соответствует I-я стадия, состоянию после пяти лет эксплуатации – II-я стадия, а состоянию после десяти лет эксплуатации – II-я или III-я стадия.
На рис. 2 построены зависимости радиусов оттаивания мерзлых горных пород от глубины. Видно, что на Мастахском и Среднетюнгском месторождениях ореол оттаивания мерзлых пород постепенно растет с глубиной. Это может быть обусловлено положительным геотермическим градиентом в области мерзлых пород (таблица). Напротив, на Средневилюйском месторождении, где наблюдается отрицательный геотермический градиент в области мерзлых пород, радиус оттаивания обратно пропорционально зависит от глубины. На Соболох-Ниджилинском месторождении верхние слои горных пород (до 150 м) изначально находятся в талом состоянии, поэтому радиусы оттаивания определены только для небольшого интервала 150–400 м.
Из результатов вычислительного эксперимента можно сделать вывод, что в условиях Лено-Вилюйской нефтегазоносной провинции нетеплоизолированные газодобывающие скважины существенно нарушают тепловой режим окружающих их многолетнемерзлых пород. В случае кустового расположения талики вокруг скважин соединяются уже в начальный период эксплуатации. Из этого следует, что решение тепловой задачи для одиночной скважины не способно вполне описать реальную картину оттаивания горных пород вокруг куста скважин. Необходимо двухмерное моделирование, а рядом с дневной поверхностью, в зоне влияния атмосферных условий – трехмерное.
Заключение
Проведен численный расчет задачи теплового взаимодействия куста газовых скважин с окружающими многолетнемерзлыми породами для условий эксплуатации четырех месторождений Лено-Вилюйской нефтегазоносной провинции.
Построено количественное описание теплового режима куста скважин и окружающих пород в период до 10 лет непрерывной эксплуатации с заданным средним дебитом. Выявлено, что ореолы оттаивания мерзлых пород вокруг соседних скважин монотонно расширяются и в итоге сливаются в один. Причем ореолы оттаивания возрастают с глубиной на Мастахском и Среднетюнгском месторождениях и уменьшаются при увеличении глубины на Средневилюйском.