Как известно [1], измерения угловых и частотных флуктуаций декаметрового радиосигнала, отраженного от ионосферы, можно использовать для исследования тонкой структуры околоземной плазмы. Между тем для успешной постановки экспериментов по изучению ионосферных неоднородностей целесообразно предварительно рассчитать ожидаемые величины этих флуктуаций на разных рабочих частотах на системе трасс. Сделать строгие аналитические расчеты флуктуаций характеристик сигнала при наклонном зондировании случайно-неоднородной ионосферы не представляется возможным. В этом случае для решения задачи можно применить имитационное моделирование, основанное на методе Монте-Карло [2]. Однако при использовании метода статистических испытаний на трассах наклонного зондирования существует большая проблема, связанная с тем, что для каждой реализации случайной функции диэлектрической проницаемости ионосферы необходимо решать краевую задачу электродинамики. Последнее требует больших вычислительных ресурсов для проведения расчетов. Более того, метод Монте-Карло не позволяет установить функциональные связи между флуктуациями характеристик сигнала и параметрами ионосферных неоднородностей.
Альтернативным вариантом расчета статистических характеристик сигнала являются приближенные аналитические методы теории случайных полей [3], использующие физические представления о корреляционных свойствах тонкой структуры ионосферы. Результатом применения приближенных методов обычно являются сложные интегральные выражения для статистических моментов флуктуационных характеристик сигнала. Использование этих выражений для моделирования и интерпретации реальных данных измерений ионозонда требует разработки специальных численных алгоритмов.
Цель работы заключается в развитии аппарата численно-аналитического моделирования угловых и частотных флуктуаций декаметрового радиосигнала для интерпретации данных измерений на трассах наклонного зондирования ионосферы.
Основные теоретические соотношения
Для расчета угловых и частотных флуктуаций радиосигнала в ионосфере используем стохастические дифференциальные уравнения лучевого приближения [3]:
, 
,
,
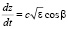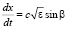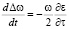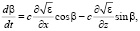(1)
где z, x, β – характеристики луча; Δω – доплеровский сдвиг частоты, ε – случайная функция диэлектрической проницаемости ионосферы, dt – элемент группового времени запаздывания. Решения уравнений (1) получим с помощью метода малых возмущений [3] с учетом фиксированного положения пунктов излучения и приема ионозонда. Введем представление:
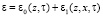, (2)
где ε0 – средняя составляющая, ε1 – малая случайная компонента, характеризующая ионосферные неоднородности (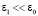
, 
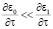), τ – время. Решения уравнений (1) будем искать в виде
, 
, 
,
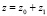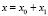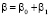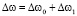, (3)
где z0, x0, β0, Δω0 – соответственно текущие координаты траектории сигнала, угол рефракции и доплеровский сдвиг частоты в средней ионосфере; z1, x1, β1, Δω1 – флуктуации характеристик сигнала, вызванные случайными неоднородностями.
Подставляя (2), (3) в уравнения (1) и проводя асимптотические разложения, имеем
, 
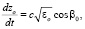
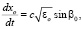
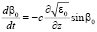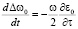, (4)
, 
,
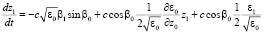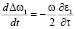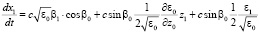, (5)
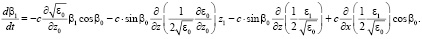
Получить аналитические решения детерминированных нелинейных уравнений (4) с заданными краевыми условиями в случае произвольной функции ε0(z) не представляется возможным, однако эти уравнения можно решить методами численного интегрирования [2]. Между тем для определения флуктуаций угла прихода и доплеровского смещения частоты радиосигнала в приемном пункте ионозонда можно решить линейную неоднородную систему стохастических дифференциальных уравнений (5) с краевыми условиями,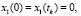 
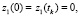
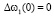. Применяя для решения системы (5) метод Лагранжа [4], в случае пологих траекторий сигнала в средней ионосфере, получаем
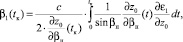(6)
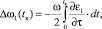(7)
где βн = β(0) – угол выхода луча в пункте излучения ионозонда. Составляя на основе (6), (7) выражения для статистических моментов и проводя усреднение по ансамблю неоднородностей, для дисперсии вертикального угла прихода и доплеровского сдвига частоты радиосигнала в приемном пункте ионозонда имеем
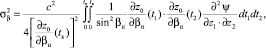(8)
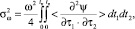(9)
где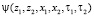 
– корреляционная функция случайного поля неоднородностей ионосферы. Полагая, что поле неоднородностей обладает свойствами квазистационарности и квазиоднородности, а движение неоднородностей можно учесть в рамках гипотезы о переносе замороженной турбулентности [3], функцию корреляции зададим в виде
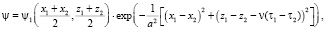(10)
где a – пространственный радиус корреляции флуктуаций диэлектрической проницаемости, равный внешнему масштабу турбулентности ионосферы [5]. Считая, что внешний масштаб турбулентности ионосферы a мал по сравнению с масштабом изменения функции ψ1 и толщиной ионосферы, интегралы (8), (9) можно вычислить асимптотически:
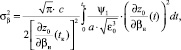(11)
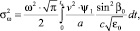(12)
где интегрирование проводится по суммарной переменной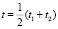 
. Для интерпретации данных измерений ионозонда представляет интерес статистическая связь флуктуаций сигнала во времени и в пространстве. Составляя на основе выражений (6), (7) смешанный статистический момент для функции взаимной корреляции и проводя вычисления при тех же предположениях, что и при выводе (11), (12), получаем
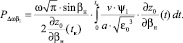(13)
Считая в интегралах (11)–(13) верхний предел переменным и дифференцируя их по верхнему пределу, получим обыкновенные дифференциальные уравнения для определения статистических моментов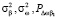 
. Записывая полученные уравнения совместно с уравнениями (4) и добавляя к ним дифференциальные уравнения для определения функций z0, β0, продифференцированных по начальному параметру βн, получим полную систему уравнений для одновременного расчёта средних и флуктуационных характеристик вертикального угла прихода и доплеровского сдвига частоты радиосигнала на трассе наклонного зондирования ионосферы. Эта система имеет следующий вид:
,
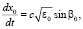
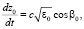
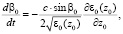
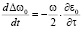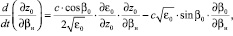(14)
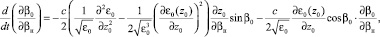
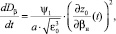
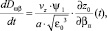
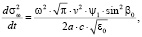
где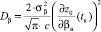 
, 
.
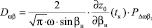Математическое моделирование и обсуждение результатов расчетов
Для демонстрации работы предложенного аппарата численно-аналитического моделирования на рис. 1, 2 в качестве примера приведены результаты расчетов на основе системы (14) угловых и частотных флуктуаций радиосигнала на трассах различной протяженности. При моделировании среднеквадратичного отклонения флуктуаций угла прихода в пункте приема ионозонда σβ(xк) средняя диэлектрическая проницаемость ионосферы представлялась двухслойной моделью:
(15)
где χ – параметр включения нижней ионизации, zme, yme, fкре – высота минимума диэлектрической проницаемости (максимума электронной концентрации), полутолщина и критическая частота слоя E соответственно; zm, ym, fкр – высота максимума, полутолщина и критическая частота слоя F2. Неоднородная часть корреляционной функции задавалась в виде: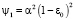 
, где α2 – интенсивность неоднородностей электронной концентрации. На рис. 1 представлены значения σβ на трассах различной протяженности для нескольких рабочих частот зондирования. При моделировании задавались следующие типичные параметры ионосферного слоя F2: zm = 300 км, ym = 100 км, fкр = 6 МГц. Нижележащий слой E был представлен параметрами: zme = 125 км, yme = 25 км, fкре = 3 МГц. При расчетах параметры неоднородностей составляли: a = 10 км, α2 = 0,008. Из рис. 1 следует, что в однослойной ионосфере (χ = 0) при заданной рабочей частоте в окрестности некоторого угла выхода радиосигнала βн происходит увеличение угловых флуктуаций σβ в пункте приема ионозонда. Это связано с тем, что данная рабочая частота приближается к окрестности максимально-применимой частоты (МПЧ) радиотрассы, длина которой определяется углом выхода βн. В случае полного совпадения рабочей частоты и МПЧ радиотрассы для выбранного угла выхода βн, величина σβ сильно возрастает, что связано с уменьшением в этих условиях знаменателя у коэффициента перед интегралом в формуле (11).
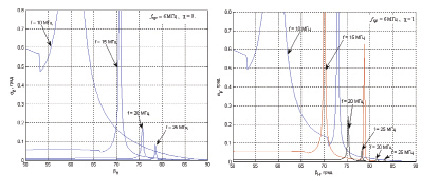
Рис. 1. Среднеквадратичное отклонение вертикального угла прихода на трассах наклонного зондирования однослойной (χ = 0) и двухслойной (χ = 1) ионосферы для различных рабочих частот, α2 = 0,008, a = 10 км
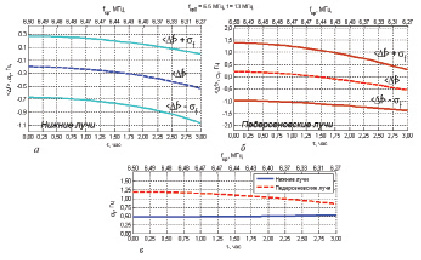
Рис. 2. Частотные флуктуации декаметрового радиосигнала (f = 13 МГц) на односкачковой радиотрассе протяженностью X = 1500 км, при χ = 0, v = 0,1 км/c, a = 10 км, α2 = 0,0004
Угловые флуктуации радиосигнала отличаются на трассах различной протяженности и существенно зависят от рабочей частоты. С увеличением рабочей частоты максимальные значения σβ возникают на более высоких частотах, что связано с увеличением длины трассы, соответствующей МПЧ. При распространении сигнала на разных рабочих частотах в двухслойной ионосфере (χ = 1), в зависимостях σβ от угла выхода возникают дополнительные максимумы. Их появление связано с отражением радиосигнала от нижнего слоя ионосферы
Расчеты частотных флуктуаций декаметрового радиосигнала на трассе наклонного зондирования нестационарной случайно-неоднородной ионосферы были выполнены для модели (15), в которой отсутствовал нижний слой E (χ = 0), а критическая частота слоя F2 изменялась от времени по закону: fкр(τ) = fкр0 – bτ2, где fкр0 – критическая частота в начальный момент времени τ = 0, b – размерный параметр. На рис. 2 представлены результаты расчета среднеквадратичного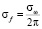 
и среднего 
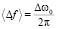доплеровского смещения частоты радиосигнала на трассе протяженностью X = 1500 км. При этом рабочая частота составляла f = 13 МГц, скорость вертикального движения поля неоднородностей – v = 0,1 км/c, масштаб неоднородностей a = 10 км. Численные значения параметров средней ионосферы составляли: zm = 300 км, hm = 100 км, fкр0 = 6,5 МГц. Из рис. 2 следует, что на фиксированной односкачковой трассе вследствие временных вариаций критической частоты ионосферы происходят изменения длины нижних и верхних траекторий радиосигнала. Последнее оказывает существенное воздействие на значения частотных флуктуаций и среднего доплеровского сдвига рабочей частоты. Так уменьшение со временем критической частоты слоя F2 влечет за собой существенно разное поведение верхней и нижней траекторий, а именно, длина верхней траектории сокращается, а длина нижней растет. Вследствие этого эффекта в пункте приема ионозонда с течением времени будет фиксироваться рост частотных флуктуаций нижней моды. Между тем для Педерсеновской моды частотные флуктуации будут уменьшаться со временем. Важно заметить, что в нестационарной ионосфере средние значения доплеровского сдвига частоты нижней и Педерсеновской мод могут оказаться не только существенно разными по количественным значениям, но противоположными по знаку.
Заключение
Для интерпретации данных измерений угловых и частотных флуктуаций декаметровых радиосигналов на трассах наклонного зондирования ионосферы развит аппарат математического моделирования статистических моментов этих флуктуаций с использованием аналитических и численных методов. В качестве модели тонкой структуры околоземной плазмы использована эффективная модель пространственно-временной корреляционной функции, характеризующей квазиоднородное по пространству и по времени случайное поле неоднородностей. Движение случайных неоднородностей учтено в рамках гипотезы о переносе замороженной турбулентности. В качестве модели высотного профиля электронной концентрации ионосферы может быть произвольная аналитическая функция. На основе приближения геометрической оптики и метода малых возмущений получена система обыкновенных дифференциальных уравнений первого порядка для одновременного численного расчета средних значений, дисперсий и функции взаимной корреляции вертикального угла прихода и доплеровского сдвига частоты декаметрового радиосигнала в широком диапазоне рабочих частот на трассе наклонного зондирования. Проведенное численно-аналитическое моделирование на основе полученной системы уравнений для типичных ионосферных условий показало хорошую работоспособность предложенного математического аппарата, и его можно использовать для расчетов статистических моментов угловых и частотных флуктуаций декаметрового радиосигнала на трассах различной протяженности.