Важным инструментом при внедрении современных наукоемких технологий в практику растениеводства являются динамические модели продукционного процесса сельскохозяйственных растений, роль которых возрастает в свете нового перспективного тренда развития сельскохозяйственной отрасли – устойчивого и точного земледелия [1]. Необходимым условием возможности создания таких моделей является наличие полного набора данных как о внешних факторах (погода, агротехника), так и об индикаторах роста и развития растений, при этом отправной точкой является информация о прошлых данных полевых опытов [2]. Научный полевой опыт позволяет изучать вклад факторов в формирование урожая (севооборот, обработка почвы, удобрения и др.), обобщать полученные результаты, создавая модели [3, 4].
Вплоть до настоящего времени исследователи в области агрономии при разработке моделей ориентируются на классические методы однофакторного, и лишь в отдельных случаях многофакторного, дисперсионного анализа, используя рекомендации, изложенные еще в «докомпьютерную» эру в учебнике Б.А. Доспехова [5]. Но в связи с распространением компьютерной техники появились новые возможности. В вышедшем в 2013 г. учебнике для агрономических специальностей [6] отмечается необходимость компьютерной оценки данных научного полевого исследования. При этом, помимо широко распространенного табличного процессора MS-EXCEL, рекомендуются к использованию такие пакеты программ анализа данных, как SPSS, STATGRAPHICS Plus for Windows, STAtistica, предлагающие исследователям широкий спектр многомерных методов моделирования, основанных на алгоритмах регрессионного, дискриминантного, факторного, кластерного анализа. Однако в широкую практику использование указанных пакетов программ для анализа данных пока не вошло, обучение студентов-аграриев в отечественных вузах искусству моделирования по-прежнему ведется по методикам дисперсионного анализа или, в лучшем случае, универсального пакета MS-EXCEL. На актуальность «внедрения» новых технологий анализа данных в практику сельскохозяйственных исследований указывали различные авторы, в частности, В.М. Кузнецов [7]. Он отмечал, что «в большинстве работ российских исследователей-животноводов анализ экспериментальных и «полевых» данных… ограничивается расчетом средних значений и, в лучшем случае, их стандартных ошибок. Лишь в небольшом числе работ используется однофакторный дисперсионный анализ и очень редко – многофакторные обобщенные линейные модели» [7, с. 27].
В растениеводстве ситуация аналогичная. Лишь в немногих работах использованы компьютерные методики многофакторного многомерного дисперсионного анализа. Так, в работе [8] многофакторный многомерный дисперсионный анализ реализован с помощью процедуры обобщенной линейной модели пакета STAtistica, что позволило авторам данной работы получить ряд новых выводов по засоренности зерновых агроценозов, при этом, как правило, по всем выделяемым эффектам нулевые гипотезы отвергались с высокой доверительной вероятностью [8, с. 5].
Вышесказанное актуализирует наши исследования, направленные на адаптацию новых процедур получения моделей по результатам сельскохозяйственных экспериментов к специфике отрасли.
Цель исследования: исследование возможностей и эффективности применения одной из перспективных процедур дисперсионного анализа – обобщенной линейной модели – для разработки моделей полевых опытов. Особенность этой модели дисперсионного анализа заключается в том, что она ставит в соответствие результирующий показатель значениям воздействующих факторов, которые могут быть как количественными, так и качественными. В этом ее преимущество против регрессионных, в которых все предикторы, как правило, количественные. Еще одним преимуществом процедуры обобщенной линейной модели является возможность оценки статистической значимости эффектов и их доверительных границ, что обеспечивает надежность обоснования достоверности и значимости результатов полевых опытов.
Материалы и методы исследования
В исследовании нами использовалась одна из версий пакета статистических программ анализа данных общественных наук SPSS – версия 8.0 [9], а конкретнее, процедура «Обобщенная линейная модель» данного пакета. Прямое назначение данной процедуры – нахождение параметров модели, связывающей результирующую количественную переменную с двумя и более качественными (номинальными) переменными, однако команды процедуры «Общая линейная модель» позволяют выполнять и однофакторный дисперсионный анализ [10, 11]. В качестве примера использовали эмпирические данные полевых исследований по изучению влияния предшественников на продуктивность озимой пшеницы с применением различных норм минеральных удобрений, полученные в производственных условиях СПК «Русь» Знаменского района Орловской области [12]. Исследования проведены в 2006–2007 гг. по плану полного двухфакторного эксперимента ПФЭ 3×2: фактор А – предшественники: 1) кукуруза на зеленую массу, 2) горох на зерно, 3) ячмень; фактор В – нормы внесения удобрений: 1) 2 ц/га азофоски, 2) 4 ц/га азофоски. Объектом исследования являлся районированный в Орловской области сорт озимой пшеницы Московская 39, способный формировать зерно с высокими технологическими качествами. Опыты проводились в трехкратной повторности, однако обработке подвергали лишь средние данные по повторностям, тем самым воспроизводя ситуацию отсутствия первичных (сырых) данных полевых опытов.
Результаты исследования и их обсуждение
Методику двухфакторного дисперсионного анализа, реализуемую с помощью процедуры обобщенной линейной модели, рассмотрим на основе исходных данных по урожайности и качеству зерна озимой пшеницы сорта Московская 39, приведенных в табл. 1.
Таблица 1
Урожайность и качество зерна озимой пшеницы Московская 39 (в среднем за два года). Источник: [12, с. 30]
|
Предшественники |
Норма удобрений |
Урожайность, ц/га |
Содержание, % |
|
|
клейковины |
белка |
|||
|
1. Кукуруза |
1. 2 ц/га азофоски |
28,4 |
24,7 |
11,8 |
|
2. 4 ц/га азофоски |
33,5 |
26,1 |
12,5 |
|
|
2. Горох |
1. 2 ц/га азофоски |
34,2 |
26,8 |
13,2 |
|
2. 4 ц/га азофоски |
38,5 |
27,5 |
14,7 |
|
|
3. Ячмень |
1. 2 ц/га азофоски |
26,1 |
22,0 |
11,3 |
|
2. 4 ц/га азофоски |
29,3 |
23,6 |
12,7 |
|
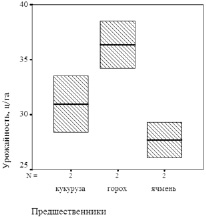
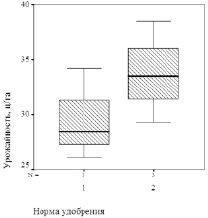
На первом этапе методики проводим визуальный анализ диаграмм Тьюки по предшественникам и норме удобрений (рис. 1).
а) б)
Рис. 1. Урожайность озимой пшеницы: а) в зависимости от предшественников; б) в зависимости от нормы азофоски (1 – 2 ц/га; 2 – 4 ц/га)
Из рис. 1, а, видно, что урожайность озимой пшеницы по гороху превосходит урожайность по ячменю и кукурузе, однако по кукурузе и ячменю наблюдается перекрытие диапазонов изменения показателя. По норме удобрений также наблюдается перекрытие значений показателя, хотя медианы при этом различаются – рис. 1, б.
На следующем этапе проводим оценку статистической значимости различия урожайности по предшественникам и норме удобрений «в целом» в процедуре «Обобщенная линейная модель», используя модель двухфакторного дисперсионного анализа (табл. 2).
Таблица 2
Тест межсубъектных эффектов
|
Источник изменчивости |
Сумма квадратов |
Ст. св. |
Средний квадрат |
F-критерий |
Значимость |
|
Исправленная модель |
102,823 |
3 |
34,274 |
75,328 |
0,013 |
|
Постоянная |
6016,667 |
1 |
6016,667 |
13223,443 |
0,000 |
|
Предшественник |
76,363 |
2 |
38,182 |
83,916 |
0,012 |
|
Удобрение |
26,460 |
1 |
26,460 |
58,154 |
0,017 |
|
Ошибка |
0,910 |
2 |
0,455 |
||
|
Сумма |
6120,400 |
6 |
|||
|
Исправленная сумма |
103,733 |
5 |
Из табл. 2 следует, что оба фактора – предшественники и норма удобрения – статистически значимы на уровне не хуже 0,05. Это позволяет признать адекватной модель
yij = m0 + ai + bj + eij
и оценить ее параметры (табл. 3). В этой модели: yij – наблюдаемое значение выходной переменной y (урожайность) на i-м уровне фактора «предшественник» и j-м уровне фактора «норма удобрения»; m0 – оценка свободного коэффициента модели; ai и bj – оценки главных эффектов; eij – случайная ошибка.
Таблица 3
МНК-оценки параметров двухфакторной модели влияния предшественника и нормы удобрения на урожайность озимой пшеницы
|
Параметр |
B |
Стд. ошибка |
t |
Значимость |
95 % доверительный интервал |
|
|
нижняя граница |
нижняя граница |
|||||
|
Постоянная |
29,800 |
0,551 |
54,107 |
0,000 |
27,430 |
32,170 |
|
[ПРЕДШЕСТ=1] |
3,250 |
0,675 |
4,818 |
0,040 |
0,348 |
6,152 |
|
[ПРЕДШЕСТ=2] |
8,650 |
0,675 |
12,824 |
0,006 |
5,748 |
11,552 |
|
[ПРЕДШЕСТ=3] |
0 |
, |
, |
, |
, |
, |
|
[УДОБРЕНИ=1] |
–4,200 |
0,551 |
–7,626 |
0,017 |
–6,570 |
–1,830 |
|
[УДОБРЕНИ=2] |
0 |
, |
, |
, |
, |
, |
Поясним табл. 3. В ней постоянная m0 = 29,8 ц/га, эффекты предшественника 3 (ячмень) и нормы удобрения 2 (4 ц/га азофоски) приняты за нулевые. Эффекты других предшественников и нормы удобрения отсчитываются уже от этого уровня; так, урожайность озимой пшеницы по предшественнику 2 (гороху) характеризуется добавкой a2=8,65 ц/га. Значения 95 %-ного доверительного интервала всех эффектов не включают в себя нуль, что свидетельствует о статистической значимости параметров модели.
Дополнительную информацию о значимости разности средних дают табл. 4 множественных сравнений и табл 5 однородных подгрупп предшественников, полученные при использовании критерия Тьюки.
Таблица 4
Апостериорные парные сравнения средних по критерию Тьюки
|
(I) Предшественники |
(J) Предшественники |
Средняя разность (I–J) |
Стд. ошибка |
Знач. (2-сторон) |
95 % доверительный интервал |
|
|
нижняя граница |
верхняя граница |
|||||
|
Кукуруза |
Горох |
–5,400 |
0,6745 |
0,028 |
–9,374 |
–1,426 |
|
Ячмень |
3,250 |
0,6745 |
0,073 |
–0,724 |
7,224 |
|
|
Горох |
Кукуруза |
5,400 |
0,6745 |
0,028 |
1,426 |
9,374 |
|
Ячмень |
8,650 |
0,6745 |
0,011 |
4,676 |
12,624 |
|
|
Ячмень |
Кукуруза |
–3,250 |
0,6745 |
0,073 |
–7,224 |
0,724 |
|
Горох |
–8,650 |
0,6745 |
0,011 |
–12,624 |
–4,676 |
|
Согласно табл. 4, статистически значимыми на уровне надежности не хуже 95 % могут быть приняты разности урожайности озимой пшеницы по предшественнику гороху с урожайностью по предшественникам ячменю и кукурузе, так как соответствующие значения 95 %-ного доверительного интервала не включают в себя нуль. Напротив, разность урожайности озимой пшеницы по предшественникам ячменю и кукурузе статистически значима на уровне 0,073, превышающем нормативную величину 0,05; кроме того, доверительный интервал данной разности включает в себя нуль.
С этими результатами согласуются данные табл. 5: горох образует самостоятельную подгруппу, тогда как ячмень и кукуруза входят в общую подгруппу 1.
Таблица 5
Однородные подгруппы предшественников по критерию Тьюки (уровень значимости критерия различия между подгруппами р = 0,05)
|
Предшественники |
N |
Урожайность озимой пшеницы, ц/га |
|
|
1 |
2 |
||
|
Ячмень |
2 |
27,700 |
|
|
Кукуруза |
2 |
30,950 |
|
|
Горох |
2 |
36,350 |
|
|
Уровень значимости критерия различия в подгруппе |
0,073 |
1,000 |
|
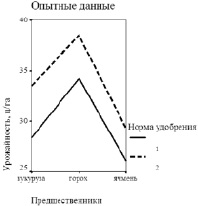
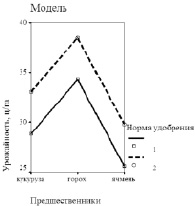
Наглядное представление о качестве прогноза урожайности по двухфакторной модели дает рис. 2: видно, что расчетные данные лишь немного отличаются от опытных.
Следует особо отметить, что проведенный выше анализ выполнен для средних, без учета данных по повторностям. Именно этим объясняется довольно высокое значение стандартной ошибки разностей урожайности – 0,67 ц/га. Соответственно этому наблюдается значительная ширина 95 %-ных доверительных интервалов эффектов прибавки урожайности от агротехнических факторов. Так, при средней прибавке урожайности озимой пшеницы по предшественнику гороху относительно предшественника кукурузы 5,40 ц/га доверительный интервал составляет от 1,43 до 9,37 ц/га, а относительно предшественника ячменя – 8,65 ц/га с 95 %-ным доверительным интервалом от 4,68 до 12,62 ц/га. Впрочем, эта ситуация вполне соответствует значительной изменчивости условий возделывания большинства сельскохозяйственных культур.
а) б)
Рис. 2. Урожайность озимой пшеницы в зависимости от предшественников и нормы азофоски: а) опытные данные; б) расчет по двухфакторной модели
а) б)
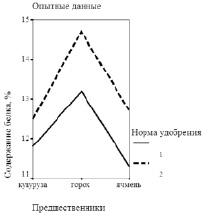
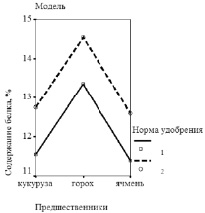
Рис. 3. Содержание в зерне озимой пшеницы сырого белка в зависимости от предшественников и нормы азофоски: а) опытные данные; б) расчет по двухфакторной модели
а) б)
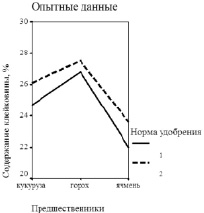
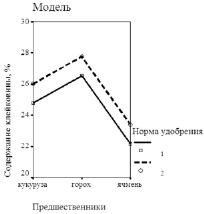
Рис. 4. Содержание в зерне озимой пшеницы клейковины в зависимости от предшественников и нормы азофоски: а) опытные данные; б) расчет по двухфакторной модели
Аналогично нами были получены двухфакторные модели влияния предшественников и норм удобрений на содержание в зерне озимой пшеницы сорта Московская 39 сырого белка и клейковины, объясняющие соответственно 97,3 % и 99,0 % общей дисперсии.
Согласно приведенным графикам, отражающим качество двухфакторных моделей (рис. 3, 4), установлено, что, так же как и на урожайность, предшественники оказывают более сильное влияние на оба показателя качества зерна, чем нормы удобрений, причем лучшие результаты достигаются при посеве озимой пшеницы по гороху.
Высокое качество полученных моделей подтверждается также близкими к единице значениями коэффициента детерминации R2: для модели урожайности R2 = 0,991, для содержания белка и клейковины 0,973 и 0,990 соответственно.
Заключение
Представленный пример показывает, что преимуществом использования процедуры обобщенной линейной модели для анализа результатов полевых опытов является возможность построения моделей по средним данным, в случае отсутствия информации по повторностям. Это позволяет строить модели также и по материалам публикаций, которые, как правило, содержат лишь средние данные, а результаты измерений по повторностям не приводятся.



