При проектировании схемы разработки месторождения используется построенная геолого-промысловая модель месторождения, основанная на структурно-фациальной и тектонической компонентах модели месторождения. Различная степень обеспеченности реальными данными, неполнота для отдельных измеренных и используемых при прогнозировании значений параметров геофизических исследований скважин (ГИС) приводит к тому, что различные фрагменты прогнозируемой модели определяются с различной степенью надежности. Неучет этих обстоятельств повышает технико-экономические риски принятия решений о проекте разработки залежей и требует объективной оценки меры информационной обеспеченности выполненных построений. Петрофизические модели обычно описываются регрессионными уравнениями, в которых сложно учесть неоднородность, нечеткость данных, присущих геолого-геофизическим параметрам. Решение этой задачи требует другого подхода и нового аппарата анализа данных.
Цель исследования: разработка способов построения функций принадлежности нечетких величин и нечетких отношений геолого-геофизических, промысловых параметров с использованием методов нечеткого моделирования, основы которых изложены в [1–3]. Это позволит оценивать меру неопределенности параметров при проведении прогноза и учитывать полученные результаты при разработке схем проектирования месторождений.
Материалы и методы исследования
Материалом для исследования являются геолого-геофизические, промысловые параметры, а методами исследования – аппарат теории нечетких множеств [4, 5].
Результаты исследования и их обсуждение
Первый этап прогнозирования параметров геологической модели – фазификация данных – на основе нечетких данных и нечетких отношений между переменными состоит в том, что экспериментальные данные о параметрах среды и петрофизические модели представляются в форме нечетких величин и нечетких отношений.
Фазификация отношений состоит в выражении зависимостей между нечеткими параметрами – переменными, в форме нечетких отношений. Исходными данными формирования функции принадлежности 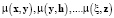 для отношения между нечеткими величинами
для отношения между нечеткими величинами 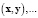 служат результаты измеренных пар значений
служат результаты измеренных пар значений 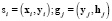 для всех из рассматриваемых отношений. Для определенности выберем задачу установления отношения между нечеткими величинами x и y на основе эксперимента
для всех из рассматриваемых отношений. Для определенности выберем задачу установления отношения между нечеткими величинами x и y на основе эксперимента 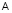 приведшего к результатам
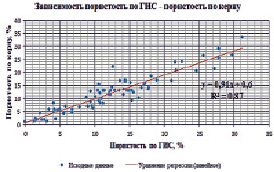
приведшего к результатам 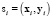 , где число измерений равно n. Рассмотрения автоматически переносятся на любые другие пары. Пусть, например, x – экспериментально измеренная пористость по данным ГИС, y – пористость того же образца по керну. Полигон данных
, где число измерений равно n. Рассмотрения автоматически переносятся на любые другие пары. Пусть, например, x – экспериментально измеренная пористость по данным ГИС, y – пористость того же образца по керну. Полигон данных 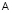 , полученных в результате измерений
, полученных в результате измерений 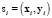 , приведен на рис. 1, а. Картой плотности данных, или полем рассеяния для связи между параметрами называется сетка, значений плотности данных в каждой ячейке вычисляемых по правилу
, приведен на рис. 1, а. Картой плотности данных, или полем рассеяния для связи между параметрами называется сетка, значений плотности данных в каждой ячейке вычисляемых по правилу
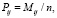 (1)
(1)
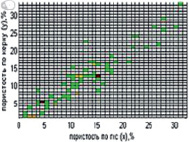
где Mij – количество значений, попавших в ячейку, а n – количество всех измеренных значений (рис. 1, б).

в)
Рис. 1. Полигон данных 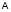 : а) зависимость «пористость по ГИС – пористость по керну» и соответствующая ей карта плотности; б) поле рассеяния для связи между параметрами; в) легенда по параметру количества данных, попавших в ячейку, г) легенда по максимальным значениям по оси Y на выбранном интервале по оси Х
: а) зависимость «пористость по ГИС – пористость по керну» и соответствующая ей карта плотности; б) поле рассеяния для связи между параметрами; в) легенда по параметру количества данных, попавших в ячейку, г) легенда по максимальным значениям по оси Y на выбранном интервале по оси Х
а)
б)
г)
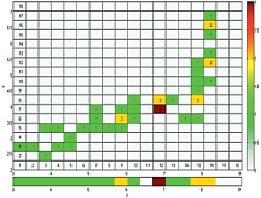
а)
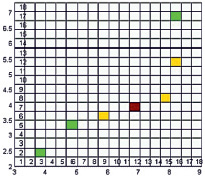
б)
Рис. 2. Сопоставление карты плотности (а) и карты источников плотности для поля рассеяния данных (б)
Выбор аналитического вида функции принадлежности одновременно означает формирование гипотезы о причинах рассеяния экспериментальных данных в облако, для которого, конечно, можно вычислить и центр, и разброс, но оно само по себе несет еще скрытую информацию о характере неоднородности среды, приведшей к рассеянию экспериментальных данных [6, 7]. Экспоненциальная модель для нахождения аналитического вида функции принадлежности определяется из уравнения диффузии в однородной бесконечной среде с заданными начальными условиями с использованием метода Грина. Среда состоит из совокупности частей, различающихся между собой одновременными наборами параметров 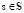 . Плотность концентрации элементов в этой смеси характеризуется функцией концентрации μ(s). Искомая функция принадлежности
. Плотность концентрации элементов в этой смеси характеризуется функцией концентрации μ(s). Искомая функция принадлежности 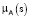 – это итог диффузии μ(s), происходящей с некоторым коэффициентом а, и длящейся некоторое время τ
– это итог диффузии μ(s), происходящей с некоторым коэффициентом а, и длящейся некоторое время τ 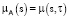 . Решение принимает вид
. Решение принимает вид
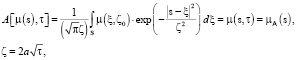 (2)
(2)
ζ – эффективный параметр рассеяния для моделируемой функции принадлежности 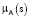 ;
; 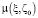 – стартовое распределение источников информации, которому приписывается стартовый параметр рассеяния ζ0, относительно которого далее происходит выбор эффективного параметра рассеяния. Практический выбор
– стартовое распределение источников информации, которому приписывается стартовый параметр рассеяния ζ0, относительно которого далее происходит выбор эффективного параметра рассеяния. Практический выбор 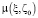 , определен плотностью источников поля рассеяния.
, определен плотностью источников поля рассеяния.
Определим значения 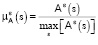 по введенной сетке
по введенной сетке 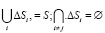 . Функция
. Функция 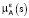 суть значения в ячейках ΔSi нормированной функции рассеяния
суть значения в ячейках ΔSi нормированной функции рассеяния 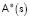 . Таким образом, правая часть в (2) – это набор дискретных значений по ячейкам ΔSi, так же как и искомая
. Таким образом, правая часть в (2) – это набор дискретных значений по ячейкам ΔSi, так же как и искомая 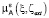 . Принцип компактификации источников формулируется как выбор такого распределения источников
. Принцип компактификации источников формулируется как выбор такого распределения источников 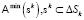 и ей соответствующей функции принадлежности с
и ей соответствующей функции принадлежности с 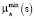 , которые характеризуются минимальным числом K носителей (ненулевых значений
, которые характеризуются минимальным числом K носителей (ненулевых значений 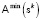 в покрытии ΔSk), выбранной сеткой фазового пространства S, при условии приближенного выполнения соотношения (2). Это соответствует задаче целочисленного программирования:
в покрытии ΔSk), выбранной сеткой фазового пространства S, при условии приближенного выполнения соотношения (2). Это соответствует задаче целочисленного программирования:
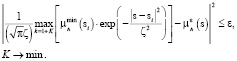 (3)
(3)
Ее решение выполняется численно, перебором значений K от максимального, определенного построенными значениями 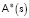 , в ячейках сетки
, в ячейках сетки 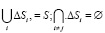 , до минимального, при котором условие неравенства еще выполняется. Результат решения
, до минимального, при котором условие неравенства еще выполняется. Результат решения 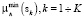 называется картой плотности источников данных или полем источников данных. Алгоритм построения карты источников, плотности данных называется алгоритмом сжатия информации на основе уравнения (2). Исходя из карты плотности, источников поля рассеяния, могут быть получены параметризованные эффективным параметром рассеяния ζ модели функции принадлежности для характеристики нечеткого отношения.
называется картой плотности источников данных или полем источников данных. Алгоритм построения карты источников, плотности данных называется алгоритмом сжатия информации на основе уравнения (2). Исходя из карты плотности, источников поля рассеяния, могут быть получены параметризованные эффективным параметром рассеяния ζ модели функции принадлежности для характеристики нечеткого отношения.
Для приведенного на рис. 1, а, примера полигона данных и ему соответствующей карты плотности данных (поля рассеяния), его сопоставление с соответствующей картой плотности источников поля рассеяния приведено на рис. 2.
Переход к плотности источников поля рассеяния позволяет существенно снизить размерность величин.
Основываясь на полученной карте плотности источников 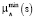 , по формуле
, по формуле
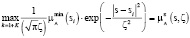 (4)
(4)
рассчитываются параметризованные эффективным параметром поглощения ζ функции принадлежности 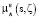 для исходных данных
для исходных данных 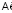 , соответствующие разной степени рассеянности, контролируемой значением коэффициента (параметра) эффективного рассеяния ζ. Выполняя моделирование функции принадлежности на фазовом пространстве S, по параметру эффективного рассеяния ζ, на основе суперпозиции функций принадлежности, построенных по полю рассеяния с минимальным числом носителей, следует учитывать изменчивость параметра ζ, в зависимости от относительной плотности источника в ячейках для поля рассеяния
, соответствующие разной степени рассеянности, контролируемой значением коэффициента (параметра) эффективного рассеяния ζ. Выполняя моделирование функции принадлежности на фазовом пространстве S, по параметру эффективного рассеяния ζ, на основе суперпозиции функций принадлежности, построенных по полю рассеяния с минимальным числом носителей, следует учитывать изменчивость параметра ζ, в зависимости от относительной плотности источника в ячейках для поля рассеяния 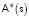 . В этом случае соотношение (4) должно быть обобщено:
. В этом случае соотношение (4) должно быть обобщено:
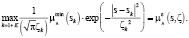 (5)
(5)
При выборе ζ следует ориентироваться на то, чтобы поле рассеяния для моделируемой функции принадлежности покрывает исходный полигон данных на 90 %. Мера покрытия полем рассеяния исходного полигона служит критерием для подбора эффективного параметра рассеяния. Многочисленные эксперименты показали, что оптимально в качестве функции принадлежности брать именно экспоненциальный вид [6, 7].
Фазификация входных данных состоит в построении функций принадлежности 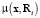 для исходного параметра – аргумента x в локальных интервалах Ri, в которых будет выполняться прогнозирование на основе нечеткой петрофизической модели. Если измерена серия значений
для исходного параметра – аргумента x в локальных интервалах Ri, в которых будет выполняться прогнозирование на основе нечеткой петрофизической модели. Если измерена серия значений 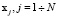 параметров, в одной и той же пространственной точке, то функция принадлежности
параметров, в одной и той же пространственной точке, то функция принадлежности 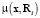 для x в точке Ri примет вид
для x в точке Ri примет вид
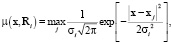 (6)
(6)
где σi – оцененная погрешность измерений параметра x в точках пространства Ri. Схема фазификации соответствует объективному представлению данных ГИС в форме функций принадлежности, отражающих структуру и достоверность информации (рис. 3).
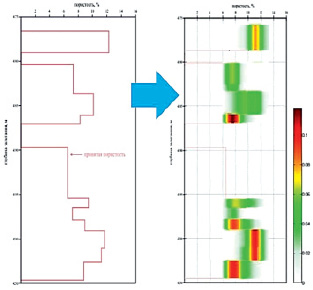
Рис. 3. Преобразование прогнозных данных по ГИС в функции принадлежности
Пространственное положение единицы прогноза – пропластка, либо залежи, для которой приняты построенные функции принадлежности отношений и функции принадлежности параметра x, служащего основанием для прогноза, контролируется пространственной переменной Ri. Она не участвует в вычислительных формулах, проявляясь лишь в оценке погрешности измеренных параметров, отнесённых именно к этой точке. Пространственное положение прогнозных параметров далее используется при интерполяции моделей.
Прогнозный параметр – это параметр физико-геологической модели, который прогнозируется на основании входных данных и имеющихся связей. Это может быть пористость, проницаемость, нефтегазонасыщенность или что-либо иное. Построение графа прогноза начальных – промежуточных – прогнозных параметров является предметом отдельной статьи.
Заключение
Таким образом, результатом исследований является разработанный теоретический аппарат для построения функций принадлежности геолого-геофизических, промысловых параметров для учета неопределенности при проведении дальнейшего прогноза. Это позволит снизить технико-экономические риски принятия решений при проектировании схемы разработки месторождений.



