Для зоны активного межплитного взаимодействия окраины Восточной Азии в литературе описаны многочисленные крупные сдвиговые структуры различной глубины заложения [1–3], представляющие собой сдвиги режима трансформной континентальной окраины, а также границы крупных блоков земной коры, террейнов и супертеррейнов. При этом детали строения синсдиговых структур и зон, а также особенности их формирования могут опускаться в масштабе рассмотрения. В пределах Сихотэ-Алинского складчатого пояса – протяженной надсубдукционной структуры обрамления Восточной Азии, рассматриваемой в пределах Приморского и Хабаровского краев, располагаются скопления рудного вещества, а также благородных металлов, ассоциированные с гранитоидным магматизмом (Лермонтовское (W), Партизанское (TR, W), Тигриное (Sn, W), Многовершинное (Au-Ag), Салют (Au-Ag) и другие). Численные расчеты полей напряжений участков их локализации интрузий – источников рудного вещества могут способствовать проведению на их основе комплекса стуктурно-парагенетических признаков региональных исторических и минерагенических исследований и создание предпосылок прогноза зон коры, благоприятных для процессов рудогенеза.
Целью настоящего исследования, включающего моделирование тектонопар сдвигов, является формирование представлений об ожидаемых деформациях горных пород в межсдвиговых зонах и их морфологическом выражении на плоскости для дальнейшего использования в технологиях дистанционного зондирования Земли. Дешифрирование космических снимков горно-складчатых областей и интерпретация получаемых тектонических схем в ряде случаев требует рассмотрения кинематики зон сжатия или растяжения, ограниченных системами субпараллельных сдвигов. Численное моделирование может дать сведения о положении и направлении смещения межсдвиговой зоны при различных скоростях и амплитудах перемещения крыльев сдвигов. В то время как имеющиеся традиционные представления о тектонопарах разрывных структур позволяют рассуждать о строении межсдвиговых зон лишь качественно, численные модели предоставляют количественные сведения с возможностью имплементации результатов для конкретной геологической обстановки исследуемой территории.
Материалы и методы исследования
Анализ структурного паттерна территории, полученного при обработке дистанционного космического изображения, требует выяснения его генезиса, главных направлений трещиноватости и роли действующих сил. Для описания региональной тектоники при значительных температурах и давлении, а также длительном времени воздействия уместно говорить о реологическом процессе. В этом случае твердое вещество рассматривается как очень вязкая жидкость, текущая с низкой скоростью в течение длительного времени. В синсдвиговых зонах Сихотэ-Алиня описаны (например, [4]) флюидальные текстуры тектонической брекчии. При этом авторами [4] указывается, что проницаемость породы для рудоносных растворов присутствовала именно на этапе вязкопластического течения субстрата.
Постановка задачи моделирования производится следующим образом. Производная поля деформации u по времени (производная Лагранжа) является вектором скорости смещения (течения)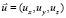 
таким образом, что
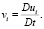(1)
Тензор деформации может быть представлен в виде градиента деформации [5]:
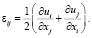(2)
Тензор скорости деформации является производной деформации по времени:
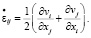(3)
Деформация непрерывной среды является следствием изменений баланса действующих внешних и внутренних сил. Для сопоставления этих сил и вызываемых ими деформаций используются уравнения сохранения импульса непрерывной среды в гравитационном поле, соответственно:
Эйлера:
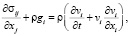(4)
Лагранжа:
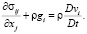(5)
Сохранение импульса жидкости в поле силы тяжести описывается уравнением движения Навье – Стокса:
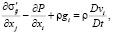(6)
где σ´ij – девиаторное напряжение, выражающееся как
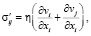(7)
где η – вязкость среды.
Конечно-разностное представление уравнений импульса и неразрывности может быть сформулировано на плоскости без учета гравитационной компоненты [5, Eq. 7.18]:
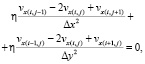(8)
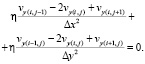(9)
Уравнения (10)–(11) используются для нахождения значений компонентов скорости вязко-пластичного течения вещества vx и vy методом конечных разностей (МКР) в среде научных и инженерных расчетов и программирования Mathworks Matlab (рис. 1).
Рис. 1. Нахождение значений компонента скорости vy для внутренних и граничных узлов МКР в Matlab
Для решения этой задачи на моделируемой плоскости в программу необходимо ввести входные параметры: значения динамической вязкости и плотности вещества (например, отсюда [6, таблица B. 5]), направление, время и амплитуду перемещения по разлому. Для линии разлома на горизонтальной плоскости задаются краевые значения компонентов скорости сдвигового перемещения на крыльях.
Ортогональные компоненты перемещения рассчитываются аналитически:
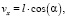(10)
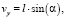(11)
где α – угол ориентации разлома на плоскости, l – амплитуда смещения по разлому.
Результаты исследования и их обсуждение
Рассматриваемая модель представляет интерес для анализа кинематики зон, сопровождающих параллельные разломы как собственно трансформного, так и субдукционного тектонических режимов, описанных на активных континентальных окраинах. Моделирование двух параллельных равноамплитудных сдвигов, выполненное в Matlab описанным выше способом, позволяет оценить кинематику и распределение напряжений и деформаций на плоскости (рис. 2).
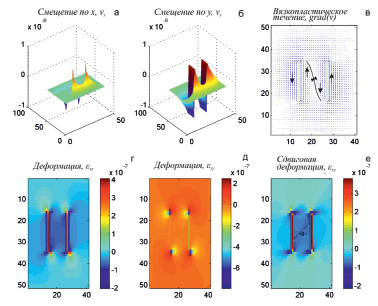
Рис. 2. Кинематика модели системы параллельных левосторонних сдвигов: a – vx компонента; б – vy компонента; в – градиент перемещения вещества и формирования зоны косого сдвига; г, д – ортогональные компоненты деформации εxx, εyy; е – сдвиговая компонента деформации εxy (стрелкой показано вероятное простирание трещин растяжения)
Анализ распределения направлений вязкопластического течения вещества позволяет установить зоны S-образных дислокаций в пространстве между сдвигами (рис. 2, в). Показано ортогональное сдвигу простирание трещин растяжения (рис. 2, е).
В своей обзорной работе [7, с. 156] авторы приводят характеристику трещиноватого паттерна левосдвиговой зоны. Для нашей модели можно предположить наличие близкой картины и в приложении к глубинному Центральному Сихотэ-Алинскому разлому – главному сдвигу в осевой части Сихотэ-Алинского складчатого сооружения. Формирование зоны противотечения внутри пространства между параллельными сдвигами приводит к формированию растяжения, сопряженного со сдвигом (транстенсии).
Анализ устойчивости модели проводится изменением исходных значений скорости (амплитуды) перемещений по левому и правому разлому. Для этого задавались значения скорости смещения 25 км и 10 км за 1 млн лет. При моделировании осевая транстенсионная зона смещается в сторону разлома с меньшей скоростью перемещения, вызывая ее асимметрию (рис. 3, a–в). В соответствии с [7], для осевой зоны сдвига характерны диагональные направления трещин сдвига и ортогональные – растяжения (рис. 3, г).
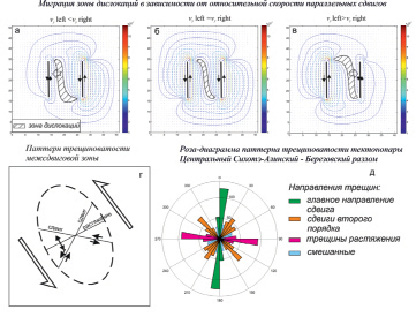
Рис. 3. Кинематика и положение межсдвиговой зоны: а–в – асимметрия транстенсионной зоны при различных соотношениях скорости смешения по разломам тектонопары; г – паттерн трещин растяжения (отрыва) и сдвига зоны растяжения; д – роза-диаграмма паттерна трещиноватости, полученная для тестовой площади
Таким образом, в межсдвиговом пространстве субпараллельных левых сдвигов формируется транстенсионная правосдвиговая зона. Правые сдвиги осложняются наличием растяжений, бассейновых структур («pull-apart») и полей трещиноватых, меланжированных и милонитизированных пород, проницаемых для магм и флюидов [7].
Свидетельством наличия режима транстенсионных правосдвиговых зон в структуре Журавлевского террейна Сихотэ-Алинского горно-складчатого пояса могут являться устойчивые в течение геологической истории характерные S-образные паттерны зон сопряжения крупных субпараллельных сдвигов, осложненные многоактным интрузивным магматизмом орогенного этапа [8]. Дешифрирование и учет линеаментов [9] на данном участке показывает характерную картину: главные направления трещиноватости осложняются структурами растяжения и сдвига второго порядка (рис. 3, д). В свою очередь, подтвержденное наличие транстенсионного правосдвигового режима на площади может явиться основанием для прогноза на ней ассоциированных месторождений: скарновых, грейзеновых, жильно-метасоматических и медно-порфировых.
Выводы
Синтез используемой численной модели и технологий обработки дистанционного изображения (включающих линеаментный анализ и построение роз-диаграмм трещиноватости) позволяет описать и интерпретировать наблюдаемую картину сложной зоны дислокаций систем параллельных разломов. Паттерны трещиноватости дистанционного изображения, дополненные данными численного геодинамического моделирования, могут рассматриваться в качестве прогнозно-поискового признака месторождений полезных ископаемых межсдвиговых зон. Компьютерное моделирование тектонопар лево- и правосторонних сдвигов может применяться для описания и прогноза зон транстенсии и транспрессии. Площади межсдвиговой транстенсии (растяжения) исключительно перспективны для выяснения генезиса депрессий осадочных бассейнов и зон внедрения интрузивных тел.