Физические процессы, протекающие в атмосфере, формируют погоду и климат, участвуют в формировании рельефа, влияют на инфраструктуру, жизнь и здоровье людей. К таким процессам относятся и изменения температуры воздуха при кондуктивном и радиационном теплообмене. Актуальной проблемой, обсуждаемой в настоящее время, является глобальное изменение климата, которое привязывают к природным причинам [1, 2], а также к антропогенной деятельности [3, 4]. Как глобальное похолодание, так и потепление имеют потенциальные опасности в масштабе всей планеты: оледенение рек, снижение пригодных для открытого земледелия зон, повышение интенсивности движения льда в океане, несущее опасность судоходству, распространение мерзлоты на территории, интенсивно используемой в аграрной, животноводческой отраслях, и, например, лесозаготовках, смена биоценозов в сторону обеднения или же, в противоположном случае, интенсивное таяние льдов и вечной мерзлоты, подъем уровня океана и ущерб для береговых, островных и других зон, при их малом или вообще отрицательном возвышении над уровнем моря и многое другое. Следует отметить, что температура воздуха, наряду с осадками, входит в основные климатические показатели [5–7].
В связи с этим особое внимание уделяется предупреждениям о сложившихся опасных для сельскохозяйственных культур агрометеорологических условиях – засухах, суховеях, заморозках и т.д. в летний период, и угрозе повреждений озимых культур от вымерзания, выпревания, ледяной корки в зимний период. Для оценки урожайности чрезвычайно важен и ход температуры в целом за вегетационный период. Чтобы оценить процессы, происходящие с ростом урбанизации для земледелия в пределах зоны влияния городской среды, требуется усовершенствовать стандартные методы обработки метеорологических данных.
Цель исследования: развитие и совершенствование метода исследований многолетнего хода температуры воздуха, с использованием таких величин как годовая средняя температура воздуха для выбранной местности, максимальная абсолютная температура воздуха, среднесуточная амплитуда температуры самого холодного месяца, среднесуточная амплитуда температуры самого теплого месяца года, добавлением варианта получения данных о модах частот повторяемости значений температуры воздуха.
Материалы и методы исследования
Температура воздуха – это крайне изменчивая характеристика атмосферы, она сильно изменяется по пространству и во времени. Суточный ход температуры воздуха при этом достаточно четко выражен и имеет в ясную погоду периодический характер. Данная закономерность хорошо видна при осреднении результатов многолетних наблюдений, но в рядах непосредственных измерений может нарушаться при пасмурной погоде, выпадении осадков, адвекции теплоты или холода. Непериодические вариации температурного режима воздушных масс чаще всего встречаются и достигают максимальных значений отклонений в умеренных широтах, это объясняется их связью с циклонической деятельностью, местными ветрами, тепловыми аномалиями [7–9]. Восходу Солнца соответствуют минимальные значения температуры, а соответственно, к 14–15 ч наблюдаются пики ее максимума. Подстилающая поверхность поглощает тепло, которое передается приземному слою воздуха не мгновенно, происходит некоторое запаздывание понижения и повышения температуры атмосферного воздуха по сравнению с изменениями температуры поверхности. В прилегающем к поверхности земли слое атмосферы суточный и годовой ход температуры воздуха определяют по значению температуры на уровне двух метров. Этот ход в основном обусловлен ходом температуры поверхности Земли. Особенности хода температуры атмосферного воздуха определяются значениями экстремумов. Разность между наибольшей и наименьшей температурами называют амплитудой хода температуры атмосферного воздуха. Эта амплитуда меняется: в зависимости от характера подстилающей поверхности, по сезонам года, по широте, от наличия облачности и ее типа, и в зависимости от орографии местности. Температура воздуха с высотой понижается по сухой или влажной адиабате, поэтому равнинные и горные территории, расположенные вдоль одной широты, имеют неодинаковую среднюю температуру воздуха. В горах температура существенно ниже [6, 10].
Температура атмосферного воздуха изменяется и в годовом ходе: среднемесячные температуры летом выше, зимой – ниже. Размах для годового хода – это есть отклонение среднемесячных температур наиболее жаркого и наиболее холодного месяцев. Вариация между абсолютным максимумом и абсолютным минимумом годовых температур воздуха, имевших место в течение контрольного года – это абсолютная годовая амплитуда температуры. На нее воздействуют:
– географическая широта: минимальный размах присущ зоне экватора, а с увеличением широты мезорайона амплитуда растет, принимая максимальные значения в южных полярных широтах, и в умеренных северных из-за слабого прогревания поверхности в теплый период для Субарктики и Арктики;
– высота места над уровнем моря: с ростом высоты над уровнем моря размах уменьшается;
– циркуляция воздушных масс и соответственно годовой ход облачности: поскольку зимой облачности нет, то средняя температура самого холодного месяца снижается, летом отсутствие облачности увеличивает среднюю температуру самого жаркого месяца;
– расстояние от моря: минимальные годовые амплитуды температуры воздуха имеют место над поверхностью крупных водоемов и характерны больше для морского климата, над поверхностью суши наблюдаются значительные амплитуды годовых значений температуры воздуха, характерные так же для континентального климата.
– погодные условия: туман, дождь и др.
Таким образом, температура воздуха – величина, понимание особенностей, динамики которой особенно важно для транспорта и сельского хозяйства.
Для анализа Федеральным государственным бюджетным учреждением «Северо-Кавказское управление по гидрометеорологии и мониторингу окружающей среды» был предоставлен 15-летний интервал метеорологических измерений температуры воздуха в г. Нальчике с осреднением за трехчасовые интервалы по данным таблицы метеорологических наблюдений с 2928 измерениями для високосных и 2920 для обычных лет. Микроклимат городской среды неизбежно оказывает влияние на значение всех метеорологических характеристик, наблюдаемых на метеостанциях в пределах городской территории. Диаграмма размаха, в предположении о нормальности распределения температуры воздуха в г. Нальчике, с осреднением за трехчасовые интервалы, представлена на рис. 1.
Гистограмма распределения частоты представляет собой эмпирическую функцию распределения. Из гистограммы распределения частоты можно определить модальное значение, то есть значение, наиболее часто встречающееся в ряде наблюдений. Промежуток времени с 2003 по 2017 г., как известно, отличался достаточно противоречивыми тенденциями динамики значений приземной температуры воздуха, для объяснения этого требуются детальные исследования. Результаты статистической обработки данных измерений приземной температуры воздуха за 2003–2017 г. представлены в табл. 1. Мода оценивается как значение среднегодовой температуры воздуха в центре интервала, для которого определяется максимум частоты.
Оценим частоту (повторяемость) yi, как число членов выборки, попавших в каждый интервал 0,5 °С (рис. 2).
Основными статистическими характеристиками для дифференциальных кривых распределения параметров по встречаемости являются: среднее значение, медиана и мода распределений (рис. 3).
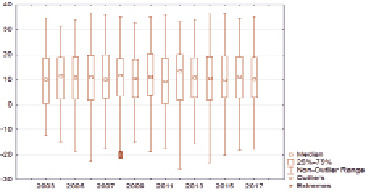
Рис. 1. Диаграмма размаха в предположении о нормальности распределения
Таблица 1
Результаты статистической обработки данных измерений приземной температуры воздуха за 2003–2017 гг.
|
Параметры |
Годы |
||||||
|
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
|
Среднее |
9,966 |
10,799 |
10,824 |
10,731 |
11,369 |
10,426 |
10,673 |
|
Медиана |
10,1 |
11,45 |
10,8 |
11 |
10,2 |
11,6 |
10,5 |
|
Мода |
–0,70 |
19,5 |
–0,7 |
0,7 |
1,3 |
15,0 |
4,0 |
|
Ст. откл. |
10,197 |
9,436 |
10,080 |
11,158 |
10,417 |
10,748 |
9,157 |
|
Минимум |
–12,5 |
–14,7 |
–18,7 |
–22,7 |
–17,7 |
–21,1 |
–15,2 |
|
Максимум |
34,7 |
31,5 |
34 |
36,8 |
36 |
35,2 |
32,5 |
|
0,25-квантиль |
0,5 |
2,1 |
2,1 |
1,7 |
2,4 |
3,5 |
2,8 |
|
0,75-квантиль |
18,6 |
18,8 |
19,15 |
19,8 |
19,9 |
18,4 |
18 |
|
Окончание табл. 1 |
|||||||
|
Годы |
|||||||
|
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
|
11,715 |
9,648 |
10,760 |
10,960 |
10,429 |
11,146 |
10,712 |
10,884 |
|
11,1 |
9,3 |
13,6 |
10,8 |
10,5 |
10,05 |
11,2 |
10,3 |
|
5,5 |
–1,5 |
17,7 |
0,0 |
0,4 |
3,9 |
4,0 |
17,5 |
|
10,518 |
10,430 |
11,797 |
9,507 |
10,550 |
9,887 |
10,335 |
10,147 |
|
–18,8 |
–17,4 |
–25,8 |
–15,9 |
–23 |
–20,2 |
–18,1 |
–17,9 |
|
35,2 |
36 |
33,1 |
34 |
36,2 |
36,4 |
34,6 |
35,2 |
|
3,9 |
0,4 |
1,6 |
2,8 |
1,8 |
2,8 |
2,6 |
2,8 |
|
20,3 |
18,6 |
20,1 |
18,7 |
19,1 |
19,4 |
19,1 |
18,85 |
Результаты исследования и их обсуждение
Для распределения по Гауссу среднее, медиана и мода совпадают (рис. 3, а) [11]. Однако для бимодального распределения (рис. 3, б) среднее попадает между двумя интервалами распределения. При этом встречаемость значений параметра, равных среднему, очень мала. Медиана сдвинута в правую часть распределения, а сама дифференциальная кривая имеет две моды. Для выбранного примера большая мода соответствует положению максимума правой части распределения. Пример демонстрирует, что среднее, мода и медиана – совершенно разные параметры, которые совпадают или близки лишь в исключительных случаях [12].
Имея в наличии цифровую информацию о метеопараметрах, которая фиксируется метеостанцией с интервалом каждые три часа, а конкретно о температуре воздуха на высоте двух метров, можно построить не только частотные гистограммы, но и карту распределения частот встречаемости температуры воздуха за доступный период наблюдений (рис. 3), это так называемая диаграмма «водопад».
На рис. 4 хорошо видно, что распределение частот встречаемости температуры воздуха неодномодальное. Расчёт эмпирической функции распределения среднегодовой температуры воздуха и проверка её на соответствие нормальному закону распределения показали, что более оптимальным уравнением, описывающим экспериментальные данные вследствие их мультимодального распределения, является, например, аппроксимация данных просто суммой ряда функций Гаусса.
Данный подход называется Гауссовыми смесями, они представляют собой сумму распределений нормальной величины [11, 12].
Модель гауссовых смесей – это взвешенная сумма M компонент, она может быть представлена в виде выражения
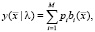(1)
где x – N-мерный вектор случайных величин; pi, i = 1, ..., M, – веса составляющих модели,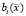 
, i = 1, ..., M, – функции плотности распределения компонентов модели. Здесь каждый компонент является N-мерной функцией Гаусса вида
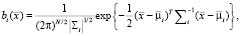(2)
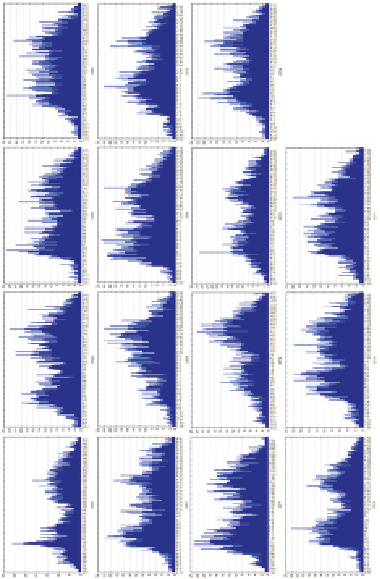
Рис. 2. Гистограммы частотного распределения температуры воздуха для каждого года (2003–2017 гг.) в пределах 15-летнего ряда измерений. Шкала температуры приведена в градусах Цельсия, а частота встречаемости в процентах
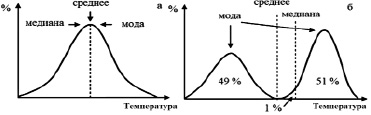
Рис. 3. Основные статистические характеристики при распределении по Гауссу (а) и бимодальном распределении (б)
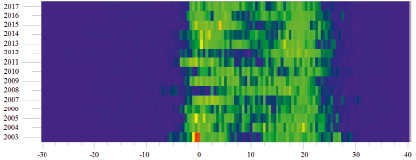
Рис. 4. Карта распределения частот встречаемости температуры воздуха от –30 до 40 °С за 2003–2017 гг.
Эти параметры можно записать в виде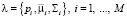 
. Исходя из этого модель гауссовых смесей определяется их весами смесей, векторами математического ожидания и ковариационными матрицами для каждого компонента модели.
Аппроксимируем эмпирические данные годовых частот распределения температуры воздуха как бимодальное распределение на основе гауссовой смеси получаем уравнение
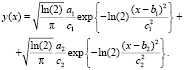(3)
Результаты аппроксимации годовых распределений частот температуры воздуха приведены в табл. 2.
На рис. 5 приведено сводное распределение частот температур в процентах, хорошо выражена особенность повторяемости температур воздуха в течение среднего года.
Наиболее часто встречающиеся значения температуры воздуха лежат в пределах от минус –10 до плюс 35 °С. Все частотные ряды, кроме 2008 г., имеют ярко выраженное бимодальное распределение. Четко выделяются годовой ритм изменений приземной температуры имеет некоторый подъем и сдвиг правого пика моды от холодных цветов к теплым 2003–2017 гг.
Таким образом, спектрально-временной анализ данных по изменчивости температуры воздуха в пределах года выявляет многомодальный характер частотности температур.
Новизна предлагаемого варианта выявления особенностей распределения частот внутригодовых значений температуры воздуха с помощью оценивания сдвигов мод по многолетним данным метеостанции Нальчик связана как с особенностями расположения метеостанции, ее высотой над уровнем моря, так и в особенности с местонахождением в пределах городской черты.
Таблица 2
Параметры уравнения аппроксимирующей функции
|
Параметры |
Годы |
||||||
|
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
|
a1 |
615,2 |
430,19 |
558,8 |
661,1 |
456,04 |
461,32 |
452,168 |
|
b1 |
0,548 |
0,3359 |
1,731 |
2,178 |
1,787 |
–0,032 |
1,7802 |
|
c1 |
4,585 |
3,9842 |
4,675 |
7,224 |
3,6638 |
9,5427 |
4,1634 |
|
a2 |
820,1 |
1038,4 |
874,1 |
769 |
1038,8 |
1000,4 |
1165,34 |
|
b2 |
18,04 |
16,421 |
18,0 |
19,40 |
17,996 |
15,921 |
17,397 |
|
c2 |
7,419 |
8,7555 |
8,024 |
7,928 |
11,547 |
9,1077 |
10,405 |
|
Окончание табл. 2 |
|||||||
|
Годы |
|||||||
|
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
|
827,61 |
616,99 |
529,62 |
651,76 |
594,82 |
676,1 |
544,10 |
653,21 |
|
5,577 |
0,2817 |
0,408 |
2,7839 |
1,645 |
3,009 |
1,9187 |
2,8856 |
|
7,4369 |
4,8744 |
7,3391 |
5,6794 |
5,1966 |
4,639 |
5,2219 |
5,9399 |
|
591,62 |
814,66 |
876,1 |
787,42 |
819,9 |
748 |
868,38 |
769,95 |
|
21,699 |
17,856 |
18,853 |
18,317 |
18,424 |
19,28 |
17,815 |
18,49 |
|
6,5971 |
7,7066 |
6,659 |
6,84 |
7,576 |
6,99 |
8,057 |
7,94 |
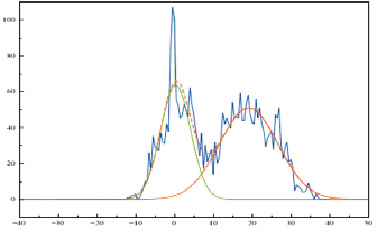
Рис. 5. Сводный график аппроксимирующих кривых. Шкала встречаемости приведена в виде повторяемости средних трехчасовых значений (раз за год)
Выводы
Для полноты представления о годовом ходе температуры воздуха предложено использовать помимо таких величин, как годовая средняя температура атмосферного воздуха для выбранной местности, максимальная абсолютная температура воздуха, среднесуточная амплитуда температуры самого холодного месяца, среднесуточная амплитуда температуры самого теплого месяца года, также данные о модах частоты повторяемости значений температуры воздуха. Частотное распределение температуры воздуха рекомендуется определять на основании данных метеостанции не менее чем за пять лет.
Разработан вариант автоматизированного расчета предлагаемых параметров на основе данных таблиц метеорологических наблюдений УГМС.
На основании экспериментальных данных наблюдений обоснован расчетный вариант выявления особенностей распределения частот внутригодовых значений температуры воздуха с помощью оценивания сдвигов мод по многолетним данным метеостанции Нальчик. Данное приближение позволяет рассматривать сложные изменчивые процессы с помощью их более простого аналога, получаемого в результате аппроксимации. Например, легко определить, что в выбранном для примера промежутке динамика моды положительных температур показывает тенденцию к положительному сдвигу.
Планируется использование полученного расчетного варианта в составе программного обеспечения выделения основных мод температуры для создания обоснованного прогноза урожайности сельскохозяйственных культур в пригородном хозяйстве учитывающего эффект «теплового острова», сопровождающего рост города.
Полученные результаты могут применяться, чтобы оценить степень благоприятности агрометеорологических условий для выбранной сельскохозяйственной культуры, оценить устойчивые повторяемости температур для выбора оптимального вегетационного периода, его начала, окончания и продолжительности. Оценить выбросы, характеризующие заморозки и высокие повреждающие температуры.
Применение разработанного варианта имеет перспективы для углубления знаний о метеорологических характеристиках в задачах описания многомодальных спектров.