Решение некоторых задач обеспечения безопасности полетов требует знания высот расположения определенных температурных уровней в атмосфере, в том числе внутри облаков, особенно кучево-дождевых [1].
Наиболее точную информацию о распределении температуры по высотам в атмосфере можно получить при помощи вертикального температурно-ветрового зондирования. Поднимающиеся в свободном полете датчики температуры и влажности с достаточной точностью регистрируют указанные параметры [2].
Однако сеть радиозондировочных пунктов разрежена, запуски радиозондов дорогостоящи и осуществляются в фиксированные моменты времени два раза в сутки, что существенно снижает ценность информации температурного зондирования для оперативной оценки возможности грозообразования и вероятности обледенения в кучево-дождевой облачности.
Для определения высоты расположения изотермы 0 °С разработана методика [3], основанная не на контактном измерении температуры в облачности, а базирующаяся на регистрации с помощью искусственного спутника Земли радиационной температуры верхней границы облачности и на информации о температуре воздуха у поверхности земли. Результаты, полученные при помощи данной методики, сопоставимы с данными температурно-ветрового зондирования, но указанный подход позволяет оценить высоту расположения только уровня 0 °С.
Следовательно, необходим поиск новых путей получения информации о распределении температуры по высотам в кучево-дождевой облачности.
Известны адиабатические и неадиабатические модели конвекции. К числу адиабатических относят модель частицы. Согласно данной модели перегретый относительно окружающего объем воздуха поднимается под действием силы Архимеда по сухоадиабатическому закону. Температура рассматриваемого объема воздуха уменьшается благодаря адиабатическому расширению. После достижения уровня конденсации, где начинается образование облачных элементов, охлаждение происходит медленнее за счет выделяющейся теплоты конденсации. Воздействие силы плавучести и в результате подъем воздуха происходят до момента выравнивания температур поднимающегося и окружающего воздуха. Этот уровень называется уровнем конвекции, и ему соответствует верхняя граница конвективного облака [4].
Модель частицы не является идеальной, она не учитывает некоторых факторов, существующих объективно, поэтому результаты, полученные с ее помощью, отличаются от фактического состояния атмосферы. Данная работа призвана исследовать возможность использования модели частицы для восстановления вертикального профиля температуры в кучево-дождевой облачности.
Материалы и методы исследования
На начальном этапе работы в качестве альтернативного пути получения информации о распределении температуры в атмосфере с высотой рассматривались данные стандартной атмосферы и средние климатические показатели.
По двум независимым выборкам фактического материала, составленным за теплый период с мая по сентябрь для центра европейской части России, был проведен статистический анализ. Для изотермических уровней 0 °С, –10 °С и –20 °С были получены значения их средних высот, а также максимальных отклонений от среднего значения.
Анализ результатов позволил сделать вывод о наименьшей изменчивости высоты расположения определенной температуры в июле, то есть в середине исследуемого периода, и увеличении изменчивости к переходным периодам года. Объясняется данный факт тем, что в середине лета господствующие воздушные массы наиболее однотипны, тогда как весной и осенью воздух может приходить из различных широтных поясов. Кроме того, наименьшим постоянством обладает высота изотермы 0 °С из-за близости данного уровня к земной поверхности и существенного влияния ее прогрева.
Также было оценено сходство рассчитанных средних значений высот расположения изотерм с данными стандартной атмосферы.
Результаты свидетельствуют о максимальном сходстве высот всех изотерм в мае и наименьшем в июле. Указанная картина сложилась вследствие осреднения данных для стандартной атмосферы за весь год, тогда как альтернативные сведения получены только для теплого периода.
В результате можно сделать вывод о том, что фактически наблюдаемые значения высот расположения изотермических уровней имеют значительный разброс относительно полученного среднего. Минимальное несоответствие прослеживается в середине лета. В то же время в середине теплого периода наблюдается наименьшая согласованность данных стандартной атмосферы и расчетных средних высот.
Таким образом, информация стандартной атмосферы существенно отличается от фактического хода температуры воздуха, особенно для июля, что исключает возможность ее использования для решения задачи мониторинга кучево-дождевой облачности.
В данной работе предлагается использовать адиабатическую модель развития конвективного облака для оценки высоты расположения различных температурных уровней.
Алгоритм, описывающий модель конвекции, можно представить следующим образом [5].
Исходными данными являются атмосферное давление P0, температура воздуха T0, измеренные у земной поверхности, и высота нижней границы облаков Ннго, зарегистрированная также с поверхности земли.
Для работы модели необходима информация о температуре на уровне высоты нижней границы облачности, то есть на уровне конденсации (Ннго = Нук). Определяется температура на данном уровне при помощи выражения
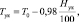 (1)
(1)
где 0,98 – величина, на которую температура изменяется в воздухе при его подъеме на высоту 100 м до момента начала конденсации водяного пара (сухоадиабатический вертикальный температурный градиент).
Атмосферное давление, входящее в параметры модели, находится на уровне конденсации при помощи барометрической формулы вида
 (2)
(2)
где g – ускорение свободного падения, Rc – удельная газовая постоянная сухого воздуха.
При помощи выражений (1) и (2) определены переменные величины, необходимые для дальнейшей реализации модели.
Вследствие того, что подъем воздуха выше уровня конденсации осуществляется с выделением скрытого тепла конденсации, температура его изменяется по влажноадиабатическому закону, не являющемуся линейным. Однако при незначительных изменениях высоты подъема облачного воздуха изменение его температуры можно описать при помощи влажноадиабатического градиента, считая его постоянным.
Следуя приведенному допущению, определим необходимые величины на уровне, находящемся выше уровня конденсации на 10 гПа. Высота может быть получена при помощи формулы Бабине:
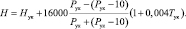 (3)
(3)
Температура рассчитывается при помощи формулы
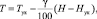 (4)
(4)
где γ – величина влажноадиабатического градиента, определяемого выражением
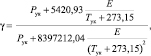 (5)
(5)
где Е представляет собой упругость водяного пара, находящегося в состоянии насыщения, на предыдущем уровне, то есть уровне конденсации. Находится при помощи выражения
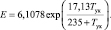 (6)
(6)
Зная температуру воздуха и высоту уровня в облаке, на котором давление ниже, чем на уровне конденсации на 10 гПа, можно при помощи выражений (3–6) аналогично рассчитать искомые величины (температуру воздуха и высоту его расположения) для всех вышележащих слоев облака до его верхней границы.
Отсутствие данных о высоте нижней границы облачности Ннго = Нук можно компенсировать информацией о температуре точки росы Td0, измеренной у поверхности земли. Зная P0, T0 и Td0, можно определить значения T и Td на уровне высоты нижней границы облачности с помощью выражений
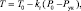 (7)
(7)
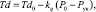 (8)
(8)
где kt и kq – значения средних угловых коэффициентов для сухих адиабат и изограмм.
Из выражений (7) и (8), учитывая то, что облачность начинает образовываться на высоте, где T становится равной Td, получаем выражение для нахождения давления на уровне конденсации
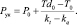 (9)
(9)
Используя значение Рук, при помощи формулы Бабине определяем высоту нижней границы облачности:
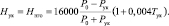 (10)
(10)
Далее, применяя полученные данные, с использованием приведенного ранее алгоритма определяется высота любого изотермического уровня в конвективном облаке.
Результаты исследования и их обсуждение
Следующим этапом в работе было испытание предлагаемого способа оценки высоты расположения любого изотермического уровня в конвективной облачности. По двум независимым выборкам исходных данных объемом 100 и 33 случая, состоящим из значений P0, T0 и Ннго, по приведенному выше алгоритму были рассчитаны высоты изотермических уровней 0 °С, –10 °С и –20 °С. Контрольным материалом для сравнения служили фактические данные радиозондирования атмосферы.
Ряды полученных значений высот изотерм длиной 100 случаев обозначим выборкой 1, а длиной 33 случая – выборкой 2. На рис. 1 и 2 графически представлены результаты сравнения фактических и рассчитанных при помощи модели значений высоты изотермы с номиналом 0 °С.
На графиках видно, что расчетные значения высоты изотермы меньше, чем фактические. Результаты, полученные для значений высот изотермических уровней –10 °С и –20 °С, аналогичны картине, представленной на рис. 1 и 2. Для количественной оценки данной разницы были рассчитаны величины отклонения расчетных значений высот изотерм от фактических. На рис. 3 и 4 представлены результаты для изотермического уровня –10 °С.
Из рис. 3 и 4 видно, что результаты эксперимента практически по всему объему выборок 1 и 2 меньше фактических, причем иногда существенно.
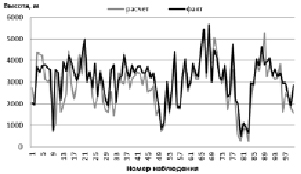
Рис. 1. Графики фактических и рассчитанных значений высоты нулевой изотермы по выборке 1
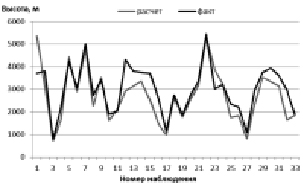
Рис. 2. Графики фактических и рассчитанных значений высоты нулевой изотермы по выборке 2
Статистические оценки качества предлагаемого способа
|
δ, м |
σ, м |
|
r |
|||||
|
Выборка 1 |
Выборка 2 |
Выборка 1 |
Выборка 2 |
Выборка 1 |
Выборка 2 |
Выборка 1 |
Выборка 2 |
|
|
0 °С |
494 |
157 |
713 |
366 |
–321 |
–97 |
0,81 |
0,84 |
|
–10 °С |
620 |
223 |
879 |
522 |
–508 |
–178 |
0,79 |
0,78 |
|
–20 °С |
774 |
261 |
1075 |
600 |
–670 |
–229 |
0,74 |
0,77 |
Для количественной оценки качества восстановления высот изотерм в конвективной облачности, то есть для оценки адекватности предлагаемого способа, были рассчитаны следующие статистические характеристики, рекомендуемые в [6]: средняя абсолютная ошибка δ, средняя квадратическая ошибка σ, средняя арифметическая (систематическая) ошибка 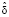 и коэффициент корреляции между рассчитанными и фактическими значениями высот одной и той же изотермы r. Значения статистических характеристик представлены в таблице.
и коэффициент корреляции между рассчитанными и фактическими значениями высот одной и той же изотермы r. Значения статистических характеристик представлены в таблице.
Как видно из таблицы, все рассчитанные для выборки 2 параметры лучше, чем для выборки 1, а также они ухудшаются от изотермы 0 °С к изотерме –20 °С. Первая закономерность связана, по всей видимости, с тем, что при увеличении объема выборки материала для испытаний увеличивается количество случаев с ошибками, приводящими к росту погрешностей. Вторая закономерность – с ухудшением качества определения высоты изотерм на больших высотах в конвективном облаке, что обусловлено несовершенством используемой модели.
Заключение
Таким образом, в данной работе предложен способ оценки высоты нахождения изотермических уровней в мощной конвективной облачности, основанный на использовании модели конвекции. Эксперимент, проведенный по итогам работы над способом, позволил рассчитать некоторые показатели успешности, которые дают возможность оценить адекватность, точность и устойчивость результатов предлагаемого подхода. Полученные результаты свидетельствуют о работоспособности данного способа, призванного без проведения контактных измерений оценить распределение температуры с высотой в мощной конвективной облачности. Однако из-за отдельных значительных ошибок и роста погрешности при увеличении высоты расположения исследуемого уровня в облаке следует рассматривать предлагаемый способ в качестве консультативного и искать пути его совершенствования. Одно из направлений дальнейшей работы видится в применении других, более сложных моделей развития конвективного облака и разработке программных продуктов по реализации моделей конвекции [7].




 , м
, м