Постановка и решение задач региональной экологии для полных уравнений динамики атмосферных процессов и кинетических уравнений физико-химических превращений примесей в виде аэрозолей относится к числу сложных задач вычислительной математики и техники. Одной из главных задач, возникающих при реализации математических моделей основных задач региональной экологии, является снижение требований к вычислительным средствам по быстродействию и объему памяти. Усложняет задачу также нелинейность уравнений и негладкость их коэффициентов, что способствует поиску новых подходов в решении таких задач. Таким образом, цель настоящего исследования заключается в решении различных вопросов применения метода расщепления и спектральных вычислительных методов Галеркина к задачам (1) и (2) с учетом качественных особенностей этих задач.
В области 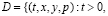
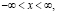
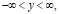
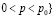 евклидова пространства в прямоугольной системе декартовых координат (t, x, y, p) рассмотрим задачу совместного расчета метеоэлементов атмосферы и характеристик региональной экологии в предположении, что термогидродинамические процессы среды описываются квазигеострофическими и гидростатическими уравнениями, а экологически вредные примеси представляют собой трехфазную смесь газа, жидкости и твердого вещества в виде частиц аэрозолей.
евклидова пространства в прямоугольной системе декартовых координат (t, x, y, p) рассмотрим задачу совместного расчета метеоэлементов атмосферы и характеристик региональной экологии в предположении, что термогидродинамические процессы среды описываются квазигеострофическими и гидростатическими уравнениями, а экологически вредные примеси представляют собой трехфазную смесь газа, жидкости и твердого вещества в виде частиц аэрозолей.
Тогда математическая постановка рассматриваемой задачи примет вид комплекса из двух задач:
1. Задача расчета метеоэлементов атмосферы региона в следующей постановке:
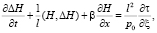 (1)
(1)
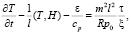
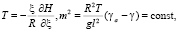
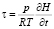 , p = p0, τ = 0, p = 0.
, p = p0, τ = 0, p = 0.
2. Задача переноса экологически вредных примесей в атмосфере региона в постановке вида
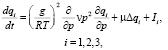 (2)
(2)
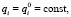 t = 0, qi = 0, p = 0, p = p0.
t = 0, qi = 0, p = 0, p = p0.
В формулировках задач (1) и (2) использованы следующие обозначения [1]: 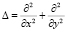 – оператор Лапласа, l – параметр Кориолиса для точек земной поверхности вдали от экватора, H = gz – новая неизвестная функция, g – ускорение силы тяжести, p – атмосферное давление,
– оператор Лапласа, l – параметр Кориолиса для точек земной поверхности вдали от экватора, H = gz – новая неизвестная функция, g – ускорение силы тяжести, p – атмосферное давление, 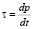 играет роль вертикальной составляющей вектора скорости, которая описывает смещение частицы воздуха относительно изобарических поверхностей, T – температура, γa – адиабатический градиент температуры, cp – удельная теплоемкость воздуха при постоянном давлении, ε – приток тепла к единице массы воздуха, который будем считать известным, R – универсальная постоянная, p0 – среднее давление на земной поверхности, принимаемое равным 1000 мб,
играет роль вертикальной составляющей вектора скорости, которая описывает смещение частицы воздуха относительно изобарических поверхностей, T – температура, γa – адиабатический градиент температуры, cp – удельная теплоемкость воздуха при постоянном давлении, ε – приток тепла к единице массы воздуха, который будем считать известным, R – универсальная постоянная, p0 – среднее давление на земной поверхности, принимаемое равным 1000 мб, 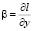 – коэффициент, учитывающий изменение параметра Кориолиса с широтой,
– коэффициент, учитывающий изменение параметра Кориолиса с широтой, 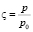 ,
, 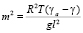 и изменяются по высоте незначительно, u, v – горизонтальные составляющие вектора скорости воздуха; ν, μ – коэффициенты турбулентной диффузии примесей; u, ν, τ – составляющие вектора скорости переноса примесей в атмосфере; Ii – мощности источников вредных примесей с учетом физико-химического взаимодействия примесей между собой и со средой. При определении функционального вида источников примесей учитываются выпадения тяжелых жидких и твердых вредных примесей на поверхности земли путем учета величины вертикальной скорости частиц под действием силы тяжести в уравнениях переноса аэрозолей.
и изменяются по высоте незначительно, u, v – горизонтальные составляющие вектора скорости воздуха; ν, μ – коэффициенты турбулентной диффузии примесей; u, ν, τ – составляющие вектора скорости переноса примесей в атмосфере; Ii – мощности источников вредных примесей с учетом физико-химического взаимодействия примесей между собой и со средой. При определении функционального вида источников примесей учитываются выпадения тяжелых жидких и твердых вредных примесей на поверхности земли путем учета величины вертикальной скорости частиц под действием силы тяжести в уравнениях переноса аэрозолей.
Заметим, что в настоящее время накоплен значительный материал по решению задачи (1) применительно к кратковременному прогнозу погоды. Для эффективного использования результатов численного решения задачи (1) для исследования экологических процессов региона и их анализа и прогноза на основе решения задачи (2) большое значение имеет применение вычислительных методов, понижающих требования к вычислительным средствам по быстродействию и объему памяти.
Об одной схеме расщепления системы уравнений динамики квазигеострофической и гидростатической атмосферы региональной экологии по физическим процессам
Основная краевая задача для системы уравнений динамики квазигеострофической и гидростатической атмосферы представляет собой сложную задачу математической физики для системы трех нелинейных уравнений в частных производных второго порядка (1). В результате решения указанной краевой задачи получим численное значение поля давления, температуры и вертикальной скорости как функции времени и пространственных координат, что связано с выполнением большого объема вычислительных работ.
Для упрощения задачи применен метод расщепления к системе уравнений краевой задачи (1) по физическим процессам. В результате несложных преобразований системы уравнений рассматриваемой задачи получим следующие три уравнения второго порядка для искомых величин:
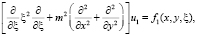 (3)
(3)
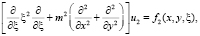 (4)
(4)
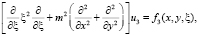 (5)
(5)
где 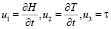 ,
,
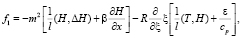
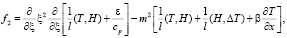 (6)
(6)
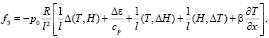
Уравнения (3)–(5) представляют собой эллиптические уравнения, вырождающиеся на границе области решения задач. Различные задачи математической физики для вырождающихся эллиптических уравнений встречаются при решении задач прикладного характера (например, в газовой динамике).
Общие математические вопросы корректной постановки различных задач математической физики для вырождающихся эллиптических уравнений подробно исследованы в ряде работ различными исследователями, такими как Ф. Трикоми, Е. Хольмгрен, С. Геллерстедт, Ф.И. Франкль, П. Жермен, Р. Бадер, А.В. Бицадзе, К.Е. Бабенко, М.В. Келдыш [2], С.А. Терсенов, Хоу Чунь-И, Ян Гуан-Цзинь, Чен Лян-цзинь, О.А. Олейник, С.Г. Михлин, М.И. Вишик, Л.Д. Кудрявцев, Г. Фикер, М.М. Смирнов [3] и др.
Аналогичные вопросы применительно к вырождающимся на границе области уравнениям динамики атмосферных процессов исследованы С.В. Немчиновым (известная в литературе схема Немчинова – Садокова – Робера [4]), которые служат хорошим математическим обоснованием постановок задач по динамике крупномасштабных атмосферных процессов.
Качественный анализ влияния стратификации на динамику атмосферных процессов региона
Основные уравнения динамики квазигеострофической и гидростатической атмосферы в форме (3)–(5) содержат параметр состояния стратификации атмосферы в виде
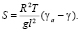
В зависимости от знака параметра стратификации атмосфера может находиться в трех состояниях:
1) 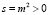 – устойчивое состояние;
– устойчивое состояние;
2) 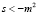 – неустойчивое состояние;
– неустойчивое состояние;
3) s = 0 – безразличное состояние.
Основные уравнения динамики атмосферы в виде уравнений (3)–(5), представляющих собой эллиптические уравнения и вырождающиеся по вертикальной координате на границе области решения задачи, получены в предположении, что параметр стратификации 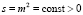 , т.е. атмосфера стратифицирована устойчиво.
, т.е. атмосфера стратифицирована устойчиво.
Рассмотрим случай, когда атмосфера стратифицирована неустойчиво, т.е. 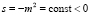 . Тогда уравнения (3)–(5) примут вид
. Тогда уравнения (3)–(5) примут вид
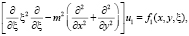 (7)
(7)
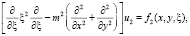 (8)
(8)
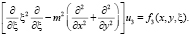 (9)
(9)
Уравнения (7)–(9) представляют собой гиперболические уравнения, вырождающиеся на границе области решения задачи. Эти уравнения качественно отличаются от эллиптических уравнений.
Для вырождающихся гиперболических уравнений исследованы задачи с начальными данными, когда заданные функции гладкие [3], такими учеными, как Г. Дарбу, Ф. Трикоми, С. Геллерстедт, Ф.И. Франкль, И.С. Березин, А.В. Бицадзе, К.И. Бабенко, М. Проттер, Г. Хельвиг, М.М. Смирнов, и другими.
В заключение параграфа рассмотрим случай, когда состояние стратификации атмосферы является безразличным, т.е. 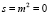 . Тогда уравнения (3)–(5) примут вид
. Тогда уравнения (3)–(5) примут вид
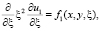 (10)
(10)
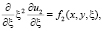 (11)
(11)
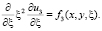 (12)
(12)
Уравнения (10)–(12) качественно отличаются от эллиптических и гиперболических уравнений, вырождающихся на границе области по вертикальной координате. Решение различных задач математической физики для этих уравнений находится значительно проще.
Основные эллиптические краевые задачи расчета метеоэлементов атмосферы региона
Задача A: Расчет динамических характеристик давления.
В области 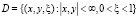 рассмотрим эллиптическое уравнение, вырождающееся на границе области решения задачи по вертикальной координате (3):
рассмотрим эллиптическое уравнение, вырождающееся на границе области решения задачи по вертикальной координате (3):
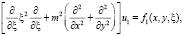 (13)
(13)
где 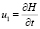 ,
, 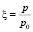 ,
, 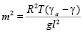 , р0 = 1000 мб – среднее давление на земной поверхности, f1(x, y, ξ) из (6).
, р0 = 1000 мб – среднее давление на земной поверхности, f1(x, y, ξ) из (6).
Дополним уравнение (13) граничными условиями [1]:
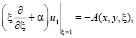
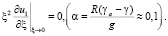 (14)
(14)
Таким образом, задача расчета динамических характеристик давления атмосферы свелась к краевой задаче (13), (14) для уравнения эллиптического типа.
Задача B: Расчет динамических характеристик температуры.
В рассматриваемой области D рассмотрим эллиптическое уравнение, вырождающееся на границе области решения задачи по вертикальной координате (4):
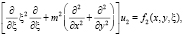 (15)
(15)
где 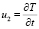 , f2(x, y, ξ) из (6).
, f2(x, y, ξ) из (6).
Дополнив уравнение (15) граничными условиями [1], получим
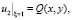
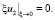 (16)
(16)
Следовательно, задача расчета динамических характеристик температуры в атмосфере свелась к краевой задаче (15), (16) для уравнения эллиптического типа.
Задача C: Определение вертикальной составляющей скорости в атмосфере.
В рассматриваемой области D рассмотрим эллиптическое уравнение, вырождающееся на границе области решения задачи по вертикальной координате (5):
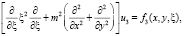 (17)
(17)
где u3 = τ, а вид функции f3(x, y, ξ) приведен в (6).
Уравнение (17) описывает вертикальные движения, связанные с крупномасштабной циркуляцией атмосферы. Вертикальные движения осуществляют перераспределение масс воздуха и энергии между различными уровнями атмосферы.
Как и выше, дополним уравнение (17) граничными условиями [1]:
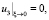
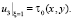 (18)
(18)
Таким образом, задача определения вертикальной составляющей скорости атмосферы свелась к краевой задаче (17), (18) для уравнения эллиптического типа.
Решение эллиптических краевых задач расчета давления, температуры и вертикальной скорости атмосферы спектральным методом Галеркина
Классический приближенный метод Галеркина используется как эффективный вычислительный метод для решения многих задач науки, техники и технологий.
Нахождение как аналитического, так и численного решения задач региональной экологии представляет сложную проблему в первую очередь ввиду нелинейности уравнений и негладкости их коэффициентов, поэтому актуальны новые подходы к решению таких задач. Этими же причинами обусловлено применение численных методов математической физики на основе метода Галеркина, показывающих хорошую эффективность при расчетах [5–8].
Вычислительные методы на основе метода Галеркина развиваются в двух направлениях. Первое направление – использование метода конечных элементов, то есть использование в качестве базисных функций метода Галеркина локальных полиномов невысокой степени. Второе направление – использование базисных функций, определенных в области решения рассматриваемой задачи на основе решения спектральных задач, связанных с решаемой задачей. Эти базисные функции являются глобальными и ортогональными для решаемой основной задачи.
К настоящему времени метод Галеркина с базисными функциями, построенными при решении вспомогательных спектральных задач, использовался для различных прикладных задач. Наиболее часто он применяется при решении двух классов проблем: глобальное атмосферное моделирование и фундаментальные исследования турбулентности.
В настоящей работе, имея в виду мезомасштабный анализ и прогноз атмосферных процессов региона применительно к анализу и прогнозу экологической обстановки региона, будем пользоваться методом Галеркина с базисной функцией, построенной на основе решения вспомогательных спектральных задач.
Чтобы получить представление о важнейших особенностях метода Галеркина, рассмотрим в компактной форме алгоритм решения краевой задачи для линейного дифференциального уравнения.
Пусть в области D(x, y) евклидова пространства с границей ∂D рассматривается краевая задача в операторной форме:
L(u) = 0, 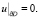 (19)
(19)
Для решения краевой задачи (19) методом Галеркина применяется следующий алгоритм [9]:
1. Построение базисных функций метода на основе решения спектральных задач.
2. Конструирование приближенного решения задачи в виде
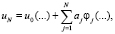
где функция u0 выбирается так, чтобы граничные условия удовлетворялись приближенно, а φj – собственные функции спектральных задач, aj – неизвестные коэффициенты, подлежащие определению.
3. Находим выражение для невязки R по формуле
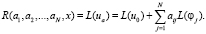
4. Предположим, что область D представляет гильбертово пространство со скалярным произведением
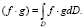
5. Для определения неизвестных коэффициентов aj решаем систему уравнений
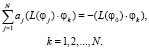 (20)
(20)
Подстановка значений коэффициентов в формулу для приближенного решения дает искомое решение uN рассматриваемой задачи (19).
Как следует из алгоритма, метод Галеркина сводит краевые задачи для уравнений в частных производных приближенно к задачам для системы обыкновенных дифференциальных уравнений или алгебраических уравнений, для которых можно использовать хорошо развитый численный метод. В случае неограниченных областей имеется возможность применять асимптотические методы решения таких уравнений. Программы для проведения вычислительных экспериментов получаются довольно простыми (стандартными) и не требуют большой затраты оперативной памяти машин.
Построение базисных функций метода Галеркина на основе решения вспомогательных спектральных задач
В области 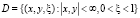 точек евклидова пространства с декартовыми координатами рассмотрим эллиптический оператор расщепленных уравнений динамики квазигеострофической и гидростатической атмосферы в виде
точек евклидова пространства с декартовыми координатами рассмотрим эллиптический оператор расщепленных уравнений динамики квазигеострофической и гидростатической атмосферы в виде
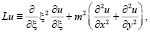
где 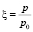 – приведенная высота.
– приведенная высота.
В цилиндрической системе координат (r, φ, ξ), связанных с прямоугольными координатами (x, y, ξ) соотношениями 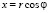
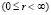 ,
, 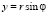
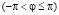 , ξ = ξ
, ξ = ξ 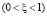 , оператор (5.1) приводится к виду
, оператор (5.1) приводится к виду
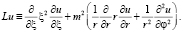 (21)
(21)
Рассмотрим краевую задачу для области, ограниченной двумя параллельными плоскостями применительно к задачам A, B, C.
Предположим, что искомая функция u1 и граничные условия задачи А (13) не зависят от φ.
Частные решения уравнения (21) ищем в виде
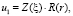
где множители представляют собой интегралы дифференциальных уравнений:
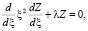 (22)
(22)
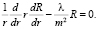 (23)
(23)
Найдем общее решение дифференциальных уравнений (22), (23).
Вспомогательную задачу рассмотрим для уравнения (22) в виде: найти общее решение уравнения (22) в области 0 < ξ < 1, удовлетворяющее граничным условиям:
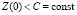 , Z(1) = 0. (24)
, Z(1) = 0. (24)
Как показано в [3], общее решение уравнения (22) имеет вид
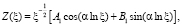 (25)
(25)
где 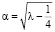 , A1, B1 – произвольные постоянные интегрирования.
, A1, B1 – произвольные постоянные интегрирования.
Краевое условие (24) показывает, что A1 = 0. Полагая несущественный в данном случае множитель B1 = 1, формулу (25) можно переписать в виде
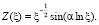 (26)
(26)
Заметим, что при 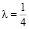
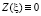 , а при
, а при 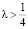 имеет место равенство [3]:
имеет место равенство [3]:
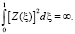
В обоих случаях Z(ξ) не является собственной функцией оператора вида
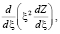 (27)
(27)
где 0 < ξ < 1.
Вместо функции (26) рассмотрим преобразованную функцию в виде 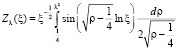 , или
, или 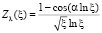 . Функция Zλ(ξ) при любом
. Функция Zλ(ξ) при любом 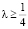 обладает следующими свойствами [3]:
обладает следующими свойствами [3]:
1) 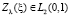 и является собственной функцией оператора (27);
и является собственной функцией оператора (27);
2) Zλ(ξ) обладает свойством полноты.
Теперь найдем общее решение дифференциального уравнения (23):
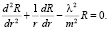 (28)
(28)
Пусть в уравнении (28) λ = nπi, где n = 1, 2, 3,..., i2 = –1. Тогда (28) перепишется в виде
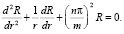 (29)
(29)
Общее решения уравнения (29) имеет вид
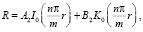
где 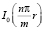 и
и 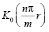 – цилиндрические функции мнимого аргумента, обладающие свойствами:
– цилиндрические функции мнимого аргумента, обладающие свойствами:
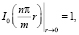
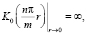
а A2 и B2 – произвольные постоянные интегрирования.
Для ограниченного решения задачи на оси цилиндра положим B2 = 0 и получим
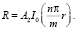
Следовательно, имеем следующую совокупность частных решений вспомогательной задачи:
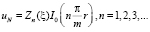
Таким образом, искомое решение однородного варианта рассматриваемой задачи A может быть построено путем суперпозиции частных решений в виде
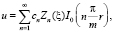
где cn – искомые коэффициенты.
Для определения коэффициентов cn, n = 1, 2, 3,… воспользуемся условием ортогональности невязки приближенного решения uN спектральными функциями Zn(ξ) 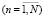 .
.
Получим систему уравнений для искомых коэффициентов в виде
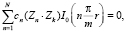
где k = 1, 2, 3,…,N, а (Zn•Zk) здесь символ скалярного произведения.
Подстановка значений коэффициентов 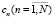 в формулу для приближенного решения uN дает искомое решение рассматриваемой задачи.
в формулу для приближенного решения uN дает искомое решение рассматриваемой задачи.
Методы решения неоднородных задач региональной экологии
Применение спектрального вычислительного метода Галеркина для решения первой краевой задачи для однородного эллиптического уравнения с вырождением по вертикальной координате, рассмотренной выше, базируется на использовании системы частных решений уравнений, полученных при помощи разделения переменных.
Рассмотрим класс задач региональной экологии, который описывается неоднородными уравнениями и неоднородными граничными условиями.
Для простоты дальнейших рассуждений рассмотрим постановку неоднородной задачи в операторной форме: уравнение
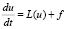 (30)
(30)
с граничными условиями
B(u) = 0. (31)
Решение задачи (30), (31), основанное на ортонормированных полных базисных функциях φi(x), введем в виде
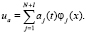
При этом N уравнений для коэффициентов aj примут вид:
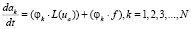 ,
,
а l уравнений получаются из граничных условий
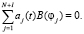 (32)
(32)
Приближенное решение ua, полученное для уравнения в [5, с. 243–244]
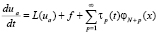
является точным.
Коэффициенты 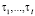 получаются из уравнения (32). Остальные коэффициенты τ соответствуют формулам
получаются из уравнения (32). Остальные коэффициенты τ соответствуют формулам
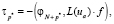
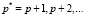
Таким образом, алгоритм решения задач региональной экологии с применением метода расщепления и спектрального метода Галеркина можно описать в следующем виде:
1. Математическая постановка задачи анализа и прогноза экологической ситуации в регионе.
2. Аналитическое расщепление задачи и анализ полученных расщепленных задач (позволяет упростить задачу, разбив ее на более простые, и требует меньшего объема вычислительных работ).
3. Анализ влияния стратификации на динамику атмосферных процессов решаемой задачи.
4. Применение к расщепленным задачам спектрального метода Галеркина (позволяет уменьшить объем вычислительных работ).
5. Расчет приближенного решения стандартными методами вычислительной математики (например, методом Рунге – Кутты).
Заключение
Полученные результаты позволяют видеть, что предложенный алгоритм является довольно эффективным способом получения приближенного решения задач анализа и прогноза экологической обстановки региона, представленных в виде системы уравнений термогидродинамики квазигеострофической и гидростатической атмосферы и системы уравнений переноса экологически вредных примесей в виде трехфазных аэрозолей. В особенности это касается случаев, когда требуется найти приближенное решение оперативно при ограниченных вычислительных возможностях и, вероятно, некорректных входных статистических данных региона.
Вопросы существования и сходимости приближенных решений, полученных методом Галеркина, подробно описаны в [10–12]. Для более подробного изучения других способов применения указанной модификации спектрального метода Галеркина можно рекомендовать работу [13]. Заметим, что если предложенные вычислительные методы или их модификации дают излишне сложные решения, то для решения региональных задач экологии целесообразно пользоваться методами Гринберга [14].



