Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Эволюция климата Земли на геологические сроки в значительной степени обусловлена вариациями суммарной солнечной радиации [1] и изменениями в содержании парниковых газов в атмосфере. Изменения климата влияют на растительность [2].

Расширение наземных растений вместе с океаном позволило обеспечить долговременную обитаемость на планете. Человечество использует ископаемые виды топлива, к середине XXI в. значения CО2 будет одинаковы с ранним эоценом (50 млн лет назад). Если концентрация CО2 продолжит расти и в XXIII в., земля будет реагировать как за полтора миллиарда лет [3].

Понимание реакции растений на факторы окружающей среды необходимо для прогнозирования изменений темпов поглощения углерода в лесах при различных условиях окружающей среды. В Финляндии имеется представление о реакции молодых лиственных деревьев на повышение температуры воздуха во взаимодействии с тропосферным озоном. Эти знания повышают шансы на разработку моделей для включения параметров, которые описывают лесную систему в изменяющихся климатических условиях [4]. Можно утверждать, что будущее сдерживания количества СО2 находится в увеличении площади лесов [5, 6].

Динамику температуры [7] можно описать множеством асимметричных вейвлетов (множеством квантов поведения) вплоть до ошибки измерений. Аналогично хорошо квантуется содержание СО2 в атмосфере. По вейвлетам универсальной конструкции изменяется динамика углерода в Европе [8].

Рост растений – сложный процесс, в его основе лежат такие фундаментальные явления, как ритмичность, полярность, дифференциация, раздражимость, корреляция. Эти процессы являются общими для онтогенеза живых организмов. Онтогенез – индивидуальное развитие организма от зиготы (или вегетативного зачатка) до природной смерти. Благодаря активной деятельности меристем и фотосинтетической активности листьев зеленое растение приобретает ряд черт, которые характеризуют его рост. В процессе онтогенеза растения рост наблюдается на протяжении основных этапов его жизненного цикла [9–11]. Поэтому в дальнейших исследованиях можно выявлять закономерности влияния метеорологических параметров на динамику вегетативных органов растений.

В экологических технологиях с использованием листьев березы повислой постепенно приходит понимание необходимости моделирования взаимных связей между параметрами структуры листьев растений методом идентификации [12]. Это изобретение относится к инженерной биологии и биоиндикации окружающей среды измерениями качества ростовых органов различных видов растений, преимущественно древесных растений, например проб в виде листьев берез без их срезания с простой и небольшой листовой пластинкой.

Цель статьи: повышение точности индикации качества окружающей листья березы локальной среды по патенту 2606189 на изобретение сбоку на высоте 1,5–2,0 м со стороны преобладающих ветров по динамике с 15 июля по 23 сентября 2018 г. средней ширины 10 учетных листьев около автомобильной дороги с интенсивным движением.

Материалы и методы исследования

В табл. 1 приведены средние ширины для 10 учетных листьев, принятых без срезания и измеренные с 27 июля по 23 сентября 2018 г. Всего получилось 18 строк. Первая точка 01 мая в 2018 г. оказалась началом вегетационного периода, поэтому ставим 0.

Колебания, в частности и тренды, записываются волновой формулой [12] вида

,

,

, (*)

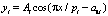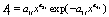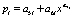где y – показатель (зависимый фактор), i – номер составляющей модели (*), m – количество членов в модели (*), x – объясняющая переменная (влияющий фактор), a1...a8 – параметры модели (*), принимающие числовые значения в ходе структурно-параметрической идентификации в программной среде CurveExpert-1.40, Ai – амплитуда (половина) вейвлета (ось y), pi – полупериод колебания (ось x).

Мы исключаем меру значимости 0,05 % [13] и оцениваем адекватность формул по коэффициенту корреляции. Все 10 статистических моделей получились с адекватностью выше 0,999. Поэтому динамика роста и спада листьев имеет высокую квантовую определенность.

Результаты исследования и их обсуждение

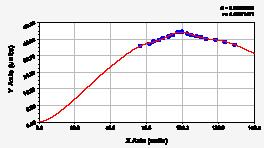
В табл. 2 приведены параметры модели (*) с двумя составляющими, первый из которых является трендом в виде биотехнического закона [12]. Цикличность колебания на 01.05.2018 г. в виде полупериода показывает параметр a5i. Полупериод колебания в начале вегетационного периода для 10 берез изменяется от 1,32 (ул. Панфилова) до 21,35 суток (ул. Лебедева).

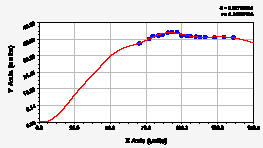
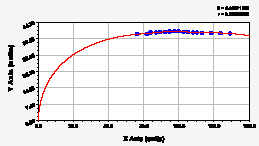
На рис. 1 и 2 приведены графики двухчленных формул по данным табл. 2. Все они одинаковы по конструкции, но имеют разный характер изменения во времени. Тогда можно утверждать, что динамика параметров листьев березы повислой в период вегетации около максимума приращения является очень высокоадекватной с коэффициентом корреляции более 0,999, то есть среднее поведение 10 учетных листьев имеет квантовую определенность. Но метеопараметры за период вегетации березы повислой имеют сильную квантовую запутанность. Тогда в дальнейшем необходимо понять, как же листья березы за 180 млн лет эволюции получили такую высокую колебательную адаптивность? Такое чувство, будто бы они понимают и ведут своими вегетативными органами осознанно к изменениям в окружающей группу учетных листьев среде.

Таблица 1

Средняя ширина 10 учетных листьев березы повислой для г. Йошкар-Ола

Примечание. Полужирным шрифтом показаны максимальные значения средней ширины.

Таблица 2

Модели (*) динамики средней ширины учетных листьев березы повислой

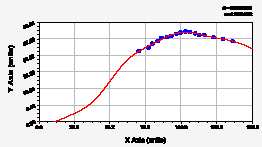
ул. Лебедева Воскресенский пр-т

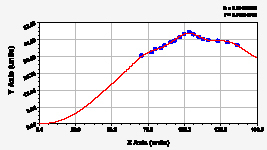
ул. Эшкинина пр. Ленина

Рис. 1. Графики динамики средней ширины группы из 10 учетных листьев березы повислой

Для оценки поведения групп листьев введем новый критерий – коэффициент динамичности, равный отношению разницы между фактом и трендом к факту средней ширины (табл. 3). Максимумы ширины листьев дали и наибольшие значения коэффициента динамичности.

Этот критерий позволяет ранжировать березы по убыванию влияния колебаний.

По табл. 3 места по ухудшению условий распределяются так: 1) 0,0072 – ул. Осипенко, на которой почти нет автомашин; 2) 0,0073 – ботанический сад, очень малое влияние забора вокруг объекта; 3) 0,0189 – ул. Панфилова; 4) 0,0198 – ул. Лебедева; 5) 0,0270 – проспект Ленина; 6) 0,0275 – ул. Строителей; 7) 0,0327 – проспект Карла Маркса; 8) 0,0438 – бульвар Чавайна; 9) 0,0431 – ул. Эшкинина; 10) 0,0487 – Воскресенский проспект.

Так что же лучше: спокойная жизнь при низком коэффициенте динамичности или же наибольшее приращение средней ширины учетных листьев березы повислой? По средней максимальной ширине листа из табл. 1 березы по ухудшению продуктивности расположились так: 1) 48,66 мм – Воскресенский проспект; 2) 45,92 мм – ул. Лебедева; 3) 44,71 мм – бульвар Чавайна; 4) 44,39 мм – ул. Карла Маркса; 5) 44,09 мм – ул. Осипенко; 6) 42,25 мм – ул. Строителей; 7) 40,71 мм – ботанический сад; 8) 40,11 мм – проспект Ленина; 9) 39,77 мм – ул. Эшкинина; 10) 39,56 мм – ул. Панфилова. Конечно же, на скорость приращения и достижение средней максимальной ширины учетных листьев влияет и собственное физиологическое состояние дерева. Например, береза с продуктивными листьями по табл. 1 за четверо суток с 15,08 по 19,08 изменила на Воскресенском проспекте среднюю ширину листьев с 47,87 до 48,66 мм или имела скорость приращения (48,66 – 47,87) / 4 = = 0,198 мм. А на ул. Панфилова средняя скорость роста ширины листьев равна (39,56 – 39,10) / 4 = 0,115 мм.

Таблица 3

Коэффициент динамичности роста листьев березы повислой

Примечание. Полужирным шрифтом показаны максимальные значения коэффициента динамичности.

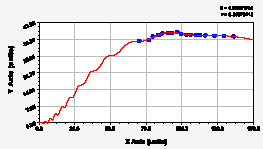
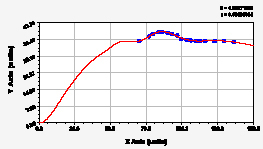
б-р Чавайна ул. Панфилова

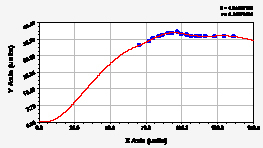
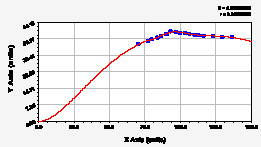
ул. Карла Маркса ул. Строителей

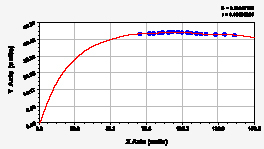
Ботанический сад ул. Осипенко

Рис. 2. Графики динамики средней ширины группы из 10 учетных листьев березы повислой

Как известно, мониторинг окружающей среды выполняют по множеству видов загрязнений, содержание которых в воздухе, воде и почве не должно превышать предельно допустимых концентраций. Однако косвенный мониторинг через поведение учетных листьев березы повислой, в вегетационный период позволяет без измерения концентраций загрязнений провести экологическую оценку территории места произрастания данной березы. В итоге листья березы реагируют на все изменения в окружающей березу среде, причем учитывают и те воздействия, которые еще неизвестны человеку. В этом проявляется сущность наших способов индикации окружающей среды, и патент 2606189 становится пионерным решением.

Для принятия за критерии экологической оценки скорости приращения необходимо учитывать еще и физиологические параметры дерева, например классы санитарного состояния, возраст и другое. Таким образом, для индикации среды вокруг березы пока рекомендуется коэффициент динамичности при максимуме средних размеров учетных листьев.

Заключение

По патенту 2606189 на изобретение сбоку на высоте 1,5–2,0 м со стороны преобладающих ветров по динамике с 15 июля по 23 сентября 2018 г. измерялись средняя ширина 10 учетных листьев около автомобильной дороги. Параметры модели с двумя составляющими показали, что полупериод колебания в начале вегетационного периода для 10 берез изменяется от 1,32 до 21,35 суток. Все модели динамики одинаковы по конструкции, но имеют разный характер. Время вегетации около максимума роста влияет с коэффициентом корреляции более 0.999, поэтому поведение 10 листьев имеет квантовую определенность.

Для оценки поведения групп листьев введен новый критерий – коэффициент динамичности, равный отношению разницы между фактом и трендом к факту средней ширины. Максимумы ширины листьев дали и наибольшие значения коэффициента динамичности. Этот критерий позволяет ранжировать березы по убыванию влияния колебаний от влияния среды.

Средняя ширина 10 учетных листьев березы повислой показала очень малую погрешность, поэтому количество учетных листьев с одной локальной зоны можно уменьшить до 5. Измерение ширины учетных листьев до достижения максимума роста почти в два раза сокращает промежуток времени для проведения экспериментов. Это позволяет увеличить количество учетных деревьев, произрастающих в разных экологических условиях, а также уменьшить, например до двух суток, промежутки между измерениями. Время измерений в каждый год можно начать с 01 июля и продолжать до 20 августа.