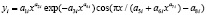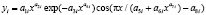Математико-геоморфологическое моделирование эрозионных ландшафтов с применением геоинформационной среды и космических снимков высокого разрешения дает возможность выявить основные характеристики ландшафтов в режиме реального времени и использовать их как основу для теоретических и экспериментальных исследований эколого-геоморфологических процессов. Таким образом, мы получаем современный инструмент изучения процессов, определяющих состояние и степень развития ландшафтов [1].
Продольный профиль руслового потока всегда имеет серии ступеней или, вернее, пологих волнообразных изгибов, не вызывающих разрыва непрерывности подобно порогам и водопадам. Ступенчатость как обязательная особенность русловых потоков отмечалась большинством исследователей [2]. Но волновых уравнений до сих пор не было получено.
Цель – анализ асимметричных вейвлетов распределений высоты от истока до устья по 290 характерным точкам и влияния широты и долготы малой реки Ировка.
Материалы и методы исследования
По космическим снимкам были измерены координаты (широта, долгота, высота) по рекомендациям [3].
На линии стрежня малой реки выбираются характерные точки от истока до устья по резким изменениям продольного профиля малой реки, например, при повороте русла в любую сторону в плане более 10–150. По результатам измерений составляется таблица данных для моделирования методом идентификации устойчивых закономерностей [4].
В табл. 1 даны измерения координат и их сравнение с моделями: ε12 – остатки после 12-й составляющей (1); Δ – относительная погрешность.
Таблица 1
Ранговые распределения высоты характерных точек русла р. Ировка
|
Ранг точки |
Ранг Rh |
Широта α, минута |
Долгота β, минута |
Высота h, м |
Расчетные значения от ранга |
||
|
h, м |
ε12, м |
Δ, % |
|||||
|
0 |
0 |
0 |
17.39 |
59 |
59.1 |
0.123212 |
0.21 |
|
1 |
1 |
0.02 |
17.50 |
52 |
52.0 |
–0.0367244 |
–0.07 |
|
2 |
3 |
0.19 |
17.62 |
48 |
48.0 |
0.0170352 |
0.04 |
|
3 |
3 |
0.2 |
17.67 |
48 |
48.0 |
0.0170352 |
0.04 |
|
4 |
3 |
0.27 |
17.64 |
48 |
48.0 |
0.0170352 |
0.04 |
|
5 |
6 |
0.55 |
17.95 |
47 |
47.0 |
–0.0354557 |
–0.08 |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
286 |
247 |
23.83 |
1.970 |
4 |
4.0 |
–0.00580508 |
–0.15 |
|
287 |
247 |
23.84 |
2.019 |
4 |
4.0 |
–0.00580508 |
–0.15 |
|
288 |
269 |
23.87 |
2.035 |
2 |
2.1 |
0.0747201 |
3.74 |
|
289 |
286 |
23.89 |
2.017 |
0 |
–0.4 |
–0.422514 |
–∞ |
Гипсометрическая характеристика – одно из важнейших свойств рельефа. По степени приподнятости поверхности суши над уровнем океана выделяют низменный (абсолютная высота от 0 до 200 м) рельеф [5, с. 24–25]. Река Ировка относится к низменному уровню, в устье высота равна 89 м, а в истоке высота достигает 148 м над уровнем Балтийского моря [6].
Колебания (вейвлет-сигналы) записываются волновой формулой [4] вида
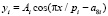 ,
,
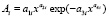 ,
,
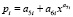 , (1)
, (1)
где y – показатель (зависимый фактор), i – номер составляющей модели (1), m – количество членов в общей модели (1), x – объясняющая переменная (влияющий фактор), a1...a8 – параметры модели (1), принимающие различные числовые значения в процессе структурно-параметрической идентификации в программной среде CurveExpert-1.40, Ai – амплитуда (половина) вейвлета (ось y), pi – полупериод колебания (ось x).
Результаты исследования и их обсуждение
На рис. 1 приведена пространственная гипсометрическая кривая по 290 характерным точкам изменения местной высоты от устья до истока реки в зависимости от местной широты и долготы.
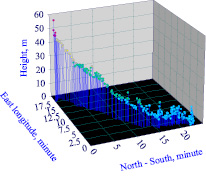
Рис. 1. Пространственная гипсометрия реки Ировка по влиянию местной широты и долготы на высоту
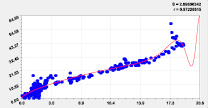
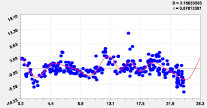
Влияние местной долготы Дополнительно влияние местной широты
Рис. 2. Влияние долготы и широты от истока до устья на высоту русла р. Ировка
Модель h = f(β, α) получена исходя из условия, что вначале выявляют однофакторные модели, а затем их расставляют по повышению коэффициента корреляции как меры адекватности выявленных закономерностей.
В табл. 2 приведены значения параметров (1) по двум членам влияния местной долготы на высоту, а в остатки от второго члена как влияющей переменной поставлены значения местной широты из данных табл. 1. На рис. 2 даны графики двух факторов.
Таблица 2
Влияние долготы и широты от истока до устья на высоту р. Ировка
|
Фактор и номер i |
Вейвлет |
Коэф. кор. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
β1 |
4.58566 |
0.73085 |
0 |
0 |
0 |
0 |
0 |
0 |
0.9723 |
|
β2 |
2.03445 |
0 |
–1.75365e–5 |
3.90439 |
42.76414 |
1.60613 |
1.03524 |
–1.26285 |
|
|
α1 |
2.30115 |
0 |
–0.026287 |
1 |
2.86126 |
0.019765 |
1 |
0.007428 |
0.6761 |
|
α2 |
5.55135e–130 |
165.9377 |
10.02393 |
1 |
0.039078 |
0.019846 |
1 |
2.21030 |
|
|
α3 |
1.54657 |
0 |
0 |
0 |
2.28105 |
0.0017154 |
1 |
–0.77225 |
|
Малая река Ировка по гипсометрической картине на рис. 1 протекает в прямоугольнике 23.89 минут длиной (по местной широте Север-Юг) и 18.89 минут шириной (по местной долготе). Резкие изменения кривизны русла в плане по 290 характерным точкам дали волновые уравнения по данным табл. 2. Первое уравнение влияния долготы показывает, что по мере возрастания восточной долготы происходит увеличение высоты реки по показательному закону. Из картины на рис. 1 видно, что увеличение высоты происходит от меньшей долготы (ближе к устью) до наибольшей долготы (ближе к истоку). При этом второе волновое уравнение показывает, что амплитуда возрастает по экспоненциальному закону роста, а полупериод колебания возрастает от 42.76 ранга при минимальной долготе.
Дополнительно влияние широты на высоту по третьему члену происходит по закону экспоненциального роста от истока до устья. Поэтому спад высоты происходит в основном из-за уменьшения местной долготы. Это зависит от восточного склона Вятского увала.
Этот третий член из табл. 2 является законом Лапласа (в математике), Мандельброта (в физике), Ципфа – Перла (в биологии) и Парето (в эконометрике). У закона a4i = 1.
После идентификации общей модели (1) было получено 12 вейвлетов рангового распределения местной высоты (табл. 3, рис. 3–5).
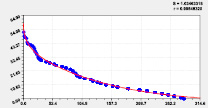
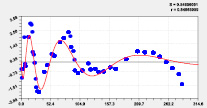
Двухчленный тренд Колебание
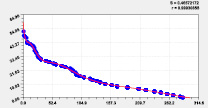
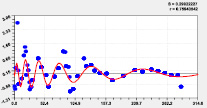
Двухчленный тренд и колебание Четвертая составляющая
Рис. 3. Графики тренда и двух колебаний рангового распределения высоты р. Ировка
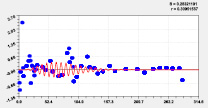
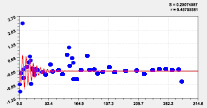
Пятая составляющая Шестая составляющая
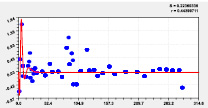
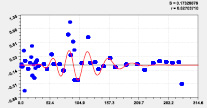
Седьмая составляющая Восьмая составляющая
Рис. 4. Графики моделей рангового распределения высоты р. Ировка
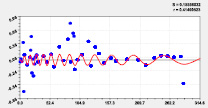
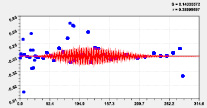
Девятая составляющая Десятая составляющая
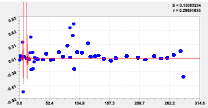
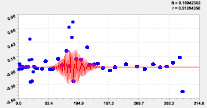
Одиннадцатая составляющая Двенадцатая составляющая
Рис. 5. Графики последних моделей рангового распределения высоты р. Ировка
Таблица 3
Параметры вейвлетов рангового распределения местной высоты р. Ировка
|
Номер i |
Вейвлет |
Коэф. кор. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
58.87679 |
0 |
0.00088082 |
1.09926 |
0 |
0 |
0 |
0 |
0.9993 |
|
2 |
–6.38434 |
0.48652 |
0.070117 |
0.46505 |
0 |
0 |
0 |
0 |
|
|
3 |
3.47327 |
0.84367 |
1.36494 |
0.26690 |
4.78474 |
0.51777 |
0.78599 |
5.06935 |
|
|
4 |
0.458135 |
0.692074 |
0.459628 |
0.418576 |
5.06960 |
0.168685 |
0.838476 |
8.53040 |
0.7594 |
|
5 |
9.3361e-7 |
4.10453 |
0.0650157 |
1 |
3.73444 |
0.0408429 |
0.489883 |
0.194488 |
0.3095 |
|
6 |
0.394701 |
1.23562 |
0.447487 |
0.682474 |
3.12365 |
0.551263 |
0 |
0 |
0.4576 |
|
7 |
0.781908 |
1.36008 |
0.256209 |
1.03850 |
3.16303 |
0.0119643 |
2.26069 |
2.1713 |
0.4440 |
|
8 |
3.18333e-11 |
6.49697 |
0.0664222 |
1 |
10.78055 |
0.0254631 |
0.996656 |
1.18507 |
0.6270 |
|
9 |
6726.89934 |
2.21488 |
14.79868 |
0.0997817 |
4.67037 |
0.00824933 |
1.19103 |
–1.11802 |
0.4141 |
|
10 |
5.0896e-9 |
4.247939 |
0.00189252 |
1.53230 |
1.47780 |
0 |
0 |
0.257972 |
0.3900 |
|
11 |
5.2799e-12 |
21.44634 |
2.22290 |
1 |
0.832376 |
0 |
0 |
3.50578 |
0.2969 |
|
12 |
3.27713e-47 |
2941689 |
0.214460 |
1.07043 |
1.05525 |
0 |
0 |
2.34453 |
0.5136 |
Первые три вейвлета дали по возможностям программной среды CurveExpert-1.40 коэффициент корреляции 0,9993. Первый член есть модифицированный нами закон Лапласа или Мандельброта [4] при условии a4i ≠ 1, и он показывает экспоненциальное снижение средней высоты двух берегов от истока до устья. Второй член показывает снижение высоты по биотехническому закону [4] примерно к середине длины реки. Приближенно два первых члена образуют тренд изменения линии водной поверхности малой реки (рис. 3). Остальные 10 волн (рис. 4 и рис. 5) показывают из-за положительного знака, колебательную адаптацию рельефа к возрастанию высоты. Первые два колебания показывают успокоение рельефа от истока.
Остальные восемь членов показывают локальное изменение высоты рельефа реки. Таким образом, высота вдоль малой реки изменяется, как широта и долгота, волнообразно, на что, конечно же, влияют колеблющиеся расстояния в плане и по высоте между характерными точками вдоль стрежня малой реки Ировка.
На рис. 4 и 5 заметны несколько коротких по характерным точкам вейвлетов. При этом члены № 6, 7 и 11 показывают сильную флюктуацию рельефа на верховье малой реки. При спаде уровня водности около истока летом ныне происходит пересыхание русла.
Дальнейшая идентификация модели (1) затрудняется, поэтому процесс выявления закономерностей останавливаем. Остатки меньше погрешности измерений ±0,5 м.
Четыре точки (с рангами 252, 263, 266 и 289) из-за h = 0 дали бесконечную погрешность. По интервалам 0.1 погрешность распределилась так (по модулю): при нуле 9 шт. (3,10 %); 0–0,1 % 46 шт. (15,86 %); 0,1–0,2 % 59 шт. (20,34 %); 0,2–0,3 % 11 шт. (3,79 %); 0,3–0,4 % 29 шт. (10 %); 0,4–0,5 % 7 шт. (2,41 %) и т.д. По крупным интервалам: 0–1,0 % всего точек 203 шт. (70 %); от 0 до 5 % 277 точек, что равно 95,52 % от 290 характерных точек. Норму погрешности измерений и моделирования примем 5 %, тогда оставшиеся 290 – 277 = 13 точек продольного профиля русла требуют отдельного рассмотрения.
На рис. 6 приведен график распределения погрешности модели по формуле
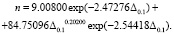 (2)
(2)
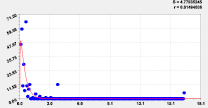
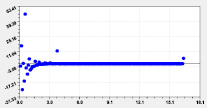
Двухчленный тренд погрешности Остатки после тренда
Рис. 6. Графики распределения погрешности моделирования высоты р. Ировка
Первый член (2) является законом Лапласа экспоненциального спада, а второе уравнение показывает стрессовое возбуждение [4] количества погрешностей. Сравнение показало, что модель (1) для широты получила 25 членов, для долготы 18 и для высоты 12 членов.
Таблица 4
Динамика S, м
|
Ранг вейвлета i |
Ст. отклонение S |
|
0 |
12,219 |
|
1 |
1,489 |
|
2 |
1,035 |
|
3 |
0,466 |
|
4 |
0,299 |
|
5 |
0,283 |
|
6 |
0,251 |
|
7 |
0,224 |
|
8 |
0,173 |
|
9 |
0,156 |
|
10 |
0,140 |
|
11 |
0,131 |
|
12 |
0,109 |
В правом верхнем углу графиков на рисунках приведены значения среднего квадратичного отклонения (стандартного отклонения) S. В табл. 4 даны ранги вейвлетов и расчетные значения фактического распределения стандартного отклонения.
Нулевой ранг получает уравнение y = a среднего арифметического значения. Первый ранг имеет первый член по табл. 3. Стандартное отклонение снижается от 12,219 для среднеарифметического уравнения до 1,489, то есть в 8,2 раза. После 12-го вейвлета трехкратное отклонение образует 0,3 м, что намного меньше фактической погрешности измерений ±0,5 м.
После идентификации (1) получена формула
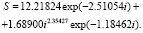 (3)
(3)
Первый член является снова законом Мандельброта и поэтому показывает некратное фрактальное распределение всех 12 вейвлетов.
Из остатков на рисунке видно, что третьим членом к формуле (3) станет асимметричный вейвлет. Это доказывает, что квантование высоты рельефа по фракталам может иметь не только некратное значение, но даже происходит по волновым уравнениям.
Заключение
Моделирование распределений приведенной к малой реке высоты позволило получить 12 вейвлетов с распределением 95,52 % точек при погрешности моделирования до 5 %. Первый член формулы распределения погрешностей в 290 точках русла реки является законом Лапласа экспоненциального спада, а второе уравнение показывает стрессовое возбуждение [4] количества погрешностей. Сравнение показало, что модель (1) для широты получила 25 членов, для долготы 18 и для высоты 12 членов.
Первые три члена модели высоты дали коэффициент корреляции 0,9993, уровень адекватности более 0,9 или сильнейшей связи. Остальные 9 члена повышают уровень адекватности почти до 1. В итоге высота как фактор проявляет определенность в квантовании.
Нулевой ранг при фрактальном распределении получает уравнение y = a среднего арифметического значения. Стандартное отклонение снижается от 12,219 для среднеарифметического уравнения до 1,489, то есть в 8,2 раза. После 12-го вейвлета трехкратное отклонение (правило три-сигмы) образует 0,3 м, что намного меньше фактической погрешности измерений ±0,5 м для высоты по космическим снимкам.