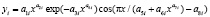Малые реки – наиболее уязвимое звено в речных системах, что связано с их небольшой водностью и невысокой эрозионно-транспортирующей способностью. Этим объясняется особая чувствительность русел малых рек к антропогенным воздействиям: строительству земляных плотин, мостов, обустройству бродов, местному водозабору и сливу неочищенных (как правило, сточных) вод, вырубке лесов и распашке водосборов [1]. При этом фрактальные распределения рек по длинам в речной сети имеют определенные преимущества [2].
Нами по космическим снимкам были измерены координаты (широта, долгота, высота) [3] по методическим рекомендациям [4]. По измерениям составлена таблица координат для идентификации закономерностей [5].
Цель исследования: анализ асимметричных вейвлетов у бинарных отношений между тремя координатами по 290 характерным точкам от истока до устья малой реки Ировка.
Материалы и методы исследования
В табл. 1 даны результаты измерения трех координат.
Таблица 1
Координаты характерных точек русла малой реки Ировка
|
Ранг точки |
Широта α, минута |
Долгота β, минута |
Высота h, м |
|
0 |
0 |
17.39 |
59 |
|
1 |
0.02 |
17.50 |
52 |
|
2 |
0.19 |
17.62 |
48 |
|
… |
… |
… |
… |
|
287 |
23.84 |
2.019 |
4 |
|
288 |
23.87 |
2.035 |
2 |
|
289 |
23.89 |
2.017 |
0 |
Гипсометрическая характеристика – одно из важнейших свойств рельефа. По приподнятости поверхности суши над уровнем океана выделяют низменный (абсолютная высота от 0 до 200 м) рельеф [6, с. 24–25]. Река Ировка имеет в устье высоту 89 м, а в истоке – 148 м (рис. 1).
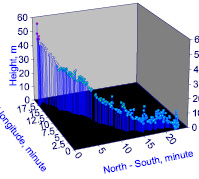
Рис. 1. Пространственная гипсометрия реки
Ировка по гипсометрической картине на рис. 1 протекает внутри прямоугольника 23.89 минут длиной (по местной широте) и 18.89 минут шириной (по местной долготе). Резкие изменения кривизны русла в плане по 290 характерным точкам дали несколько волновых уравнений.
Далее рассмотрим бинарные отношения.
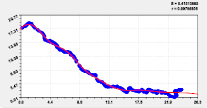
Колебания (вейвлет-сигналы) записываются волновой формулой [5] вида
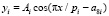 ,
,
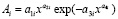 ,
,
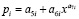 , (1)
, (1)
где y – показатель (зависимый фактор), i – номер составляющей модели (1), m – количество членов в (1), x – объясняющая переменная (влияющий фактор), a1...a8 – параметры (1), принимающие значения при структурно-параметрической идентификации в CurveExpert-1.40, Ai – амплитуда (половина) вейвлета (ось y), pi – полупериод колебания (ось x).
Результаты исследования и их обсуждение
После идентификации общей модели (1) из трех координат в табл. 2 были получены шесть бинарных отношений.
Таблица 2
Параметры моделей бинарных отношений координат реки Ировка
|
Номер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
Влияние высоты от устья до истока реки на долготу характерных точек русла |
|||||||||
|
1 |
0.036510 |
1.84872 |
0.00015250 |
2.25378 |
0 |
0 |
0 |
0 |
0,9967 |
|
2 |
2.17901 |
0 |
0.060421 |
0.28602 |
10.34394 |
–0.0034879 |
1.50771 |
1.02204 |
|
|
Влияние высоты от устья до истока реки на широту Север-Юг от истока до устья |
|||||||||
|
1 |
24.11765 |
0 |
0.021872 |
1.28116 |
0 |
0 |
0 |
0 |
0,9693 |
|
2 |
–4.11571e-20 |
33.78062 |
3.19877 |
1 |
10.11218 |
–0.14566 |
1.41996 |
–3.87447 |
|
|
Влияние долготы от левой точки русла на высоту от устья реки Ировка |
|||||||||
|
1 |
4.58566 |
0.73085 |
0 |
0 |
0 |
0 |
0 |
0 |
0,9723 |
|
2 |
2.03445 |
0 |
–1.75365e-5 |
3.90439 |
42.76414 |
–1.60613 |
1/03524 |
–1.26285 |
|
|
Влияние долготы от левой точки русла на широту Север-Юг от истока до устья |
|||||||||
|
1 |
22.87329 |
0 |
0;0022749 |
2.42253 |
0 |
0 |
0 |
0 |
0,9724 |
|
2 |
-9.48597 |
3.81920 |
2.13995 |
0.64925 |
0 |
0 |
0 |
0 |
|
|
3 |
3.10268e8 |
6.37127 |
19.73370 |
0.25275 |
0.41871 |
0.019294 |
1.94415 |
0.14850 |
|
|
Влияние широты Север-Юг от истока до устья на высоту от устья до истока реки |
|||||||||
|
1 |
58.96563 |
0 |
0.11761 |
0.85812 |
0 |
0 |
0 |
0 |
0,9859 |
|
2 |
–1.71136e6 |
0.70048 |
12.14870 |
0.057545 |
0 |
0 |
0 |
0 |
|
|
3 |
1.46900e-34 |
38.87949 |
1.67667 |
1.03588 |
83.45225 |
–4.18801 |
0.91671 |
–2.73588 |
|
|
Влияние широты Север-Юг от истока до устья на долготу от левой точки русла реки |
|||||||||
|
1 |
19.08116 |
0 |
0.039811 |
1.32388 |
0 |
0 |
0 |
0 |
0,9976 |
|
2 |
–1.61185e-6 |
26.25390 |
14.89933 |
0.49461 |
0 |
0 |
0 |
0 |
|
|
3 |
–2.09089 |
0 |
0.82090 |
0.40884 |
2.36913 |
0.0028086 |
1.55183 |
–0.35993 |
|
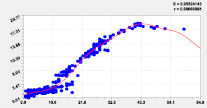
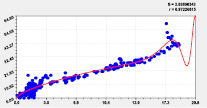
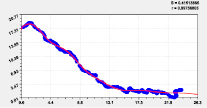
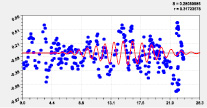
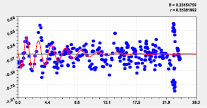
Наибольшую адекватность с коэффициентом корреляции 0,9976 получило влияние широты на долготу. На втором месте с корреляцией з.9967 оказалось влияние высоты точек русла малой реки на местную долготу, и оно в основном определяется рельефом Вятского увала. На третьем месте оказалось влияние широты на высоту с коэффициентом корреляции 0,9859.
И на последнем, шестом, месте находится обратное влияние высоты на местную широту в направлении Север-Юг. Все двух- и трехчленные модели имеют сильнейшую адекватность, то есть коэффициент корреляции составляет более 0,95.
Влияние высоты от устья до истока реки и долготы от левой точки русла
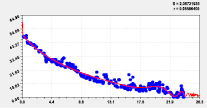
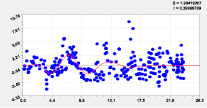
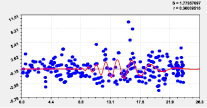
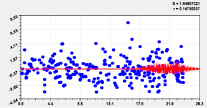
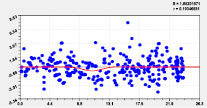
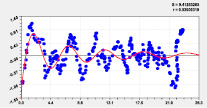
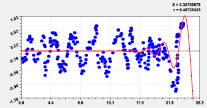
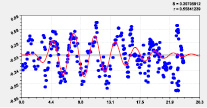
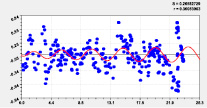
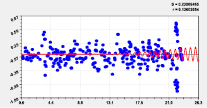
На рис. 2 и 3 приведены графики влияния высоты и долготы по моделям из табл. 2.
|
|
|
|
Тренд и колебание влияния на долготу |
Тренд и колебание влияния на высоту |
|
|
|
|
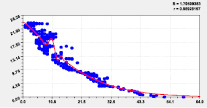
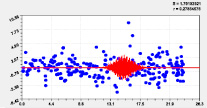
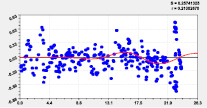
Тренд и колебание влияния на широту Рис. 2. Графики влияния высоты реки |
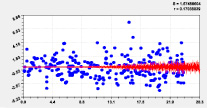
Тренд и колебание влияния на широту Рис. 3. Графики влияния долготы русла |
Высокая адекватность позволяет сделать вывод о том, что координаты русла малой реки обладают общими свойствами. Одним из них является непрерывность водного потока.
Влияние широты Север-Юг от истока до устья
Широта влияет на два остальных параметра (высоту и долготу) фрактально (табл. 3 включает 11 членов, табл. 4 – 13 вейвлетов). Причем эта фрактальность определяется некратной структурой составляющих (1).
Таблица 3
Влияние широты Север-Юг от истока до устья на высоту реки Ировка
|
Номер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
58.96563 |
0 |
0.11761 |
0.85812 |
0 |
0 |
0 |
0 |
0,9859 |
|
2 |
–1.71136e6 |
0.70048 |
12.14870 |
0.057545 |
0 |
0 |
0 |
0 |
|
|
3 |
1.46900e-34 |
38.87949 |
1.67667 |
1.03588 |
83.45225 |
–4.18801 |
0.91671 |
–2.73588 |
|
|
4 |
0.156044 |
3.10878 |
0.486002 |
1 |
2.82186 |
1.20712e-4 |
2.76209 |
1.22940 |
0,3909 |
|
5 |
2.89862e-15 |
20.01880 |
1.28894 |
1.01392 |
0.0715423 |
0.00979152 |
1.07050 |
13.45603 |
0,3601 |
|
6 |
5.09823e-99 |
116.00022 |
2.35448 |
1.33230 |
0.0777732 |
0 |
0 |
4.71515 |
0,2785 |
|
7 |
5.26586e-6 |
4.85253 |
0.153153 |
0.990526 |
0.106066 |
0 |
0 |
1.39946 |
0,1704 |
|
8 |
2.71862e-81 |
0 |
4.18864 |
1 |
0.113739 |
2.66500 |
0 |
0 |
0,1474 |
|
9 |
5.20858e-23 |
35.73529 |
3.03928 |
1.01566 |
4.04816 |
0.0655608 |
1.23614 |
–3.85008 |
0,1035 |
|
10 |
0.0921386 |
1.56575 |
0.172271 |
1 |
0.524478 |
4.53850 |
0 |
0 |
0,1791 |
|
11 |
0.896703 |
2.36906 |
0.877726 |
0.901428 |
0.771798 |
0 |
0 |
2.92625 |
0,1891 |
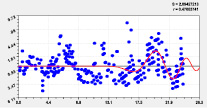
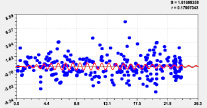
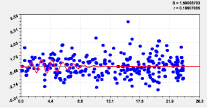
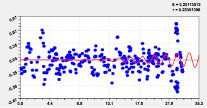
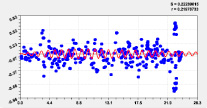
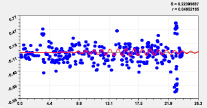
Адекватность влияния широты может достичь коэффициента корреляции 1. И этот факт показывает, что влияние местной широты обладает высокой определенностью квантования волновыми уравнениями (рис. 4–7). Это называется полным факторным анализом.
|
|
|
|
Двухчленный тренд и колебание |
Третья составляющая |
|
|
|
|
Четвертая составляющая |
Пятая составляющая |
|
|
|
|
Шестая составляющая |
Седьмая составляющая |
Рис. 4. Графики влияния широты Север-Юг от истока до устья на высоту реки Ировка
|
|
|
|
Восьмая составляющая |
Девятая составляющая |
|
|
|
|
10-ая составляющая |
11-ая составляющая |
Рис. 5. Графики влияния широты Север-Юг на высоту от устья до истока реки Ировка
|
|
|
|
Двухчленный тренд и колебание |
Третья составляющая |
|
|
|
|
Четвертая составляющая |
Пятая составляющая |
|
|
|
|
Шестая составляющая |
Седьмая составляющая |
Рис. 6. Графики влияния широты Север-Юг на долготу от левой точки русла реки Ировка
|
|
|
|
Восьмая составляющая |
Девятая составляющая |
|
|
|
|
10-ая составляющая |
11-ая составляющая |
|
|
|
|
12-ая составляющая |
13-ая составляющая |
Рис. 7. Графики влияния широты Север-Юг на долготу от левой точки русла реки Ировка
Таблица 4
Влияние широты Север-Юг от истока до устья на долготу реки Ировка
|
Номер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
19.08116 |
0 |
0.039811 |
1.32388 |
0 |
0 |
0 |
0 |
0,9976 |
|
2 |
–1.61185e-6 |
26.25390 |
14.89933 |
0.49461 |
0 |
0 |
0 |
0 |
|
|
3 |
–2.09089 |
0 |
0.82090 |
0.40884 |
2.36913 |
0.0028086 |
1.55183 |
–0.35993 |
|
|
4 |
1.95823e-5 |
0 |
0.448432 |
1.00282 |
0.0820466 |
0.0119878 |
1.00090 |
5.45636 |
0,4873 |
|
5 |
0.0168527 |
3.08551 |
0.378919 |
1.00055 |
1.58592 |
6.89209e-5 |
2.25901 |
2.74470 |
0,5584 |
|
6 |
4.51507e-6 |
4.65846 |
0.00126702 |
2.65421 |
0.156256 |
0.232502 |
0.219714 |
12.08418 |
0,3172 |
|
7 |
0.00742864 |
0 |
2.07429 |
0.127857 |
–0.0334208 |
1.99360 |
0.079573 |
6.22674 |
0,3006 |
|
8 |
1.14486e-8 |
7.88750 |
0.253085 |
1.12234 |
5.64354 |
1.01837 |
0 |
0 |
0,2100 |
|
9 |
1.59713e-7 |
5.97718 |
0.379652 |
0.825954 |
0.857850 |
0 |
0 |
6.11295 |
0,2035 |
|
10 |
1.28249 |
0.788528 |
1.19686 |
0.595343 |
0.772734 |
0.0263791 |
0.913011 |
1.77834 |
0,3538 |
|
11 |
1.79254e-13 |
11.76514 |
0.564683 |
0.905328 |
0.375291 |
0 |
0 |
2.47176 |
0,1360 |
|
12 |
0.0264789 |
1.10650 |
0.119784 |
0 |
0.497133 |
0 |
0 |
1.05946 |
0,2198 |
|
13 |
1.31795e-8 |
11.27609 |
2.044278 |
0.735657 |
0.594690 |
0 |
0 |
0.978506 |
0,0465 |
Таким образом, из трех координат для 290 характерных точек русла малой реки Ировка наибольший уровень некратной фрактальности имеет множество из 13 вейвлетов влияния местной широты Север-Юг на местную долготу. Сравнение ранговых распределений показало, что модель (1) для широты получила 25 членов, для долготы 18 и для высоты – 12 членов.
Заключение
Гипсометрическая характеристика – важнейшее свойство рельефа. Река Ировка относится к низменному уровню, в устье высота равна 89 м, а в истоке – 148 м над уровнем моря. В статье показана возможность получения закономерностей гипсометрии.
Моделирование бинарных отношений между тремя координатами (широтой, долготой и высотой) характерных точек малой реки Ировка показало, что наибольшую квантовую определенность получает местная широта. При этом все парные закономерности имеют коэффициент корреляции более 0,95. Такая высокая адекватность волновых закономерностей показывает, что геоморфология может перейти на некратное фрактальное представление рельефа. Река Ировка отличается малым антропогенным воздействием, поэтому рельеф на длине 69 км имеет естественный характер колебательной адаптации малой реки к поверхности Вятского увала с его восточной стороны. Это позволяет перейти к анализу четырех притоков малой реки Ировка, а также моделировать рельеф всего водосборного бассейна 917 км2.
Наибольшую адекватность с коэффициентом корреляции 0,9976 получило влияние широты на долготу, то есть географическое расположение рельефа русла реки относительно геоморфологии суши на восточной стороне Вятского увала. На втором месте с корреляцией 0,9967 оказалось влияние высоты точек русла малой реки на местную долготу, и оно в основном тоже определяется рельефом Вятского увала. На третьем месте оказалось влияние широты на высоту с коэффициентом корреляции 0,9859.