В Институте геологии и природопользования Дальневосточного отделения Российской академии наук разрабатываются фторидные технологии переработки силикатного и алюмосиликатного сырья с извлечением алюминия, кремния, глинозема, кремнезема и других ценных продуктов [1; 2]. Изучаются как термодинамические вероятности, так и кинетика химических реакций [2]. Данная статья посвящена разрабатываемой нами методике математической обработки экспериментальных результатов по кинетике топохимических реакций.
Одним из основных результатов экспериментов по кинетике твердофазных химических реакций являются массивы последовательных отсчетов времени и степеней превращения исследуемого вещества при каждой из изучаемых температур. Результатами обработки являются кинетические параметры химических реакций: константы скоростей, коэффициенты формы кинетических кривых, энергии активации, а также зоны протекания и уравнения реакций. Знание этих характеристик позволяет сравнивать различные реакции, понимать условия их протекания и позволяет управлять ходом реакции.
Материалы и методы исследования
Методами исследования являются параметрический регрессионный и корреляционный анализы [3]. В качестве параметрических функций выбираем три наиболее часто использующихся уравнения:
αi = ktim, (1)
αi = 1 – exp( – ktim), (2)
αi = 1 – exp( – kti), (3)
где αi – степень превращения вещества в моменты отсчетов времени ti k – константа скорости, m – коэффициент формы кривой.
Степенной закон (1) применяется для описания топохимических реакций на участке нарастания реакции. Экспоненциальный закон (3) описывает процессы в диффузионной зоне, а также описывает реакции первого порядка [4]. Топохимическое уравнение Ерофеева-Авраами описывает реакции как в диффузионной, так и в кинетической зоне, также используется в переходной зоне при равенстве скоростей реакции и диффузии [5].
Зона реакции определяется по значению энергии активации Е. При Е < 20 кДж/моль реакция протекает в диффузионной зоне, при Е > 50 кДж/моль – в кинетической зоне. Реакцию, для которой 20 < E < 50 кДж/моль, рассматриваем протекающей в переходной зоне [2].
Выбор между параметрическими функциями при каждой температуре осуществляем по минимуму погрешностей аппроксимаций соответствующих им моделей регрессии [2]. Поскольку используемые параметрические функции нелинейны, получаемые регрессионные модели также нелинейны.
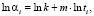 (4)
(4)
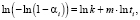 (5)
(5)
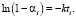 (6)
(6)
Проводя замены
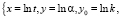 (7)
(7)
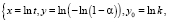 (8)
(8)
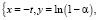 (9)
(9)
для степенного закона (7), для Ерофеева-Авраами (8) и для экспоненциального закона (9), получаем линейные уравнения со свободным членом и без свободного члена
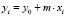 (10)
(10)
и
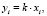 (11)
(11)
соответственно, (10) для степенного и Ерофеева-Авраами и (11) для экспоненциального закона. Значения угловых коэффициентов и свободных членов этих уравнений рассчитываются методом наименьших квадратов. Исходя из расчётных значений коэффициентов по формулам (7)–(9) рассчитываем значения параметров k, m.
Энергии активации для каждого из законов рассчитываются по уравнению Аррениуса для констант скоростей [4]
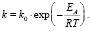 (12)
(12)
После преобразований уравнения (12) и проведения замены получим уравнение (11)
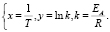 (13)
(13)
Погрешности аппроксимаций рассчитываются в соответствии с (13) по формуле
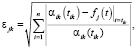 (14)
(14)
где αik(tik) – экспериментальные значения степени превращения вещества в момент времени ti при температуре Tk, 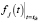 – расчетные значения функции отклика fj(t) в момент времени ti при температуре Tk.
– расчетные значения функции отклика fj(t) в момент времени ti при температуре Tk.
Расчеты погрешностей констант скоростей и коэффициентов формы кривых выполнялись в соответствии с [3]. Формулы для расчета погрешностей констант скоростей имеют вид (для (4) и (5))
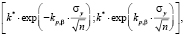 (15)
(15)
где k* – точечная оценка константы скорости, kp,β – коэффициент Стьюдента для р степеней свободы при уровне значимости β, σy – среднее квадратическое отклонение переменной y от линии регрессии, n – количество отсчетов времени.
Формулы для расчета погрешностей констант скоростей для (6) имеет вид
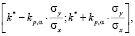 (16)
(16)
где σx – среднеквадратическое отклонение переменной x от среднего значения.
Расчеты погрешностей коэффициентов формы кривых проводятся для (4) и (5)
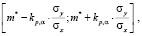 (17)
(17)
где m* – точечная оценка коэффициента формы кривой.
Погрешности расчета энергии активации вычисляются по формуле
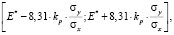 (18)
(18)
где E* – точечная оценка энергии активации. Энергии активаций, как и их погрешности, рассчитываются для каждой испытуемой функции.
Как видно, погрешности всех параметров имеют интервальные оценки. Для удобства работы с ними в программе и таблицах статьи приводятся полуинтервалы, как в случае симметричных интервалов (16)–(18), так и несимметричных (15).
В работе, кроме расчетов кинетических параметров и их погрешностей, проводится проверка ряда гипотез регрессионного и корреляционного анализов. Кратко скажем об этих гипотезах.
Статистическая проверка гипотезы об однородности дисперсии выполняется методом Снедекора-Фишера. Рассчитывается дисперсия воспроизводимости в каждой точке факторного пространства и строится F-отношение максимальной и минимальной дисперсии по всему факторному пространству 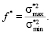 Критическое значение fβ выбирается по таблице F-распределения на уровне значимости β и числах степеней свободы h1 и h2 для
Критическое значение fβ выбирается по таблице F-распределения на уровне значимости β и числах степеней свободы h1 и h2 для 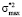 и
и 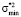 соответственно. Если f* < fβ, тогда гипотеза об однородности принимается.
соответственно. Если f* < fβ, тогда гипотеза об однородности принимается.
Для проверки гипотезы об адекватности регрессионной модели по методу Снедекора-Фишера сравнивают остаточную дисперсию 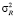 , которая вычисляется по формуле
, которая вычисляется по формуле 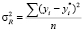 (где yi – экспериментальные значения выходной переменной, yi* – значения выходной переменной, полученные по уравнению регрессии, n – число степеней свободы), с общей дисперсией воспроизводимости
(где yi – экспериментальные значения выходной переменной, yi* – значения выходной переменной, полученные по уравнению регрессии, n – число степеней свободы), с общей дисперсией воспроизводимости 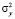 , рассчитанной по всему факторному пространству. Для сравнения используется F-отношение Снедекора-Фишера
, рассчитанной по всему факторному пространству. Для сравнения используется F-отношение Снедекора-Фишера 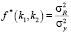 , где k1 – число степеней свободы для остаточной дисперсии, k2 – число степеней свободы для дисперсии воспроизводимости. Гипотеза об адекватности не отклоняется, если
, где k1 – число степеней свободы для остаточной дисперсии, k2 – число степеней свободы для дисперсии воспроизводимости. Гипотеза об адекватности не отклоняется, если 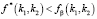 , где fβ(k1, k2) – значение в таблице F-распределения для уровня значимости β с числами степеней свободы k1 и k2 для остаточной дисперсии и для дисперсии воспроизводимости соответственно.
, где fβ(k1, k2) – значение в таблице F-распределения для уровня значимости β с числами степеней свободы k1 и k2 для остаточной дисперсии и для дисперсии воспроизводимости соответственно.
Статистическая проверка гипотезы о значимости коэффициентов регрессии выполняется по t-критерию Стьюдента. Выдвигается нулевая гипотеза о равенстве 0 коэффициента регрессии и рассчитывается статистика 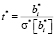 , где bi* – точечная оценка i-го коэффициента линейной регрессии,
, где bi* – точечная оценка i-го коэффициента линейной регрессии, 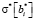 – точечная оценка стандартной ошибки для i-го коэффициента. Расчетное значение t* сравнивается с табличным значением tβ на уровне значимости β. Если t* ≥ tβ, нулевая гипотеза отклоняется и коэффициент признается значимым.
– точечная оценка стандартной ошибки для i-го коэффициента. Расчетное значение t* сравнивается с табличным значением tβ на уровне значимости β. Если t* ≥ tβ, нулевая гипотеза отклоняется и коэффициент признается значимым.
Практическая ценность полученной модели проверяется по значению коэффициента корреляции
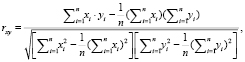
где xi и yi – координаты экспериментальных точек. Если 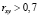 , то модель представляет практическую ценность. Значимость коэффициента корреляции оценивается по значению показателя согласованности Стьюдента
, то модель представляет практическую ценность. Значимость коэффициента корреляции оценивается по значению показателя согласованности Стьюдента 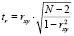 , если tr > tβ, то коэффициент корреляции значим.
, если tr > tβ, то коэффициент корреляции значим.
Результаты исследования и их обсуждение
Результаты расчета кинетических характеристик реакции фторирования гидродифторидом аммония каолинового концентрата месторождения Верхнего Приамурья в Чалганах и их погрешностей приведены в табл. 1. Расчеты погрешностей приведены для уровня значимости β = 0,05. Значения коэффициентов Стьюдента принимаются в соответствии с [6].
Выбор уравнения, которое описывает реакцию при каждой температуре, осуществляется по минимуму погрешностей аппроксимации каждой из параметрических функций экспериментальных данных. Реакция при разных температурах может описываться разными уравнениями. В нашем случае реакция описывается уравнением Ерофеева-Авраами при всех температурах. По значению энергии активации определяем зону реакции при данной температуре: в нашем случае энергия активации равна 17 кДж/моль, она меньше 20 кДж/моль, а, следовательно, зона реакции диффузионная. Уравнением реакции определяются также константа скорости и коэффициент формы кинетической кривой, рассчитанные для данной функции при данной температуре. В нашем случае значения констант скоростей принимают значения (0,0022 ± 0,0001; 0,0029 ± 0,0001; 0,0039 ± 0,0001; 0,0204 ± 0,0014) мин-1, коэффициенты формы кривых при трех нижних температурах близки к нулю (0,17; 0,16; 0,14), а при верхней температуре коэффициент формы кривой близок к 1 (0,93). Значения коэффициентов формы кривой можно оценить по рисунку, а.
Таблица 1
Результаты расчета кинетических характеристик и их погрешностей для реакции фторирования каолина Чалганского месторождения гидродифторидом аммония
|
Температура, °С |
50 |
100 |
150 |
200 |
Энергия активации, кДж/моль |
Погрешность энергии активации, % |
|
|
Вид параметрической функции |
Параметры |
||||||
|
Степенной закон |
Константа скорости, мин-1 |
0,001648 |
0,002008 |
0,002419 |
0,003903 |
7 |
33 |
|
Погрешность константы скорости, % |
4 |
1 |
1 |
5 |
|||
|
Коэффициент формы кривой |
0,13 |
0,11 |
0,08 |
0,24 |
|||
|
Погрешность коэффициента формы кривой, % |
50 |
17 |
29 |
38 |
|||
|
Погрешность аппроксимации, % |
5 |
5 |
5 |
5 |
|||
|
Уравнение Ерофеева-Авраами |
Константа скорости, мин-1 |
0,002174 |
0,002886 |
0,00391 |
0,020449 |
17 |
56 |
|
Погрешность константы скорости, % |
5 |
2 |
2 |
7 |
|||
|
Коэффициент формы кривой |
0,17 |
0,16 |
0,14 |
0,93 |
|||
|
Погрешность коэффициента формы кривой, % |
50 |
16 |
28 |
12 |
|||
|
Погрешность аппроксимации, % |
3 |
1 |
1 |
1 |
|||
|
Экспоненциальный закон |
Константа скорости, мин-1 |
0,000562 |
0,000811 |
0,000906 |
0,019188 |
25 |
72 |
|
Погрешность константы скорости, % |
81 |
38 |
56 |
23 |
|||
|
Погрешность аппроксимации, % |
80 |
77 |
79 |
3 |
|||
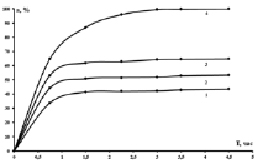
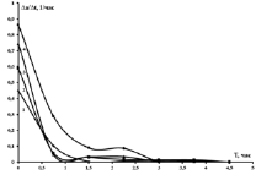
Из рисунка, а видно, что три нижних кривых выходят на плато в течение полутора часов: кривая 1 при 1,5 часа, что согласуется с точкой, в которой обращается в 0 кривая 1 на рисунке, б; кривые 2 и 3 выходят на плато уже к 1 часу, что также согласуется с поведением кривых 2 и 3 на рисунке, б; кривая 4 выходит на плато к 3 часам (рисунк, а) и обращается в 0 в этой точке (рисунка, б). Коэффициент формы кривой определяет различия в формах кривых при разных температурах, которые мы сейчас отметили. Различия констант скоростей (константа скорости для верхней температуры больше в 9, 7 и 5 раз, соответственно, константы скорости для 1, 2 и 3-й температур) определяют высоту кривой, т.е. достигнутые максимальные степени превращения: верхняя кривая лежит значительно выше, чем три нижние.
Мы обсудили значения кинетических характеристик, а также их влияние на графики кинетических кривых, но мы пока не обсуждали достоверность полученных результатов. Проведем с этой целью проверку ряда статистических гипотез. Результаты проверки статистических гипотез для уравнения Ерофеева-Авраами сведены в табл. 2. Однородность дисперсии воспроизводимости следует из того, что статистики Фишера из 3-й строки меньше, чем коэффициент Фишера из 2-й строки. Адекватность линейной регрессионной модели следует из того, что статистики из 5-й строки меньше, чем коэффициент Фишера из 4-й строки.
 а)
а)
 б)
б)
Экспериментальные кинетические кривые: a) интегральная кривая α(t); б) дифференциальная кинетическая кривая Δα(t)/Δt для реакции спекания каолинового концентрата с гидродифторидом аммония: 1 – 50 °C, 2 – 100 °C, 3 – 150 °C, 4 – 200 °C
Таблица 2
Результаты статистической проверки гипотез для уравнения Ерофеева-Авраами. Коэффициенты Фишера приводятся в соответствии с [7]
|
Температура, °С |
50 |
100 |
150 |
200 |
|
Коэффициент Фишера |
19 |
|||
|
Статистика Фишера для однородности дисперсии |
4 |
7 |
3,57 |
2,33 |
|
Коэффициент Фишера |
6,39 |
|||
|
Статистика Фишера для адекватности регрессии |
1,35 |
3,02 |
4,45 |
5,01 |
|
Коэффициент Стьюдента |
2,78 |
|||
|
Статистика для свободного члена |
29,78 |
45,15 |
6,61 |
69,63 |
|
Статистика для углового коэффициента |
5,68 |
17,68 |
10,08 |
22,81 |
|
Коэффициент корреляции |
0,92 |
0,99 |
0,97 |
0,99 |
|
Показатель согласованности Стьюдента |
4,63 |
14,44 |
8,23 |
18,62 |
Значимость коэффициентов регрессии вытекает из того, что статистики как для свободного члена из 7-й строки, так и для углового коэффициента из 8-й строки больше, чем коэффициент Стьюдента в 6-й строке. Значения коэффициента корреляции в 9-й строке > 0,7 обусловливают высокую степень связи между входными и выходными данными и, соответственно, точность предсказанного отклика. Статистическую значимость коэффициента корреляции подтверждают значения показателя согласованности Стьюдента из 10-й строки, большие коэффициента Стьюдента из 6-й строки.
Заключение
Таким образом, в данной работе апробируется методика расчета кинетических параметров: констант скоростей, коэффициентов формы кинетической кривой, энергии активации и их погрешностей, а также зоны и уравнения реакции при каждой температуре, включая статистическую проверку описанных выше гипотез регрессионного и корреляционного анализов, разрабатываемая в ИГиП ДВО РАН с целью математической обработки экспериментов по фторированию алюмосиликатов фторидами аммония.



