Известно, что интенсивность загрязнения природной среды региона и величина ущерба, наносимого экономике в результате производственно-хозяйственной деятельности, зависят от конкретных экологических характеристик рассматриваемого региона, а также от долготы, широты, высоты точек рассматриваемой местности. К настоящему времени российскими и зарубежными специалистами выполнен большой комплекс исследований по методам анализа экологических характеристик окружающей среды.
Однако такие важные и сложные проблемы современной региональной экологии, как построение и исследование уравнения динамики переноса загрязняющих примесей в различных окружающих средах с учетом их физико-химического взаимодействия, разработка методов прогноза экологической обстановки в регионе различной заблаговременности, проведение вычислительных экспериментов по исследованию и анализу сложных экологических процессов регионального масштаба и другие, по-прежнему представляют научный и практический интерес.
Большое количество публикаций, посвященных модельным задачам локальных экологических процессов переноса пассивных и активных примесей атмосферы, составляет первое направление исследований. Эти модельные задачи бедны по физическому содержанию и описывают только распространение в атмосфере аэрозолей от различных типов источников в рамках уравнений переноса и диффузии, решаются в рамках одномерной системы при заданных скоростях (например, [1]). Исследования Г.И. Марчука и его учеников во многом положили начало моделированию мезомасштабных экологических процессов на основе уравнений термогидродинамики атмосферы с учетом физико-химических превращений примесей [2].
Второе направление исследований посвящено математическому моделированию сложных экологических процессов в атмосфере регионального и глобального масштабов с использованием полных уравнений динамических и кинетических процессов [3].
Настоящая работа посвящена приложению к экологии уравнений термогидродинамики квазигеострофической и гидростатической атмосферы. Квазигеострофические и гидростатические модели успешно используются для создания на их основе глобальных климатических моделей, гидродинамической теории краткосрочного прогноза погоды. Разработаны новые версии этих моделей, обладающие высоким пространственным разрешением и адаптированные к параллельным вычислительным системам [4–6]. Отметим, что в результате численного анализа динамики крупномасштабных атмосферных процессов с помощью квазигеострофической модели установлены механизмы формирования полей метеоэлементов в атмосфере и основные закономерности атмосферных процессов регионального масштаба с приемлемой точностью [7–9]. Основные спектральные алгоритмы, а также некоторые примеры приложения спектральных методов для решения актуальных задач прикладной гидродинамики, метеорологии хорошо рассмотрены и систематизированы в [10].
Одной из главных проблем, возникающих при реализации математических моделей основных задач региональной экологии, является снижение требований к ЭВМ по быстродействию и объему памяти. Вычислительные эксперименты предложенного в работе метода аналитического расщепления показывают, что полученные приближенные решения подобного класса задач можно получить быстрее и без значительной потери точности [11, 12].
Целью настоящего исследования является реализация сложных задач региональной экологии в рамках основных уравнений динамики квазигеострофической атмосферы, позволяющая уменьшить объем вычислительных работ, необходимых для их численной реализации.
Система уравнений термогидродинамики квазигеострофической и гидростатической атмосферы
В области D = {(t, x, y, p)): t > 0, –∞ < x, y < ∞, 0 < p < p0}, состоящей из точек (t, x, y, p) прямоугольной системы координат, где t – время, (x, y) – пространственные горизонтальные координаты, p – давление, которое в дальнейшем играет роль вертикальной координаты, а неизвестной функцией становится изобарическая поверхность, рассматривается система уравнений термогидродинамики квазигеострофической и гидростатической атмосферы [13], которая после некоторых упрощающих преобразований имеет вид
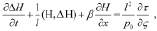 (1)
(1)
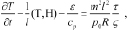 (2)
(2)
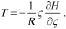 (3)
(3)
Для полученной системы уравнений термогидродинамики квазигеострофической и гидростатической атмосферы нужно определить граничные условия. В этом качестве будем использовать вертикальную составляющую вектора скорости τ, пространственный вид которой при p = p0 имеет вид
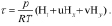
Приравнивая к нулю и произведя некоторые целесообразные поставленной задаче упрощения, получим компоненты вектора скорости в виде
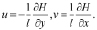
Здесь и далее использованы следующие обозначения:
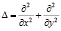 – оператор Лапласа, l – параметр Кориолиса для точек земной поверхности вдали от экватора, H = gz – новая неизвестная функция, g – ускорение силы тяжести, p – атмосферное давление,
– оператор Лапласа, l – параметр Кориолиса для точек земной поверхности вдали от экватора, H = gz – новая неизвестная функция, g – ускорение силы тяжести, p – атмосферное давление, 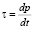 играет роль вертикальной составляющей вектора скорости, которая описывает смещение частицы воздуха относительно изобарических поверхностей, T – температура, γa – адиабатический градиент температуры, cp – удельная теплоемкость воздуха при постоянном давлении, ε – приток тепла к единице массы воздуха, который будем считать известным, R – универсальная постоянная, p0 – среднее давление на земной поверхности, принимаемое равным 1000 мб,
играет роль вертикальной составляющей вектора скорости, которая описывает смещение частицы воздуха относительно изобарических поверхностей, T – температура, γa – адиабатический градиент температуры, cp – удельная теплоемкость воздуха при постоянном давлении, ε – приток тепла к единице массы воздуха, который будем считать известным, R – универсальная постоянная, p0 – среднее давление на земной поверхности, принимаемое равным 1000 мб, 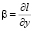 – коэффициент, учитывающий изменение параметра Кориолиса с широтой,
– коэффициент, учитывающий изменение параметра Кориолиса с широтой, 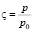 ,
, 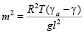 и изменяются по высоте незначительно, u, v – горизонтальные составляющие вектора скорости воздуха, (H, ΔH) и (T, H) из (1) и (2) соответственно – якобианы, вычисляемые по формуле
и изменяются по высоте незначительно, u, v – горизонтальные составляющие вектора скорости воздуха, (H, ΔH) и (T, H) из (1) и (2) соответственно – якобианы, вычисляемые по формуле
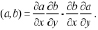
Некоторые краевые задачи физики квазигеострофической и гидростатической атмосферы
Для исследования физических закономерностей формирования и развития атмосферных процессов разных масштабов под влиянием различных факторов (например, приток тепла, орография, фазовые превращения и др.) рассмотрим некоторые краевые задачи в рамках системы уравнений (1)–(3).
Задача 1. Рассмотрим систему уравнений термогидродинамики физики квазигеострофической и гидростатической атмосферы (1)–(3) с краевыми условиями:
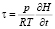 при p = p0, (4)
при p = p0, (4)
τ = 0 при p = 0.
Решение задачи 1 ищется в классе функций, ограниченных на бесконечности по горизонтальным координатам. Заметим, что задача 1 моделирует атмосферные процессы в свободной атмосфере без учета влияния процессов в пограничном слое турбулентного трения.
Для количественной оценки влияния приземного пограничного трения на эволюцию метеорологических элементов в свободной атмосфере рассматривается краевая задача:
Задача 2. Рассмотрим систему уравнений термогидродинамики физики квазигеострофической и гидростатической атмосферы (1)–(3) с краевыми условиями:
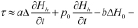
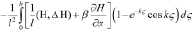
при p = ph, (5)
τ = 0 при p = 0,
где 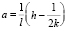 , h – толщина слоя трения, выраженная в единицах давления,
, h – толщина слоя трения, выраженная в единицах давления, 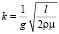 – коэффициент турбулентной вязкости в пограничном слое атмосферы,
– коэффициент турбулентной вязкости в пограничном слое атмосферы, 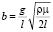 , где μ – коэффициент вертикальной турбулентной вязкости, который на практике можно определить как по данным регистрации воздушных течений, так и по данным о диффузии искусственно вводимых в атмосферу примесей.
, где μ – коэффициент вертикальной турбулентной вязкости, который на практике можно определить как по данным регистрации воздушных течений, так и по данным о диффузии искусственно вводимых в атмосферу примесей.
В настоящее время выполнен большой комплекс исследований, посвященных решению модельных задач типа (1)–(4) и (1)–(3), (5) по анализу локальных процессов, необходимых для реализации сложных и важных проблем. В результате этих исследований разработана оперативная схема краткосрочного прогноза погоды с применением ЭВМ и выявлено некорректное описание эволюции планетарных ультрадлинных волновых возмущений в атмосфере в квазигеострофическом и гидростатическом приближении, что представляет большой интерес в прогнозе погоды на длительный срок.
Модель переноса экологически вредных примесей в атмосфере региона
Рассмотрим модель переноса примесей, загрязняющих экологию атмосферы региона. Пусть вредные примеси представляют собой трехфазную смесь газа, жидкости и твердого вещества в виде аэрозолей.
Предположим, что дисперсная компонента аэрозолей представляет собой жидкие капли и твердые частицы полидисперсного спектра по величине, размеру (или объему) частиц.
Пусть ρ – плотность воздуха, а ρ1, ρ2, ρ3 – плотности вредных примесей в виде газа, жидких капель и твердых частиц в динамической атмосфере соответственно. Рассмотрим удельные величины 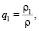
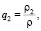
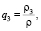 удовлетворяющие соотношению ρ1 + ρ2 + ρ3 << ρ [13].
удовлетворяющие соотношению ρ1 + ρ2 + ρ3 << ρ [13].
Упрощенная простейшая модель переноса и диффузии примесей в атмосфере региона в системе координат (t, x, y, p) имеет вид
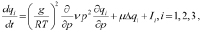
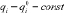 , при t = 0, qi = 0
, при t = 0, qi = 0
при p = p0, qi = 0 при p = 0,
где 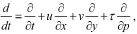 , Δ – оператор Лапласа, v, μ – коэффициенты турбулентной диффузии примесей; u, v, τ – составляющие вектора скорости переноса примесей в атмосфере; Ii – мощности источников вредных примесей с учетом физико-химического взаимодействия примесей между собой и со средой. При определении функционального вида источников примесей учитываются выпадения тяжелых жидких и твердых вредных примесей на поверхности земли путем учета величины вертикальной скорости частиц под действием силы тяжести в уравнениях переноса аэрозолей.
, Δ – оператор Лапласа, v, μ – коэффициенты турбулентной диффузии примесей; u, v, τ – составляющие вектора скорости переноса примесей в атмосфере; Ii – мощности источников вредных примесей с учетом физико-химического взаимодействия примесей между собой и со средой. При определении функционального вида источников примесей учитываются выпадения тяжелых жидких и твердых вредных примесей на поверхности земли путем учета величины вертикальной скорости частиц под действием силы тяжести в уравнениях переноса аэрозолей.
Заметим, что для задач прогноза погоды и экологии региона на сравнительно короткий срок граничные условия на поверхности земли и на верхней границе атмосферы региона будут выполняться удовлетворительно. При увеличении срока заблаговременности прогноза граничные условия могут оказаться недостаточно точными.
В этом случае граничные условия на поверхности земли можно получить на основе решения вспомогательной задачи относительно баланса примесей на границе раздела атмосфера – земля в зависимости от характера подстилающей поверхности и структуры почвы. Возможны и другие варианты постановки граничных условий переноса примесей.
Постановка задачи метода прогноза экологической обстановки в регионе
Рассмотрим постановку задачи прогноза экологической обстановки в регионе в виде двух блоков. Первый блок представляет собой задачу расчета метеорологических элементов на основе термогидродинамических уравнений в приближении квазигеострофической и гидростатической атмосферы.
Следовательно, задача, рассматриваемая в первом блоке, является методологической основой численного метода краткосрочного прогноза погоды в квазигеострофическом приближении.
Во втором блоке рассматривается задача переноса экологически вредных примесей в атмосфере региона. Совместное рассмотрение указанных двух задач представляет собой постановку задачи прогноза погоды и экологической обстановки в регионе.
Тогда полная математическая формулировка задачи совместного краткосрочного прогноза погоды и экологической обстановки в регионе в системе координат (t, x, y, p) в виде
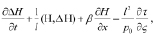
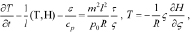
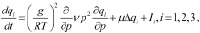
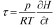 при p = p0, τ = 0 при p = 0,
при p = p0, τ = 0 при p = 0,
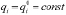 при t = 0, qi = 0
при t = 0, qi = 0
при p = 0 и p = p0.
Таким образом, задача краткосрочного прогноза погоды и экологической обстановки в регионе является сложной задачей прикладной математики, вычислительной математики и вычислительной техники. Решение расщепленных таким образом задач получено и подробно рассмотрено авторами в работе [14] с применением спектрального метода Галеркина.
Заключение
Широко распространенные конечно-разностные методы требуют проведения громоздких вычислений на каждом временном шаге, в каждой точке пространственной сетки, что влечет за собой значительное увеличение используемой оперативной памяти и замедление расчетов. Применение аналитических методов расщепления позволяет получить приближенные формулы решений для широкого класса задач, притом вычислительные эксперименты показывают, что проведение расчетов значительно ускоряется, притом без существенной потери точности. К расщепленным по физическим процессам, уже более простым задачам, можно применить спектральный вычислительный метод Галеркина, позволяющий получить приближенные решения поставленной задачи.
В заключение отметим, что в предложенных постановках краевые условия имеют довольно формальный характер, ибо оценка количества примесей, осевших близко к поверхности Земли, крайне специфична для каждой конкретно решаемой задачи.



