Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Транспортировка древесины – это важный этап лесозаготовительного процесса. Из-за отсутствия лесовозных дорог круглогодичного действия вывозка древесины с лесосек происходит по дорогам сезонного характера. По зимним лесовозным дорогам вывозится значительная часть всего объема. В летнее же время из-за воздействия неблагоприятных климатических условий вывозка затруднительна. Период эксплуатации зимних лесовозных дорог и их пропускную способность в различных природно-климатических условиях изучали многие ученые [1, 2]. Начало эксплуатации летних лесовозных дорог спрогнозировать сложнее, и исследования, посвященные данному вопросу, практически не встречаются.

Вывозка древесины в летний период производится с июля по сентябрь. Данный период характеризуют следующие факторы [3, 4]: устойчивая жаркая погода; высыхание дорог; снижение уровня грунтовых вод; улучшение несущей способности грунтов.

Эксплуатация лесовозных дорог в бесснежный период сопряжена с негативными природными воздействиями, поэтому вывозка сильно затруднена [5, 6]. Пропускная способность лесовозных дорог определяется объемом осадков. Дороги во время выпадения больших объемов осадков непригодны для перевозки грузов. Весеннее таяние снега приводит к поднятию грунтовых вод, затоплению больших лесных территорий, особенно в низменных участках, разрушению временных сооружений и т.д. [7, 8].

Кроме этого, большое влияние на начало эксплуатации летних дорог оказывает количество влаги в грунтах. В начале сезона эксплуатации летних лесовозных дорог на количество влаги в грунтах влияют не только факторы водно-теплового режима (осадки и количество осадков), но и талые воды. Задержка талых вод в грунтах зависит от промерзания почв в осенне-зимний период. Наибольшее промерзание почв происходит при большом количестве воды в почве. В результате количество осадков перед постоянно выпавшим снегом в осенний период оказывает влияние на задержку талых вод в грунтах. Таким образом, на начало вывозки леса влияют количество осадков в весенний период, положительная температура воздуха, которая способствует высыханию дорог, и количество воды в почве в осенний период [9, 2].

Цели исследования: анализ влияния осадков в весенний период, положительной температуры воздуха и количества воды в почве в предыдущий осенний период на начало вывозки леса по дорогам летнего действия и составление соответствующей регрессионной модели.

Материлы и методы исследования

В рамках настоящего исследования проведен анализ влияния природно-климатических факторов на начало вывозки леса в летний период в Енисейском районе Красноярского края Российской Федерации. Объектом исследования выступили данные о датах начала вывозки леса в летний период из территорий различных лесозаготовительных районов (Орджоникидзе, Высокогорска, Кулаково, Первомайска, Назимово). Территории различаются природно-климатическими условиями. В качестве природно-климатических факторов анализировались статистические данные за 2014–2019 гг., сведения о погоде по соответствующим метеорологическим постам. Архивные сведения погоды брались с электронного ресурса rp5.ru.

Исследовалось влияние осадков и температуры на начало вывозки леса в летний период:

– среднее суточное количество осадков с момента последнего снежного покрова до начала вывозки (x1);

– количество положительных температур с момента последнего снежного покрова до начала вывозки (x2);

– количество осадков за три недели до постоянно выпавшего снега в предыдущем году (x3).

Начало вывозки леса (на какой день летнего периода осуществлялась вывозка) будет являться результативным признаком, принимаемым за y. В табл. 1 показано, какие показатели имеют результативный признак у, и переменные x1, x2, x3.

Проведение многофакторного анализа осуществляли в среде Microsoft Office Excel.

В ходе работы проведено исследование по определению коэффициентов множественной регрессии, состоящей из нескольких переменных (независимых), являющихся компонентами следующего уравнения:

y = f(x1, x2,…, xm), (1)

где у – зависимая переменная (итоговый результирующий результат или применительно к решаемой задаче – признак); x1, x2,…, xm – независимые природно-климатические факторы (переменные для данной задачи).

Данный тип регрессионных зависимостей применяется в тех случаях, когда разнообразие воздействующих на результат факторов не позволяет выделить наиболее весомый и существует потребность в оценке влияния всех или нескольких из них [10].

Главная цель исследования – получение модели с рядом факторов, влияние которых на итоговый показатель также должно быть подвергнуто оценке.

На рис. 1 приведены статистические показатели результативного признака у и переменных x1, x2, x3. Видно значительное взаимное изменение y и независимых переменных.

Таблица 1

Данные о погодных условиях и начала вывозки древесины

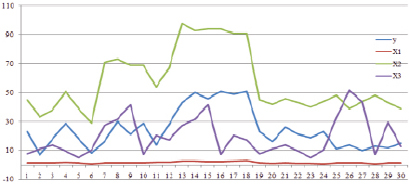
Рис. 1. Статистические данные природно-климатических условий и начала вывозки леса в летний период

Результаты исследования и их обсуждение

1. Проверка факторов на мультиколлинеарность. Выделяются следующие этапы:

– подбор факторов под сущность проблемы (исходя из опыта исследователей);

– использование формальных статистических критериев для оценки факторов. Так, для оценки корреляции необходимо определение линейного коэффициента корреляции 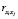. В случае, если 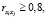то о переменных xi, xj говорят, что они находятся в линейной зависимости между собой. Тогда из этого следует, что переменные xi, xj будут являться коллинеарными.

В полученное регрессионное уравнение будет включен лишь тот коллинеарный фактор, который, обладая большой теснотой связи с результатом, будет в наименьшей степени связан с иными факторами.

В ходе работы была сформирована корреляционная матрица. Ее наполнение осуществлялось на базе функции «Данные. Анализ данных. Корреляция» известного программного продукта MS Excel.

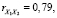
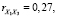
Из расчетов, представленных на рис. 2, следует, что 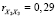. Таким образом, коллинеарность между исследуемыми факторами не наблюдается. Из рассмотрения факторы не исключаются, а регрессия будет строиться по всем трем факторам.

2. Получение уравнения линейной множественной регрессии.

Результаты приведены в табл. 2, 3, 4, при этом пропущены промежуточные этапы расчетов.

Таким образом, результаты, представленные в табл. 4, позволяют сформировать уравнение регрессии:

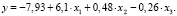(2)

3. Расчет коэффициентов множественной корреляции R и детерминации R² .

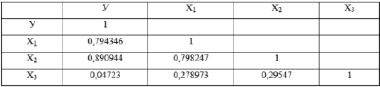
Рис. 2. Расчеты в корреляционной матрице

Таблица 2

Результаты корреляционного анализа

Таблица 3

Результаты дисперсионного анализа

Таблица 4

Результаты регрессионного анализа

Первый из них характеризует тесноту связи исследуемой подборки факторов с анализируемым признаком (результатом). Он определяется по формуле:

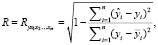(3)

где n – количество экспериментов (наблюдений); xi, yi – значения переменных; 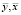– их средние значения; 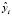– расчетные значения переменной y, вычисленные по уравнению множественной регрессии, т.е.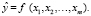

Величина коэффициента детерминации применяется при характеристике качества получаемой регрессионной модели. Более высокое значение соответствует лучшей согласованности модели с данными эксперимента или наблюдений.

Значения R и R² также можно найти в табл. 2. R = 0,93; R² = 0,87.

Коэффициент множественной корреляции изменяется от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

По шкале Чеддока можно определить, что при R = 0,93 связь весьма высокая и R² = 0,87 – высокая.

4. Проверка значимости регрессионного уравнения.

На данном этапе необходимо рассчитать фактическое значение F-критерия Fфакт (F Фишера) и сравнить его с критическим (табличным) значением F-критерия Fтабл. Если выполняется условие Fфакт > Fтабл, то уравнение считается статистически значимым.

Вычислим фактическое значение критерия по формуле:

Fфакт = 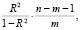(4)

где R² – коэффициент детерминации; n – число наблюдений; m – количество факторов.

Fфакт = 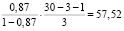. (5)

Это же значение можно было взять из табл. 3 «Статистика Фишера F».

Fтабл – это табличное значение F-критерия Фишера, соответствующее уровню значимости α и числу степеней свободы k1 = m, k2 = n – m – 1.

Расчеты в авторском исследовании показали: уровень значимости α = 0,05; а число степеней свободы k1 = 3, k2 = 30 – 3 – 1 = 26;

– Fтабл = FРАСПОБР(0,05; 3; 26) = 2,98.

При полученных Fфакт = 57,52 > Fтабл = 2,98, можно говорить о высокой значимости регрессионного уравнения, полученного в ходе исследования.

Результаты табл. 3 указывают, что значимость уравнения регрессии α = 1,3•10^-11. Очевидно, что оно существенно ниже требуемого уровня α = 0,05, т.е. уравнение значимо и при более низком уровне значимости.

5. Проведение проверки значимости коэффициентов регрессионного уравнения.

Для данного этапа исследования необходимо применение t-критерий Стьюдента. Из табл. 4 следует, что уровни значимости коэффициентов уравнения регрессии имеют значения: α_a = 0,014;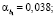

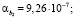
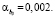
Следовательно, оценки параметров α_a; 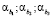значимы при уровне значимости α = 0,05.

В результате исследования определено, что дата начала вывозки леса зависит от среднего суточного количества осадков с момента последнего снежного покрова до начала вывозки. Из рис. 3 видно, что начало вывозки леса прямо пропорционально значению среднесуточного количества осадков. С увеличением количества осадков начало вывозки леса откладывается на более поздний срок. На рис. 4 представлена зависимость начала вывозки леса от количества положительных температур.

Зависимость, представленная на рис. 4, указывает на то, что с увеличением количества положительных температур начало вывозки леса откладывается на более поздний срок.

На рис. 5 представлена графическая зависимость начала вывозки леса в текущем году от количества осадков за три недели до постоянно выпавшего снега в предыдущем году.

Результаты, показанные на рис. 5, демонстрируют, что вывозка круглого леса в основном начинается при количестве осадков за три недели до постоянно выпавшего снега в предыдущем году от 8 до 37 мм.

Заключение

В ходе исследования установлена регрессионная зависимость влияния природно-климатических факторов на начало вывозки древесины с лесной территории. Выявлена закономерность изменения даты начала вывозки древесины в зависимости от природно-климатических факторов. Несмотря на то что исследования были реализованы на лесозаготовительных районах Красноярского края, полученная модель может быть использована и в других регионах страны.

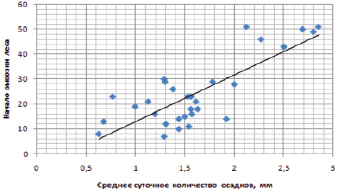
Рис. 3. Зависимость начала вывозки леса от среднего суточного количества осадков с момента последнего снежного покрова до начала вывозки

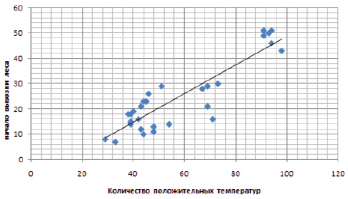
Рис. 4. Зависимость начала вывозки леса от количества положительных температур с момента последнего снежного покрова до начала вывозки

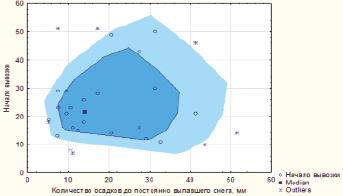
Рис. 5. Зависимость начала вывозки леса в текущем году от количества осадков за три недели до постоянно выпавшего снега в предыдущем году

Полученные результаты важны как с теоретической точки зрения, так и с практической – для планирования деятельности различных предприятий, вовлеченных в лесозаготовительный процесс.

Исследование выполнено при финансовой поддержке РФФИ, Правительства Красноярского края, Краевого фонда науки и ООО «Красресурс 24» в рамках научного проекта № 20-410-242901 и в рамках проекта «Разработка фундаментальных основ проектирования лесной инфраструктуры как динамически изменяемой системы в условиях деятельности лесозаготовительного производства», № 19-410-240005, поддержанного за счет средств целевого финансирования, предоставленного РФФИ, Правительством Красноярского края и Краевым фондом науки.