Скорость движения лесовозов при вывозке древесины с лесосеки является одним из ключевых производственных параметров [1–4]. От нее зависит максимально возможный объем заготовленной древесины. На скорость движения лесовоза влияют множество факторов.
Классификация факторов – крайне сложная задача, особенно с учетом их зависимостей и взаимообусловленностей. Тем не менее многие современные авторы успешно решают данную задачу и приводят различные примеры систематизации факторов. Одним из выводов, отмечаемым многими исследователями, следует признать необходимость осуществления заготовки и вывозки древесины в зимний период при неблагоприятных почвенно-грунтовых условиях [5–8]. Обращаясь к одному из вариантов классификации, можно разделить природно-производственные условия на две группы: внутренние и внешние. Первые из них определяются конкретной структурной схемой и организацией ее использования. В частности, ими могут быть: производственные условия, основные параметры и конструктивные особенности машин. Очевидно, что внутренние факторы напрямую зависят от способа организации производственного процесса. В то же время управление внешними крайне затруднительно, а зачастую и вовсе невозможно [9]. Вследствие этого возникает потребность минимизации их влияния [10].
Для организации наиболее эффективных мероприятий по воздействию на неблагоприятные факторы проводят факторный анализ. Он выявляет наиболее значимые параметры, на которые стоит влиять для улучшения производственных показателей.
Целью настоящих исследований является определение значимости факторов, влияющих на скорость движения автолесовоза.
Материалы и методы исследования
Существует множество методик факторного анализа. В данных исследованиях для выявления наиболее значимых факторов, влияющих на скорость лесовозов при вывозке древесины, применен метод идентификации закономерностей. Последовательность действий выполнялась по технологии [11]. Сначала приводится статистическая выборка по парам «фактор – скорость». Далее проводится идентификация нелинейного двухчленного тренда, как частного случая асимметричного вейвлета [12]. При этом в данной задаче бинарные связи появляются между факторами и одного зависимого показателя.
В процессе идентификации по принципу от простого к сложному из математических инвариантов (фрагментов) [13] составляется сложное алгебраическое уравнение. Фрагменты могут быть использованы как со знаком «+», так и «-». Инварианты колебательных возмущений в виде асимметричных вейвлет-сигналов также включают в себя конструкты как амплитуда (половина) и полупериод. По составленным уравнениям автоматически выполняется в программной среде CurveExpert-1.40 поиск значения параметров модели в виде однофакторной зависимости.
После выявления закономерностей всех пар «фактор – скорость» по значениям коэффициентов корреляции выполняется ранжирование формул по убыванию адекватности. Выбор первого в рейтинге уравнения проводится по наибольшему коэффициенту корреляции. Тогда факторы ранжируют по их значимости по мере уменьшения коэффициента корреляции.
Для построения многофакторной модели, аналогично предыдущим расчетам, составляется уравнение и производится расчет наиболее значимого фактора. Полученная зависимость записывается, а в полученные остатки, как переменная ставится второй по значимости параметр и т.д. Таким образом, просчитываются все показатели, участвующие в моделировании. Получаемое адаптивное уравнение будет являться многофакторной моделью. Все расчеты проводятся с использованием программной среды CurveExpert-1.40. По значениям коэффициентов корреляции определяется значимость и соответственно ранг параметра.
Для определения зависимости включаются следующие подсистемы с группами параметров, влияющих на скорость движения лесовоза:
– время измерения: Х1 – номер месяца в году, Х2 – номер суток в месяце, Х3 – номер часа в сутках;
– приведенные координаты участка: Х4 – широта, Х5 – долгота, Х6 – высота над уровнем моря, м;
– параметры водителя: Х7 – стаж работы водителя, лет, Х8 – возраст водителя, лет, Х9 – время в пути, ч;
– параметры лесовоза: Х10 – колесная формула автолесовоза (0 – 6х6, 1 – 6х4), Х11 – грузоподъемность автолесовоза, т, Х12 – тип кузова автолесовоза (1 – тягач, 2 – прицеп, 3 –полуприцеп), Х13 – время эксплуатации автолесовоза, лет, Х14 – мощность двигателя автолесовоза, л.с., Х15 – пробег автолесовоза, тыс. км, Х16 – время, пройденное с капремонта автолесовоза, мес., Х17 – нагруженность автолесовоза (масса груза / грузоподъемность), Х18 – тип шин на автолесовозе (0 – 425/85 r21; 1 – 14.00/r20 xml);
– характеристика дорожного покрытия: Х19 – тип покрытия дороги (0 – без покрытия; 1 – гравий; 2 – асфальт), Х20 – ширина дороги, м, Х21 – время эксплуатации дороги с момента строительства, лет, Х22 – количество капитальных ремонтов дороги с момента ее строительства, шт., Х23 – уклон дороги, %0;
– состояние покрытия: Х24 – влажность покрытия дороги (0 – сухое; 1 – влажное; 2 – сырое; 3 – мокрое; 4 – насыщенное водой), Х25 – вид снежно-ледяного покрытия дороги (0 – без снега; 1 – уплотненный снег; 2 – снежное сухое; 3 – мокрый снег; 4 – снежно-ледяное);
– метеорологические данные: Х26 – температура воздуха, °С, Х27 – атмосферное давление, мм рт. ст., Х28 – относительная влажность на высоте 2 м, %, Х29 – скорость ветра, м/с, Х30 – горизонтальная дальность видимости, км, Х31 – количество осадков, выпавших за 12 ч, мм.
Параметры объединены в группы факторов на причинно-следственной диаграмме (рис. 1).
В ходе исследования использованы данные о скорости движения автолесовозов при вывозке древесины с лесной территории на береговые нижние склады во время лесозаготовительного сезона 2019–2020 гг. по территории Мотыгинского и Енисейского лесничеств Красноярского края.
Для выявления зависимостей скорости автолесовоза от всех рассматриваемых факторов, а также многофакторной модели, выполнено 162 наблюдения, заключающихся в измерениях скорости лесовоза в различных природно-производственных условиях. Исследования проводились при условиях: участок без поворотов более 300 м, анализируемый уклон постоянный на этом участке. При этом достигается равномерная скорость на участке.
Результаты исследования и их обсуждение
С использованием программной среды CurveExpert-1.40 по каждому фактору получены однофакторные зависимости с коэффициентами корреляции. Наибольшее значение по оценке коэффициента корреляции получено у фактора Х19 (тип покрытия). В соответствии с методикой производим расчет, начиная в общем аддитивном уравнении именно с фактора Х19, затем в остатки от Х19 как переменная ставится параметр Х20 (второй по значимости) и т.д. Таким образом, учтены в последующих членах многофакторного уравнения все составляющие в рейтинге переменные.
После моделирования многофакторной модели снова был выполнен рейтинг по убыванию коэффициента корреляции у членов многофакторной модели. На диаграмме (рис. 2) представлен рейтинг по убыванию коэффициента корреляции, выполненный с учетом волновых составляющих многофакторной модели.
Наиболее значимым фактором, с сильным уровнем связи [12], оказался «Тип покрытия». Данный показатель характеризовался тремя категориями: без покрытия, грунтовое покрытие и асфальтовое покрытие. Именно эти характеристики в значительной степени влияют на скорость движения автолесовоза. Значимым фактором (слабый уровень связи) также является уклон дороги. Значимость данных факторов объясняется увеличением сопротивлений движителя при снижении качества дорожного покрытия и (или) увеличения уклона дороги.
Некоторые параметры связаны с расположением анализируемых маршрутов. Транспортные пути протягиваются от складских терминалов, которые находятся на берегах рек Ангара и Енисей, вглубь лесосырьевых баз. При этом при увеличении расстояния от терминалов увеличивается высота над уровнем моря (и, соответственно, атмосферное давление (Х27)), широта (Х4), а также ухудшается дорога (тип покрытия (Х19), ее ширина (Х20)), увеличивается время в пути (Х9).
Распределение групп факторов представлено на рис. 3.
Анализируя диаграмму, изображенную на рис. 3, а, можно сказать, что наиболее значимой является группа факторов, характеризующая дорожное покрытие. По среднему значению коэффициента корреляции (рис. 3, б) можно утверждать, что в данной группе находятся самые значимые параметры.
По суммам коэффициентов корреляции (рис. 3, а) значимыми группами факторов также являются метеорологические данные и параметры лесовоза. Однако средние значения коэффициентов корреляции группы параметров лесовоза на предпоследнем месте, что говорит об их слабой значимости.
Полученные результаты согласуются с исследованиями других авторских коллективов.
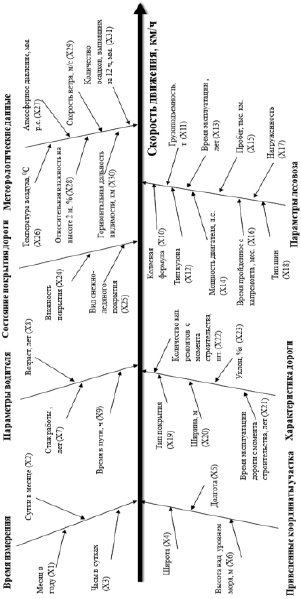
Рис. 1. Причинно-следственная диаграмма (в скобках обозначение параметра)
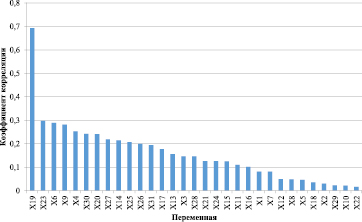
Рис. 2. Переменные, ранжированные по убыванию коэффициентов корреляции
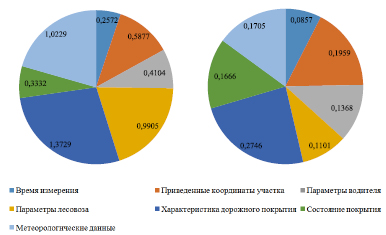
а) б)
Рис. 3. Распределение значимости групп факторов: а) по сумме коэффициентов корреляции; б) по средним значениям коэффициентов корреляции
Заключение
Представленные материалы систематизируют накопленные к настоящему времени знания по исследуемым вопросам, а также предлагают ряд новых подходов к оценке скорости лесовозного транспорта в зависимости от различных природно-производственных условий. Предложенная методика показала свою работоспособность при выявлении наиболее значимых факторов. Выявлены наиболее значимые группы факторов и отдельные параметры, влияющие на скорость лесовозного автотранспорта при вывозке древесины с лесосеки. Для дальнейших исследований, с целью снижения трудозатрат на сбор исходной информации и расчет, целесообразно многие анализируемые факторы объединить.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда науки в рамках научного проекта: «Исследование и моделирование процессов развития экономики лесной промышленности региона в контексте природно-климатических условий и ресурсного потенциала», № 18-410-240003.



