Терригенные породы, являющиеся коллекторами нефти и газа, сложены песчаниками, основным компонентом которых является кварц. Однако реальные минералы могут обладать различным количеством изоморфных примесей, различием в габитусе и дефектности кристаллической структуры.
При построении литолого-петрофизической модели залежи используют основные коллекторские свойства пород: пористость и проницаемость, однако в построении фациальной модели пласта могут помочь и другие физические свойства. Современные геологические трехмерные модели отложений учитывают фациальные условия формирования осадочных пород, исходя из данных ГИС и исследований керна скважин. Для определения количественного состава минералов и особенностей кристаллической структуры применяется рентгеноструктурный и электронномикроскопический анализы.
Типоморфные особенности кварца могут расчленять одинаковые по химическому составу пласты кварцевых песчаников, а извлеченная генетическая информация повысить информативность фациальной модели залежи.
Концепция типоморфизма минералов была введена впервые А.Е. Ферсманом. Типоморфизм – это свойство минералов в процессе образования и последующего преобразования, то есть генезиса, обладать определенными типоморфными особенностями. Поэтому в минералах имеется генетическая информация, количество которой значительно в распространенных минералах, таких как кварц, кальцит, пирит и другие.
Различают типоморфизм минералов и типоморфные особенности минералов. Стадии минералообразования характеризуются типоморфными ассоциациями минералов. Типоморфные особенности минералов разделяются на химические, структурные и физические.
Химические особенности – это наличие изоморфных примесей, изотопный состав и другое. Структурные особенности минералов – это параметры элементарной ячейки, полиморфизм, дефективность структур: плотность дислокаций, характер вакансий и другие неоднородности. В настоящей работе проводилось изучение структурных типоморфных особенностей с применением рентгенографического анализа.
Физические свойства минералов зависят от несовершенств их строения – дефектов. Дефекты подразделяют на точечные, линейные и объемные. Микроискажения возникают в связи с точечными и линейными дефектами кристаллов. Области когерентного рассеяния – это области кристалла с периодическим расположением атомов разделенными друг от друга границами зерен и дислокационными стенками. Типоморфные особенности кварца изучали ряд исследователей в России [1–3].
Цель исследования: определить параметры тонкой кристаллической структуры (размеры блоков о.к.р. и величин микроискажений) кварца различных генераций.
Материалы и методы исследования
Исследование микроструктуры, предполагающее определение размеров областей когерентного рассеяния и микроискажений, можно проводить с применением рентгеноструктурного анализа.
В работе сравниваются экспрессный рентгенодифракционный метод анализа при аппроксимации функциями Гаусса или Коши [4], Фойта [5; 6] и анализ формы профиля дифракционных линий [7] с учетом асимметрии профилей.
В случае аппроксимирующих функций Гаусса е-αx или Коши 1/(1 + γх2) по линиям 2 порядков отражения можно рассчитать размеры о.к.р. и величины микроискажений по зависимостям [4]. В экспрессном анализе используется функция Фойгта с интегральной шириной B, Коши Bк и гауссовой Bг составляющих. Значения Bк и Bг получают, применяя уравнение Лангфорда.
В ходе расчетов определяют физические уширения по Коши и Гауссу βк и βг, размер ОКР по Коши, Гауссу и общий Dк, Dг , D и величину микроискажений [6]. При расчете по функции Фойгта имеются ограничения:
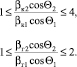 (1)
(1)
При анализе профиля [7] дифракционная линия аппроксимируется асимметричной функцией псевдо-Фойгта – суммой функций Лоренца и Гаусса.
Расчет размеров блоков D по [7] при асимметрии пика с учетом полуширины для левой и правой частей линии проводится по зависимости:
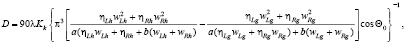 (2)
(2)
где ηR – доля функции Коши для правой доли линии;
ηL – доля функции Коши для левой доли линии;
wLg – полуширина левой доли для эталона;
wRg – полуширина правой доли для эталона;
wRh – полуширина правой доли для эксперимента;
wLh – полуширина левой доли для эксперимента;
Кк – коэффициент, характеризующий форму о.к.р.;
Θ – угол аналитической линии;
λ – длина волны излучения;
a = π – (π/ln2)1/2, b = (π/ln)1/2.
Без учета асимметрии линии при wLg = = wRg = wg и wRh = wLh = wh размер блоков вычисляется:
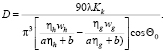 (3)
(3)
Исследования проводились на дифрактометре Thermo scientific ARL XtrA. Объектами исследований являлись образцы халцедона, яшмы, волжского агата, кварцевого песка, песчаника из керна нефтяных скважин, крупнозернистого образца кварца с коричневой окраской, отобранные в Самарской области.
Результаты исследования и их обсуждение
Рассмотрим результаты определения параметров тонкой кристаллической структуры исследованных образцов.
Для образцов халцедона и яшмы по экспериментальным уширениям B и отношению измеренной на половине высоты уширения пика к экспериментальной ширине рассчитаны уширения гауссовой и Коши компонент (табл. 1). Определялось отношение физических уширений гауссовой компоненты для двух порядков отражений βг2cosΘ2/βг1cosΘ1 и доля функции Коши ηк. Из приведенной таблицы видно, что экспериментальные уширения за счет функции Коши более значительны, чем уширения за счет функции Гаусса. Отношение βг2cosΘ2/βг1cosΘ1 для халцедона, яшмы и коричневого кварца больше допустимой величины 2, а для агата, породы, песка уширения для рефлекса 202 полностью связаны с функцией Коши, и расчет в связи с этим размера о.к.р. по функции Гаусса не имеет смысла. В связи с этим далее рассчитывался размер о.к.р. по уширениям доли Коши по зависимости 14. Отношение βг2cosΘ2/βк1cosΘ1 для большинства образцов, исключая коричневый кварц, больше 1, что допускает проведение расчетов по соответствующим зависимостям.
Для халцедона размер о.к.р. по зависимости [4] при аппроксимации по Коши составил D = 155,4 нм, а при аппроксимации по Гауссу D = 144,4 нм (табл. 2). По зависимости [6] c учетом уширения гауссовой и Коши компонент D = 127,8 нм. По зависимостям псевдо-Фойгта [7], при использовании для расчета пика 101, значение о.к.р. составило 19,8 нм, а по пику 202 значение незначительно отличается и равно D = 18,5 нм. Для образца яшмы по зависимостям [4] получены близкие по значению размеры о.к.р. D = 169,8 нм при аппроксимации по Коши. При аппроксимации по Гауссу получен размер о.к.р. D = 112,1 нм, а согласно зависимости [6] c учетом уширения гауссовой и Коши компонент D = 103,2 нм. По зависимостям [7] по пику 101 D = 17,5 нм, а по пику 202 D = 12,8 нм. Полученные значения при расчете по зависимостям российских ученых отличаются от значений, полученных по выражениям зарубежных исследователей.
Таблица 1
Экспериментальные уширения компоненты Гаусса Вг , компоненты Коши Вк, отношение физических уширений по Гауссу и Коши, доля компоненты Коши ηк образцов минералов для отражений 101 и 202
|
hkl |
Вг |
Вк |
βг2cosΘ2/βг1cosΘ1 |
βг2cosΘ2/βк1cosΘ1 |
ηк |
|
|
Халцедон |
101 |
0,070 |
0,129 |
2,62 |
1,02 |
0,83 |
|
202 |
0,153 |
0,189 |
0,93 |
|||
|
Яшма |
101 |
0,078 |
0,149 |
2,25 |
1,09 |
0,76 |
|
202 |
0,161 |
0,219 |
0,75 |
|||
|
Порода Флер. № 2 |
101 |
0,050 |
0,056 |
– |
1,36 |
0,7 |
|
202 |
0,030 |
0,108 |
0,996 |
|||
|
Порода Флер. № 6 |
101 |
0,047 |
0,073 |
– |
1,58 |
0,65 |
|
202 |
0,000 |
0,135 |
1 |
|||
|
Агат |
101 |
0,065 |
0,183 |
– |
1,07 |
0,85 |
|
202 |
0,000 |
0,265 |
1 |
|||
|
Коричневый кварц |
101 |
0,055 |
0,085 |
2,3 |
0,29 |
0,77 |
|
202 |
0,070 |
0,107 |
0,77 |
|||
|
Песок |
101 |
0,039 |
0,074 |
– |
2,75 |
0,75 |
|
202 |
0,000 |
0,185 |
1 |
Таблица 2
Физические уширения кварца β, физические уширения компоненты Коши βк, экспериментальные уширения анализируемой линии и эталона – wh, wg, размер о.к.р. D и микроискажений ε рефлексов 101 (1 пик), 202 (2 пик) кварца для образцов халцедон и яшма
|
Расчет по зависимости |
hkl |
Параметр |
Халцедон |
Яшма |
|
101 |
βк1, рад. |
0,001276 |
0,001617 |
|
|
202 |
βк2, рад. |
0,001515 |
0,002036 |
|
|
101 |
β1, рад. |
0,001139 |
0,001837 |
|
|
202 |
β2, рад. |
0,001375 |
0,002993 |
|
|
101 |
wh1, град. |
0,156 |
0,196 |
|
|
202 |
wg1, град. |
0,091 |
0,091 |
|
|
101 |
wh2, град. |
0,199 |
0,292 |
|
|
202 |
wg2, град. |
0,120 |
0,12 |
|
|
По Коши [4] |
ε |
0,000127439 |
0,00096 |
|
|
D, нм |
155,4 |
169,8 |
||
|
По Гауссу [4] |
ε |
0,00033 |
1,25E-03 |
|
|
D, нм |
144,4 |
112,0 |
||
|
По Фойгту [6] |
ε |
2,66621E-05 |
5,95E-05 |
|
|
D |
127,8 |
103,2 |
||
|
[7] |
D1(hkl = 101), нм |
19,8 |
17,5 |
|
|
D2(hkl = 202), нм |
18,5 |
12,8 |
||
Таблица 3
Рентгеновские параметры рефлекса 110 эталона кварца и халцедона для левой ветви: экспериментальная ширина пика wл, доля Коши ηл; для правой ветви: экспериментальная ширина пика wпр, доля Коши ηпр , размер о.к.р. – D
|
wл, град. |
wпр, град. |
B.05/Bл |
B.05/B пр |
ηл |
ηпр |
D, нм |
|
|
Эталон кварца |
0,110 |
0,082 |
0,844 |
0,697 |
0,038 |
0,070 |
11,1 |
|
Халцедон |
0,17 |
0,14 |
0,69 |
0,707 |
0,838 |
0,8 |
Полученные данные расчета по зависимости (2) (табл. 3) показали размер о.к.р. с учетом асимметрии линий халцедона по пику 101 D = 11.1 нм против D = 19,8 нм без учета асимметрии пика.
Для образцов агата получены близкие значения относительно яшмы и халцедона согласно зависимости [7], и для агата по пику 101 размер о.к.р составил D = 11,3 нм, а для пика 202 D = 10,2 нм (табл. 4). Для образца коричневого кварца получены значительные размеры о.к.р. исходя из зависимости [7] по 3 пикам: по пику 100 D = 174,3 нм, по пику 101 D = 52,4 нм и по пику 202 D = 117,3 нм (табл. 4).
Для образца коричневого кварца отношение βг2cosΘ2/βк1cosΘ1 менее 1, в связи с чем расчет по зависимости 14 не проводился.
Размер о.к.р. образца кварцевого песка по зависимости [7] составил для пика 101 D = 82 нм, а для пика 202 D = 36 нм (табл. 5).
Образцы кварца песчаника из керна нефтяной площади показали значительную разницу в размерах о.к.р.: образец 2 при аппроксимации по Коши составил по зависимости [4] D = 643,4 нм, а при аппроксимации по Гауссу D = 644,4 нм (табл. 5). По зависимости [6] c учетом уширения гауссовой и Коши компонент D = 642,8 нм. По зависимостям [7] при использовании для расчета пика 101 значение о.к.р. составило D = 84,0 нм, а по пику 202 значение D = 66,8 нм. Образец 6 по зависимости [4] при аппроксимации по Коши составил D = 77,7 нм, а при аппроксимации по Гауссу D = 76,1 нм. По зависимости [6] для образца № 6 c учетом уширения гауссовой и Коши компонент D = 144 нм, а по зависимостям [7], при использовании для расчета пика 101, значение о.к.р. составило 15,8 нм, а по пику 202 значение D = 10,9 нм.
Таблица 4
Физические уширения кварца β, физические уширения компоненты Коши βк, экспериментальные уширения анализируемой линии и эталона – wh, wg, размер о.к.р. D и микроискажений ε рефлексов 101 (1 пик) и 202 (2 пик), 100 (3 пик) кварца для образцов агата и коричневого кварца
|
Расчет по зависимости |
Параметр |
Агат |
Коричневый кварц |
|
βк1, рад. |
0,002203 |
0,00049 |
|
|
βк2, рад. |
0,002732 |
0,000168 |
|
|
β1, рад. |
0,002166 |
0,000339 |
|
|
β2, рад. |
0,002523 |
0,000435 |
|
|
wh1, град. |
0,215 |
0,110 |
|
|
wg1, град. |
0,091 |
0,091 |
|
|
wh2, град. |
0,265 |
0,145 |
|
|
wg2, град. |
0,120 |
0,120 |
|
|
wh3, град. |
– |
0,082 |
|
|
wg3, град. |
– |
0,078 |
|
|
По Коши [4] |
ε |
0,000154415 |
0,000063 |
|
D, нм |
78,4 |
567,7 |
|
|
По Гауссу [4] |
ε |
0,003565603 |
0,00013 |
|
D, нм |
74,9 |
505,5 |
|
|
По Фойгту [6] |
ε |
0,0000717 |
– |
|
D |
753 |
– |
|
|
[7] |
D1(2Θ = 26,6), нм |
11,3 |
52,4 |
|
D2(2Θ = 54,4), нм |
10,2 |
117,3 |
|
|
D3 (2Θ = 20,8), нм |
– |
174,3 |
Таблица 5
Физические уширения кварца β, физические уширения компоненты Коши βк, экспериментальные уширения анализируемой линии и эталона – wh, wg, размер о.к.р. D и микроискажений ε рефлексов 101 (1 пик) и 202 (2 пик) кварца для образцов № 2 и № 6 керна нефтяных скважин
|
Методика анализа |
Параметр |
Образец № 2, керн |
Образец № 6, керн |
Кварцевый песок |
|
βк1, рад. |
0,000299 |
0,001414 |
0,000464 |
|
|
βк2, рад. |
0,000470 |
0,002575 |
0,001471 |
|
|
β1, рад. |
0,000247 |
0,002103 |
0,000346 |
|
|
β2, рад. |
0,000270 |
0,002366 |
0,0004 |
|
|
По Коши [4] |
ε |
5,66023E-07 |
6,93E-05 |
2,15E-05 |
|
D, нм |
643,6 |
77,71 |
485,5863 |
|
|
По Гауссу [4] |
ε |
0,00001 |
3,2 Е-05 |
0,000572 |
|
D, нм |
642,7 |
76,1 |
466,7 |
|
|
По Фойгту [6] |
ε |
3,15E -05 |
0,000226 |
0,00021 |
|
D |
642,8 |
144,0 |
937 |
|
|
[7] |
wh1, град. |
0,105 |
0,211 |
0,098 |
|
wg1, град. |
0,091 |
0,091 |
0,078 |
|
|
wh2, град. |
0,136 |
0,256 |
0,185 |
|
|
wg2, град. |
0,12 |
0,12 |
0,162 |
|
|
D1(2Θ = 26,6), нм |
84,0 |
15,8 |
82 |
|
|
D2(2Θ = 54,4), нм |
66,8 |
10,9 |
36 |
В ряде работ [8] изучалось качество кварца в зависимости от наличия изоморфных примесей и размера кристаллов с применением рентгенографического анализа методом расчета индекса кристалличности. Расчет индекса кристалличности кварца позволяет эффективно и качественно выявить наиболее перспективные виды кварцевого сырья для получения концентратов особо чистого кварца. В [9] получены значения индекса кристалличности и размер о.к.р. для образцов кварца разного генезиса. Индекс кристалличности для представленного ограниченного ряда образцов возрастает с увеличением размеров о.к.р., и из-за недостаточной изученности физических основ индекса кристалличности и малой выборки образцов эта связь недостаточно достоверна.
Заключение
Для образцов кварца крупнозернистого песка и коричневого кварца получены большие размеры о.к.р., чем для образцов халцедона, агата и яшмы. Размеры о.к.р. образцов кварца пород керна нефтяной площади значительно различаются. Исследование параметров тонкой кристаллической структуры рассмотренными группами методов показало их некоторые преимущества и ограничения. При исследовании экспрессным методом аппроксимацией функциями Гаусса, Коши или Фойгта можно использовать линии 2 порядков отражений. Это линии с hkl-100, 200, 300, 400, 101, 202. При исследовании методом анализа формы линий не указаны ограничения в использовании любой одиночной линии из рентгенометрических данных минерала. Кроме того, расчет можно проводить по асимметричным линиям.
Размер о.к.р. с учетом асимметрии линий халцедона по пику 101 равен D = 11,1 нм. Это значение меньше размера о.к.р., полученного без учета асимметрии пика D = 19,8 нм. Результаты, полученные по зависимостям из [7] по линиям с разными hkl, отличаются друг от друга приближенно до 50 %, что сопоставимо и представляет интерес для дальнейшего изучения. В зависимостях расчета размеров блоков D методом анализа профиля линий для Kk-коэффициента, зависящего от формы о.к.р., принято значение, равное 1, исходя из предположения, что форма о.к.р. сферическая. Используя описанные методы, возможно дополнительно проводить изучение образцов кварца по размерам о.к.р. и расчленять пласты кварцевых песчаников.



