В последнее время одним из наиболее часто используемых методов практической геодезии являются ГНСС. ГНСС обеспечивают трехмерную фиксацию, по которой получается высота над эллипсоидом. Геодезические высоты – чисто математические, не имеющие физического смысла. В инженерных работах используются ортометрические высоты, т.е. высоты над геоидом. Чтобы в полной мере использовать потенциал ГНСС, необходимо установить взаимосвязь между геодезической высотой и ортометрической высотой посредством моделирования геоида. Связь между геодезической высотой (H), ортометрической высотой (Hg) и высотой геоида (ζ) задается уравнением (1), рис. 1. В Египте многие исследования в последние годы были сосредоточены на определении модели геоида для всей территории или для некоторых важных областей, например [1, 2]. Даже сейчас точное моделирование геоида остается актуальной задачей.
Hg = H – ζ. (1)

Рис. 1. Связь между высотами геодезической, ортометрической и геоида
Данные ГНСС/нивелирования обычно используются для определения высоты геоида (ζГНСС/Нив) в опорных точках и для оценки высоты геоида от ГПЗ (ζГПЗ) в этих точках [3]. Например, существует ряд исследований, посвященных изучению производительности ГПЗ [4, 5]. Для определения геоида можно использовать спутниковое нивелирование метода. Полиномиальные модели являются одной из популярных и широко используемых математических моделей. Общая форма полиномиальной модели: ζ (φ, λ) = a1φn + a2λn + . . .. . .. . .. . . Например, полином второй степени:
ζ (φ, λ) = a1 φ2 + a2 λ2 + a3 φ λ +
+ a4 φ + a5 λ + a6, (2)
где от a1 до a6 – шесть коэффициентов преобразования.
Недавно ИНС стала одним из новых методов разработки моделирования геоида, рис. 2. Elshambaky подтвердил, что многослойная нейронная сеть с прямой связью с двумя нейронами является наиболее точной из исследованных методик преобразования [6]. Albayrak сообщил, что модель геоида, идентифицированная с помощью ИНС, кажется более надежной по сравнению с моделью, рассчитанной с использованием традиционных методов интерполяции [7].
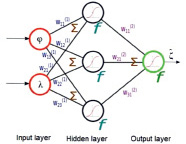
Рис. 2. Схематическое изображение ИНС
В связи с вышесказанным целью данного исследования является создание локальных моделей геоида в прибрежных территориях Средиземного и Красного морей с использованием ГНСС/ нивелирования данных от 162 опорных точек, а затем использование этих моделей для оценки точности глобальных моделей геоида, EGM2008, EIGEN-6C4 , GECO, SGG-UGM-1 и XGM2019e_2159 в исследуемых областях.
Материалы и методы исследования
Область исследования и измерения
Область исследования охватывает большинство морских побережий Египта, граничащего со Средиземным и Красным морями. Побережье Средиземного моря простирается примерно на 700 км от Сиди Баррани (31 °29'14.94"N, 26 °36'18.80"E) до побережья Северного Синая (31 °2'49.11"N, 33 °0'21.81"E). Побережье Красного моря простирается примерно на 800 км от Суэца через Хургаду (29 °47'22.98"N, 32 °26'24.40"E) до Халаеба и Шалатина (24 °12'25.52"N, 35 °25'51.29"E). На рис. 3 показан план изучаемых территорий. Район исследования на прибрежной территории Средиземного моря включал 87 реперов, а район исследования на прибрежной территории Красного моря – 75 реперов. Точные данные нивелирования были собраны с помощью точного нивелира Leica NA2 путем привязки петель нивелирования первого порядка к национальной вертикальной системе координат Египта. Погрешность ортометрических высот составляет не более ±1,0 см по отношению к ближайшим точкам государственной сети нивелирования. Кроме того, измерения GNSS для 162 реперов были выполнены относительно национальной геодезической системы координат Египта. Двухчастотные геодезические приемники Trimble 5700 использовались в относительном статическом режиме на базовой опорной станции в течение 2 ч для наблюдений каждого ровера. Геодезические высоты рассчитывались для каждой станции в каждом сеансе с погрешностью не более ± 2–3 см.
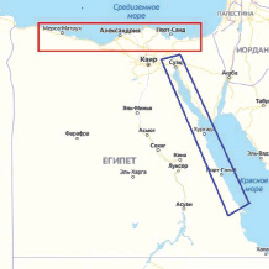
Рис. 3. Расположение зоны исследования
Методика исследования
Чтобы создать локальные модели геоида для побережья Средиземного и Красного морей, можно использовать многие методы моделирования поверхности для повышения точности модели. В этом исследовании для моделирования локальной поверхности геоида использовались методы полиномиальной регрессии и ИНС. Локальные модели геоида были созданы с использованием опорных точек (спутниковых нивелированных точек) для побережья Средиземного и Красного морей с использованием полиномиальной регрессии и ИНС. Полиномиальная регрессия и ИНС оценивались в разных вариантах. Высоты разработанного геоида рассчитывались на основе созданных локальных моделей геоида из лучших моделей. Для оценки точности высот геоида, полученных из EGM08, EIGEN-6C4, GECO, SGG-UGM-1 и XGM2019e_2159, высоты геоида из этих моделей сравнивались с высотами геоида, полученными из лучших моделей. Эти шаги более подробно описаны в следующих подразделах.
Создание локальной модели геоида с помощью метода полиномиальной регрессии
Для создания локальной модели геоида методом регрессии, вначале высоты геоида опорных точек были рассчитаны с использованием уравнения (1). После этого в процессе регрессии использовались широта и долгота точек. Использовались четыре степени полиномиальной регрессии; таким образом, четыре локальные модели геоида были получены как комбинация вариантов с использованием уравнений (3)–(6).
ζ (φ, λ) = a1 φ + a2 λ + a3, (3)
ζ (φ, λ) = a1 φ2 + a2 λ2 + a3 φ λ +
+ a4 φ + a5 λ + a6, (4)
ζ (φ, λ) = a1 φ3 + a2 λ3 + a3 φ2 λ + a4 φ λ2 +
+ a5 φ2 + a6 λ2 + a7 φ λ + a8 φ + a9 λ + a10, (5)
ζ (φ, λ) = a1 φ4 + a2 λ4 + a3 φ2 λ2 + a4 φ3 λ +
+ a5 φ λ3 + a6 φ3 + a7 λ3 + a8 φ2 λ + a9 φ λ2 +
+ a10 φ2 + a11 λ2 + a12 φ λ +
+ a13 φ + a14 λ + a15. (6)
Создание локальной модели геоида с помощью ИНС
Существуют различные модели техники ИНС, включая многослойную нейронную сеть с прямой связью, радиальную базисную сеть, сеть обобщенной регрессии и вероятностные сети. В этом исследовании для создания локальных моделей геоида был выбран вариант многослойной прямой связи, поскольку он обладает хорошими репрезентативными возможностями. Модели ИНС были созданы с использованием программного обеспечения MATLAB R2016a. В этом исследовании лучший результат был получен с двумя скрытыми слоями и десятью нейронами после тестирования нескольких различных сетевых структур. TANSIG использовался в качестве передаточной функции. Чтобы оценить точность метода ИНС для создания локальной модели геоида и в то же время для сравнения между ИНС и полиномиальной регрессией, здесь были выполнены те же 4 варианта, которые использовались с методом полиномиальной регрессии.
Оценка ГПЗ на побережьях Средиземного и Красного морей
Чтобы оценить точность EGM08, EIGEN-6C4, GECO, SGG-UGM-1 и XGM2019e_2159, высоты геоида ГПЗ (ζГПЗ) для опорных точек были получены из расчетной службы ICGEM [8]. После этого локальные высоты геоида, полученные из ГПЗ, сравнивались с локальными высотами геоида, полученными из ГНСС/нивелирования, с использованием уравнения
Δζ = ζГПЗ – ζЛ, (7)
где ζЛ – высоты геоида, полученные из лучших моделей полиномиальной регрессии или ИНС для данных ГНСС/нивелирования.
Результаты исследования и их обсуждение
Для берегов Средиземного и Красного морей были рассчитаны фактические значения высоты геоида для всех 162 опорных точек. Затем эти высоты геоида были интерполированы с использованием методов полиномиальной регрессии и ИНС для получения поверхностей, представляющих локальные модели геоидов на этих побережьях.
Локальные модели геоида для побережья Средиземного моря
Чтобы оценить точность полиномиальной регрессии и ИНС при создании локальной модели геоида на побережье Средиземного моря, были выполнены 4 локальные модели геоида с использованием φ и λ в 1-й, 2-й, 3-й и 4-й степенях. После этого значения ζГНСС\НИВ-ПР и ζГНСС\НИВ-ИНС высоты геоида из этих моделей сравнивались с ζГНСС/Нив для тех же точек. В табл. 1 представлены полученные результаты.
Таблица 1
Результаты статистического анализа ζГНСС\НИВ-ПР и ζГНСС\НИВ-ИНС, и ζГНСС/Нив на побережье Средиземного моря
|
Модели из полиномиальной регрессии |
Модели из ИНС |
|||||||
|
1-я степень |
2-я степень |
3-я степень |
4-я степень |
1-я степень |
2-я степень |
3-я степень |
4-я степень |
|
|
Среднее (м) |
0,000 |
0,000 |
0,000 |
0,000 |
0,007 |
-0,001 |
0,001 |
-0,002 |
|
СКО (м) |
0,507 |
0,209 |
0,082 |
0,060 |
0,045 |
0,032 |
0,061 |
0,035 |
|
Диапазон |
2,237 |
1,042 |
0,654 |
0,383 |
0,327 |
0,180 |
0,481 |
0,226 |
|
Минимальное (м) |
-1,154 |
-0,522 |
-0,294 |
-0,222 |
-0,070 |
-0,103 |
-0,106 |
-0,139 |
|
Максимальное (м) |
1,083 |
0,520 |
0,360 |
0,161 |
0,257 |
0,078 |
0,375 |
0,087 |
Из табл. 1 видно, что лучшей локальной моделью геоида для побережья Средиземного моря была четвертая модель при использовании φ и λ в 4-й степени полиномиальной регрессии. Кроме того, результаты показали, что лучшей локальной моделью геоида от ИНС для побережья Средиземного моря была вторая модель при использовании φ и λ в 2-й степени. Во всех четырех моделях точность, полученная с помощью ИНС, была лучше, чем точность, полученная с помощью полиномиальной регрессии.
Локальные модели геоида для побережья Красного моря
Здесь были выполнены те же шаги, что и при создании локального геоида на побережье Средиземного моря. В табл. 2 представлены полученные результаты.
Таблица 2
Результаты статистического анализа ζГНСС\НИВ-ПР и ζГНСС\НИВ-ИНС, и ζГНСС/Нив на побережье Красного моря
|
Модели из полиномиальной регрессии |
Модели из ИНС |
|||||||
|
1-я степень |
2-я степень |
3-я степень |
4-я степень |
1-я степень |
2-я степень |
3-я степень |
4-я степень |
|
|
Среднее (м) |
0,000 |
0,000 |
0,000 |
0,000 |
-0,006 |
-0,003 |
0,000 |
-0,001 |
|
СКО (м) |
0,230 |
0,198 |
0,166 |
0,162 |
0,046 |
0,043 |
0,038 |
0,041 |
|
Диапазон |
1,127 |
0,920 |
0,681 |
0,617 |
0,340 |
0,194 |
0,168 |
0,208 |
|
Минимальное (м) |
-0,554 |
-0,400 |
-0,329 |
-0,314 |
-0,201 |
-0,112 |
-0,084 |
-0,094 |
|
Максимальное (м) |
0,573 |
0,520 |
0,352 |
0,303 |
0,139 |
0,081 |
0,085 |
0,114 |
Лучшей моделью для локального геоида на побережье Красного моря с полиномиальной регрессией была четвертая модель при использовании φ и λ в 4-й степени, это показано в табл. 2. Кроме того, результаты показали, что лучшей локальной моделью геоида от ИНС была третья модель при использовании φ и λ в 3-й степени. В четырех моделях точность, полученная с помощью ИНС, была лучше, чем точность, полученная с помощью полиномиальной регрессии.
Оценка точности высот геоида, полученных из глобальных моделей геоида
Высоты геоида EGM08, EIGEN-6C4, GECO, SGG-UGM-1 и XGM2019e_2159 для всех опорных точек на побережьях Средиземного и Красного морей были получены из службы расчетов ICGEM. Затем по уравнению (7) были рассчитаны различия между ζГПЗ и ζл. Δζ-EGM, Δζ-EIG, Δζ-GEC, Δζ-SGG, Δζ-XGM – это разница между высотами геоидов из EGM08, EIGEN-6C4, GECO, SGG-UGM-1 и XGM2019e_2159 и высотами геоидов из лучших моделей соответственно. Для побережья Средиземного моря лучшим локальным геоидом была вторая модель с использованием φ и λ в 2-й степени из метода ИНС. В то время как для побережья Красного моря лучшим локальным геоидом была третья модель с использованием φ и λ в 3-й степени из метода ИНС. На рис. 4 и 5 показаны Δζ-EGM, Δζ-EIG, Δζ-GEC, Δζ-SGG, Δζ-XGM на побережьях Средиземного и Красного морей соответственно.</
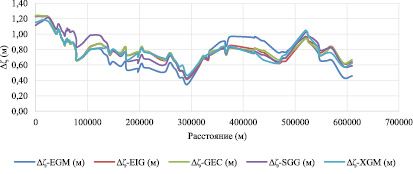
Рис. 4. Различия между высотами геоида из глобальных моделей геоида и высотами геоида из разработанной локальной модели геоида на побережье Средиземного моря
p>
В табл. 3 и 4 представлено сравнение между ζГПЗ и ζл для побережья Средиземного и Красного морей соответственно.
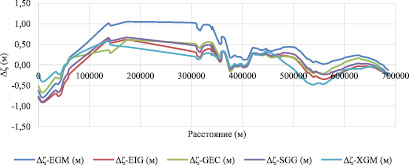
Рис. 5. Различия между высотами геоида из глобальных моделей геоида и высотами геоида из разработанной локальной модели геоида на побережье Красного моря
Таблица 3
Сравнение ζГПЗ и ζл для побережья Средиземного моря
|
EGM08 |
EIGEN-6C4 |
GECO |
SGG-UGM-1 |
XGM2019e_2159 |
|
|
Среднее (м) |
0,783 |
0,807 |
0,811 |
0,836 |
0,805 |
|
СКП (м) |
0,197 |
0,150 |
0,144 |
0,178 |
0,138 |
|
Диапазон |
0,864 |
0,793 |
0,794 |
0,733 |
0,662 |
|
Минимальное (м) |
0,376 |
0,453 |
0,458 |
0,462 |
0,504 |
|
Максимальное (м) |
1,240 |
1,246 |
1,252 |
1,195 |
1,166 |
Таблица 4
Сравнение ζГПЗ и ζл для побережья Красного моря
|
EGM08 |
EIGEN-6C4 |
GECO |
SGG-UGM-1 |
XGM2019e_2159 |
|
|
Среднее (м) |
0,313 |
0,017 |
0,106 |
0,072 |
0,031 |
|
СКП (м) |
0,386 |
0,327 |
0,261 |
0,319 |
0,266 |
|
Диапазон |
1,840 |
1,527 |
1,281 |
1,558 |
1,064 |
|
Минимальное (м) |
-0,789 |
-0,910 |
-0,669 |
-0,890 |
-0,484 |
|
Максимальное (м) |
1,052 |
0,617 |
0,612 |
0,668 |
0,580 |
Из табл. 3 видно, что на побережье Средиземного моря точность пяти моделей была близка друг к другу, но с небольшим преимуществом для XGM2019e_2159. Из табл. 4 видно, что на побережье Красного моря наблюдалось заметное превосходство точности GECO над остальными моделями.
Заключение
В последние годы одной из интересных и сложных задач в области геодезической съемки является точное определение ортометрических высот по данным ГНСС измерений. Таким образом, это исследование было предпринято для определения подходящих локальных моделей геоида для геодезических приложений на побережьях Египта. Для этого были использованы методы полиномиальной регрессии и ИНС для моделирования локальной поверхности геоида. Кроме того, была проведена оценка точности некоторых ГПЗ на побережьях Средиземного и Красного морей. Основываясь на предыдущем анализе и полученных численных результатах, точность определения локальной модели геоида на прибрежных территориях Средиземного и Красного морей с использованием ИНС было с погрешностью не более ±0,03 м и ±0,04 м соответственно. Что касается оценки ГПЗ, полученные результаты показывают, XGM2019e_2159 и GECO представляют собой самые точные из ГПЗ на прибрежных территориях Средиземного и Красного морей с погрешностью не более ±0,14 м и ±0,26 м соответственно.



