При изучении роста деревьев в конкурентной среде неизбежно возникает вопрос: как на отдельное дерево влияют его соседи? Казалось бы, всё здесь ясно и так – чем они ближе и крупнее, тем сильнее конкуренция, и тем меньше по размерам будет дерево в центре. Однако в целом ряде исследований [1; 2], в том числе в работах по конкуренции, где она изучалась многими способами, в частности в 20-летних молодняках [3] и в 184-летних насаждениях сосны [4], конкурентное давление соседей и площадь питания дерева влияли, как факторы, на размеры центрального дерева очень слабо, в пределах всего лишь 0.2–11 % [4].
Площадь питания – это простой физический фактор. Но после смыкания крон в насаждении начинает действовать ещё и фактор фитоценотический – влияние деревьев-соседей. Они могут не только конкурировать, но и «помогать» друг другу. В целом присутствует и то, и другое, и правильнее назвать их отношения взаимодействием. Они могут «давить» друг на друга (конкурировать), а могут и «дружить» друг с другом (партнёрствовать). Эти вопросы весьма актуальны в гипотезе «сильной Геи» и в эволюции биосферы на основе взаимопомощи организмов рассматриваются как основные [5].
Цель исследования: сравнить разные способы расчёта конкурентного давления и пространственных взаимодействий деревьев и выбрать лучшие из них.
Материалы и методы исследования
Для изучения пространственных взаимодействий деревьев желателен одновозрастный массив, и этому как нельзя лучше отвечают лесные культуры. Мы выбрали культуры сосны, созданные посадкой в 1967 г. на общей площади 3.3 га в кв. 43 Нижне-Курьинского участкового лесничества Пермского городского лесничества. В возрасте 55 лет они растут по 1Б классу бонитета и имеют высокую полноту. В них на относительно ровной территории заложили серию пробных площадей с нумерацией деревьев и определением их диаметра через окружность с точностью ± 0.1 см на подготовленных с подрумяниванием коры стволах на высоте 1.3 м. Деревья наносили на абрис с точностью ± 3–5 см и составляли карту их размещения в программе ArcMap-ArcView. Первоначально в 2019 г. выделили площадь 80×80 м, и её разделили на 9 пробных площадей. Но затем обнаружилось, что для выяснения ряда вопросов их нужно больше. Поэтому на следующий год нанесли на план ещё около 2 тыс. деревьев. В данной работе этот материал использован частично, и из 24 пробных площадей по всему участку выбрано 17 с высокой, средней и пониженной густотой. На них построили 1623 полигона питания вокруг живых деревьев (рис. 1).
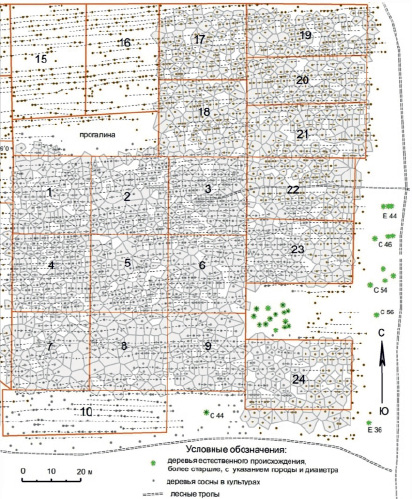
Рис. 1. Полигоны питания, доставшиеся деревьям в возрасте 30–40 лет на 17 пробных площадях в 55-летних культурах сосны. У отпавших деревьев полигоны питания показаны светлым тоном (фрагмент плана участка)
Полигоны выстраивали также для отпавших деревьев, которые находили по старым пням, и выяснили, что они отпали примерно 15–25 лет назад [6], т.е. в возрасте 30-40 лет. Площадь питания и давление соседей рассчитывали, измеряя расположение деревьев на плане. Картирование в программе ArcMap-ArcView продолжалось более года. Данные анализировали на точечных диаграммах с оценкой достоверности корреляций и применяя показатели аппроксимации трендов связей между признаками [4; 7].
Результаты исследования и их обсуждение
Использованные для анализа данные 17 пробных площадей показаны ниже (табл. 1).
Таблица 1
Некоторые таксационные показатели культур сосны в возрасте 55 лет на площади 1.25 га на 17 пробных площадях (ПП) в порядке снижения их текущей густоты
|
№ п/п |
Текущая густота, шт./га |
Средние для древостоя |
Полнота древостоя |
Число полигонов питания, шт. |
Корреляции «площадь питания×диаметр ствола», r |
||
|
диаметр, см |
высота, м |
м2/га |
относительная |
||||
|
3 |
1620 |
19.0 |
26.0 |
44.0 |
0.97 |
112 |
0.21* |
|
4 |
1530 |
18.4 |
25.7 |
45.7 |
1.01 |
109 |
0.13 |
|
2 |
1490 |
20.0 |
26.3 |
43.5 |
0.96 |
105 |
0.24* |
|
19 |
1490 |
19.4 |
26.8 |
44.1 |
0.96 |
96 |
0.31* |
|
17 |
1400 |
20.2 |
27.3 |
44.9 |
0.98 |
100 |
0.15 |
|
24 |
1390 |
20.5 |
27.5 |
46.1 |
1.00 |
129 |
0.12 |
|
20 |
1350 |
20.4 |
27.3 |
44.4 |
0.97 |
89 |
0.16 |
|
5 |
1320 |
18.8 |
25.8 |
42.3 |
0.94 |
94 |
0.16 |
|
1 |
1310 |
20.8 |
27.5 |
39.9 |
0.87 |
93 |
0.23* |
|
6 |
1270 |
20.3 |
27.6 |
46.0 |
1.01 |
90 |
0.27* |
|
18 |
1260 |
20.7 |
27.4 |
43.3 |
0.95 |
100 |
0.13 |
|
23 |
1250 |
21.6 |
27.5 |
46.0 |
1.00 |
98 |
0.25* |
|
21 |
1240 |
21.5 |
27.5 |
45.0 |
0.98 |
93 |
0.40* |
|
22 |
1230 |
20.6 |
27.4 |
41.1 |
0.89 |
95 |
0.44* |
|
9 |
1110 |
21.6 |
27.9 |
40.8 |
0.89 |
79 |
0.28* |
|
8 |
1030 |
23.1 |
28.1 |
46.5 |
1.02 |
73 |
0.46* |
|
7 |
940 |
22.5 |
28 |
39.2 |
0.86 |
67 |
0.35* |
|
Сумма |
1623 |
||||||
|
Среднее |
1308 |
20.6 |
27.2 |
43.7 |
0.96 |
0.252* |
|
|
Корреляция с текущей густотой |
– 0,87* |
– 0.79* |
0.35 |
0.40 |
– 0.57* |
||
В целом средняя корреляция между площадью питания и диаметром ствола на 17 пробных площадях равна r = 0.252 ± 0.023 и высоко достоверна при t = 10.8 > t0.99 = 2.6. Возведение её в квадрат и перевод в проценты даёт нам силу её влияния 6.4 %. Это влияние того же порядка, что и в 184-летнем сосняке, где оно равнялось 7.7 % [4]. Поэтому важен поиск любых факторов, его усиливающих. Рассмотрим влияние густоты.
На пробных площадях с малой густотой (<1308 шт./га) в большинстве случаев корреляция между площадью питания и диаметром ствола была достоверна и возрастала до значений 0.40–0.46, тогда как при густоте 1320 шт./га и выше она была достоверной только в трёх случаях из восьми. И если построить зависимость между густотами на 17 пробных площадях и корреляциями в последней графе табл. 1, то получим связь r = –0.57 ± 0.16. Для 9 «густых» пробных площадей эта корреляция в среднем равна r = 0.19, а для 8 пробных площадей в «редких» местах она возрастала в среднем до r = 0.32. При этом сила влияния фактора, рассчитанная через квадраты этих корреляций, возрастала от 3.7 до 11.4 %, т.е. увеличивалась в 3 раза.
И тут возникает парадоксальная ситуация – влияние площади питания увеличивается отнюдь не в густых местах, как это следовало бы из логики усиления там конкуренции за ресурсы и повышения роли площади питания, а наоборот, в редких местах культур. Здесь необходимо пояснить, что площадь питания в микроценозе – это обратная его густоте величина. И повышение влияния площади питания именно в редких по густоте местах чрезвычайно важно – оно показывает, что в микроценозе действие его густоты такое же, как и в целом по древостою, хотя и слабее. Так, при снижении общей густоты на 17 пробных площадях диаметры стволов в них возрастают (табл. 1), и корреляция между густотами и средними диаметрами высоко достоверна (r = –0.87 ± 0.06). Также высоко достоверно густота влияет на высоты (r = –0.79 ± 0.09). Поэтому можно полагать, что снижение густоты в сообществе деревьев полнее раскрывают их задатки, и они намного лучше используют увеличенную площадь питания.
Далее мы продолжили поиск иных факторов и задействовали диаметры стволов соседей. Этот более сложный пространственной анализ мы осуществили пока только на двух пробных площадях средней густоты и с высокой полнотой – на ПП 21 и 23.
Давление соседей в самом простом варианте можно рассчитать в виде суммы их диаметров, которую надо разделить на площадь питания центрального дерева. При этом будет получено некое «давление конкуренции» с единицей измерения см/м2. В более сложных вариантах диаметр ствола дерева-соседа делят на расстояние до центрального дерева либо умножают на ширину «контакта» с ним по стороне полигона питания. Разумеется, такой «контакт» – условная величина, но более простого способа для измерения взаимодействия между деревьями пока нет. Похожие способы в числе 8 способов измерения конкуренции использовал В.А. Усольцев [3] в молодняках сосны, изучая 20 насаждений и выбирая в каждом по 10 модельных деревьев. Однако на таких малых выборках определить лучший способ В.А. Усольцеву не удалось; не удалось его выбрать и после обзора множества работ, где эти способы применялись [8].
Поэтому рассмотрим измерение взаимодействий и конкурентное «давление» соседей на примере центрального дерева № 79 (рис. 2).
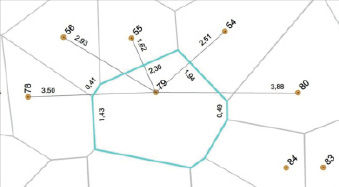
Рис. 2. Полигон питания дерева № 79 в окружении 8 соседей. Показаны расстояния до пяти соседей и «контакт» с каждым по стороне полигона питания
Здесь дерево № 79 окружают 8 соседей. Покажем пять из них, указывая диаметр их ствола, расстояние до центрального дерева и ширину «контакта» с ним:
№ 78 – 13.8 см, расстояние 3.50 м, контакт 1.43 м;
№ 56 – 17.4 см, расстояние 2.93 м, контакт 0.41 м;
№ 55 – 17.6 см, расстояние 1.62 м, контакт 2.30 м;
№ 54 – 24.5 см, расстояние 2.51 м, контакт 1.94 м;
№ 80 – 18.8 см, расстояние 3.88 м, контакт 0.49 м.
Заметим, что такие измерения можно получить без пропусков деревьев-соседей только при наличии уже построенных полигонов, где виден и каждый сосед, и ширина его «контакта» с центральным деревом. Подобные данные мы рассчитали для 190 центральных деревьев и 1069 их соседей; показатели их взаимодействия с центральным деревом показаны ниже в таблице после данных по площадям питания (табл. 2).
Таблица 2
Влияние площади питания и взаимодействия соседей с центральным деревом в 55-летних культурах сосны при относительной полноте 1.0 в результате анализа размещения 190 центральных деревьев и их 1069 соседей на пробных площадях 21 и 23
|
Взаимодействие деревьев в микроценозе |
Порядок расчётов показателя |
Единицы измерения |
Корреляция с диаметром центрального дерева |
Показатель аппроксимации линейной связи (сила влияния) |
|
1. Площадь питания 1 (до возраста 30–40 лет) |
Определение площади после выстраивания полигона через центры расстояний между соседями (включая старые пни) и центральным деревом |
м2 |
0.322 ± 0.065* |
0.103 |
|
2. Площадь питания 2 (в возрасте 41–55 лет) |
Тот же порядок расчётов, но старые пни не учитывались |
м2 |
0.368 ± 0.063* |
0.135 |
|
3 Давление диаметров стволов |
Суммируем диаметры стволов всех соседей. Делим эту сумму на площадь питания центрального дерева |
см / м2 |
0.096 ± 0.072 |
0.009 |
|
4. Взаимодействие «по расстоянию» |
Диаметр ствола соседа делим на расстояние до центрального дерева. Суммируем эти показатели |
см / м |
– 0.147 ± 0.071 |
0.022 |
|
5. Взаимодействие «по контакту» |
Диаметр ствола соседа умножаем на его контакт с центральным деревом по стороне полигона. Суммируем эти показатели от всех соседей |
см × м |
0.348 ± 0.064* |
0.120 |
Использование сложных показателей взаимодействия деревьев в микроценозе в их сравнении с простой площадью питания центрального дерева не дало существенной прибавки по корреляциям. Так, если усреднить корреляции для площади питания 1 и 2, то её значение будет равно r = 0.345, а для взаимодействия «по контакту» она равна r = 0.348.
Наиболее быстрый для расчётов способ № 4, который можно применить без выстраивания полигонов, оказался не достоверным при r = –0.147 ± 0.071 и силе влияния 0.022 или 2.2 %. Также не достоверным было давление суммы диаметров соседей при делении этой суммы на площадь питания дерева в центре, при r = 0.096 ± 0.072 и силе влияния 0.009 или 0.9 %. То есть фитоценотическое давление соседей на центральное дерево, рассчитанное двумя способами, почти на порядок оказалось ниже по своей силе (0.9–2.2 %), чем влияние площади питания, доставшейся дереву в возрасте 30-40 лет при силе влияния 0.103 или 10.3 %, а затем в возрасте 41–55 лет при силе влияния 0.135 или 13.5 %.
Наиболее интересно взаимодействие «контактное». По смыслу это получилась уже не конкуренция, а партнерское взаимодействие, так как при увеличении расстояния (ширины) контакта по стороне полигона и диаметров соседей возрастал и его результат – диаметр дерева в центре полигона увеличивался при r = 0.348 ± 0.064. Иными словами, либо каким-то образом деревья «помогали» друг другу в росте, например срастанием корней [9], либо в насаждении есть места благоприятные (где деревья согласованно увеличивали размеры) и неблагоприятные (где деревья также согласованно уменьшали свои размеры).
В связи с вышеизложенным следует освободиться от идеологемы о сильной конкуренции между деревьями, восходящей к идее «борьбы» видов за существование Ч. Дарвина [10], и взять на вооружение модели ухода с регуляцией густоты в более раннем возрасте. Для этого нужно отказаться от активных прореживаний в среднем возрасте и сместить их на возраст 10–25 лет, когда можно эффективно менять траекторию развития насаждений целевым регулированием их густоты [4].
Выводы
1. На 17 пробных площадях по 1623 деревьям корреляция между площадью питания и диаметром ствола равна r = 0.252 ± 0.023 при силе влияния фактора площади питания 6.4 %. Это влияние того же порядка, что и ранее установленное в 184-летнем сосняке (7.7 %).
2. Текущая густота культур изменялась от 940 до 1620 шт./га, и на 9 «густых» пробных площадях на 928 полигонах питания корреляция «площадь питания × диаметр ствола» была равна r = 0.19 ± 0.03, а в «редких» местах на 695 полигонах она возрастала до r = 0.32 ± 0.03. При этом сила влияния площади питания увеличивалась от 3.7 до 11.4 %, т.е. в 3 раза.
3. Влияние площади питания на диаметр ствола возрастает отнюдь не в густых местах, как это диктует парадигма конкуренции, а наоборот, в редких местах культур. Это указывает на то, что в микроценозе действие его густоты в целом такое же, как и по древостою, хотя и слабее. Так, при снижении густоты на 17 пробных площадях диаметры стволов в них возрастали при корреляции r = – 0.87 ± 0.06.
4. Взаимодействие деревьев изучали на двух пробных площадях с полнотой 1.0 на 190 полигонах тремя способами: 1) определяли давление суммы диаметров стволов соседей на единицу площади питания дерева в центре; 2) определяли взаимодействие «по расстоянию» в виде суммы диаметров соседей, делённых на расстояние до центрального дерева; 3) рассчитывали взаимодействие «по контакту», когда суммировали диаметры соседей, умноженных на длину соответствующей стороны полигона. Первые два оценивали конкурентное давление, и оно недостоверно при силе влияния 0.9–2.2 %, а третий оценивал партнёрские отношения, и их влияние достоверно при r = 0.348 ± 0.064 и силе влияния 12 %.
5. Сравнение способов оценки конкуренции между деревьями показало, что лучшим является простое определение площади питания. Более сложные способы, с расчётом давления диаметров соседей, неожиданно снижали силу её влияния.



