Появление спутниковых систем глобального позиционирования оказало огромное влияние на геодезию и инженерные приложения. Высоты, полученные с помощью глобальных навигационных спутниковых систем (ГНСС), отличаются от традиционно получаемых ортометрических высот, которые задаются относительно геоида. В результате точное определение местного геоида имеет решающее значение для геодезических приложений. Форма геоида была предметом ряда работ и исследований во всем мире [1–4].
Различные геодезические сети в Египте не охватывали всю территорию, а были сосредоточены в таких важных и населенных районах, как дельта и долина Нила и побережье Египта. Распределение по территории Египта гравиметрических и ГНСС/нивелирования пунктов неравномерно и содержит пробелы как показано на рис. 1. Следовательно, для Египта и подобных регионов надежная модель геоида с точки зрения пространственного разрешения и точности должна быть определена с использованием доступной гравиметрической информации в сочетании с высотами геоида из ГНСС/нивелирования пунктов [5].
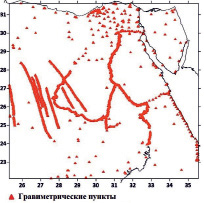
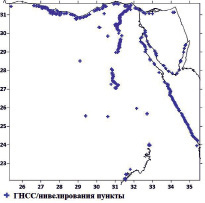
Рис. 1. Распределение пунктов гравиметрических и ГНСС/нивелирования
Одна из стандартных процедур моделирования локального гравитационного поля основана на сочетании метода удаления-восстановления и метода среднеквадратической коллокации [6]. Принцип удаления-восстановления – одна из самых известных стратегий, используемых для определения регионального и местного гравитационного поля. Он основан на предположении, что гравитационные сигналы можно разделить на длинноволновую, среднюю и коротковолновую составляющие. Длинноволновая составляющая может быть правильно учтена с помощью глобальных моделей гравитационного поля Земли (ГПЗ), которые оцениваются с использованием спутниковых наблюдений и наземных гравиметрических данных [7]. Удаление эффекта ГПЗ соответствует высокочастотной фильтрации данных. На этом этапе редукции гравитационные сигналы, обусловленные средней корой, верхней мантией и длинноволновым топографическим сигналом, удаляются из наблюдаемых значений. После сокращения для глобальной модели, помимо средних частот, в остаточных данных все еще присутствуют высокочастотные компоненты. В основном они связаны с высокочастотными особенностями топографии, которые не могут быть надлежащим образом описаны глобальными моделями [8]. Остаточный топографический сигнал удаляется из наблюдаемых данных путем вычисления так называемой модели остаточного рельефа (RTM). Остаточные данные, полученные путем применения редукции для глобальной модели и соответствующей RTM, содержат только промежуточные длины волн, которые будут использоваться для моделирования локального гравитационного поля. Обычно они имеют среднее значение, близкое к нулю, и стандартное отклонение, которое значительно меньше стандартного отклонения нередуцированных данных. К этим сокращенным данным можно подходящим образом применить совместное использование, чтобы получить оценки локальных характеристик гравитационного поля. Окончательная высота геоида затем получается путем восстановления модели геопотенциала и эффектов RTM, которые добавляются к этой локальной остаточной составляющей.
Цели данной работы: 1) оценка использования глобальных моделей EGM2008 и XGM2019e_2159 для удаления длинноволновых компонентов из аномалий силы тяжести в свободном воздухе; 2) разработка методики построения модели геоида на территории Египта путем интеграции наземных и ГНСС данных.
Материалы и методы исследования
Область исследования и измерения
Распределение гравиметрических данных неравномерно по Египту со значительными пробелами, особенно в восточных и западных пустынях. Наборы данных, используемые в исследовании, включают: 1378 гравиметрических пунктов (∆g) с СКП ± 0,2 мГал со средним расстоянием между пунктами 10 км; 455 ГНСС/нивелирования пунктов и погрешность определения высот геоида в этих пунктах не превышает 2 см, со средним расстоянием между пунктами 5 км; глобальные модели геоида (EGM2008 и XGM2019e_2159); цифровая модель рельефа SRTM30_PLUS. На рис. 1 показаны распределение пунктов гравиметрических и ГНСС/нивелирования. Для вычисления модели геоида использовался программный комплекс GRAVSOFT.
Методика исследования
1. Процесс Удаления:
Первым шагом является вычисление аномалий силы тяжести в свободном воздухе (∆gFa) и высот геоида (ζ) для наблюдаемых локальных геодезических данных вместе с соответствующими значениями, связанными с Глобальной моделью геоида. На этом этапе использовалась программа GEOEGM. Затем длинноволновые компоненты гравитационного поля Земли удаляются из ∆gFa с помощью сигнала ГПЗ (∆gГПЗ). В этом исследовании использованы глобальные модели EGM2008 и XGM2019e_2159 для представления глобальных вариаций или длин волн гравитационного поля Земли. Кроме того, очень коротковолновые составляющие гравитационного сигнала (∆gRTM) вычислены и удалены с использованием метода остаточной модели рельефа (RTM). На этом этапе среднее значение сетки получается простым усреднением с помощью программы TCGRID. Эта сетка используется позже, когда вклад RTM вычисляется с помощью программы TC. На этом этапе обработки данных входным файлом является набор данных о высоте 30" * 30", который соответствует ЦМР SRTM, покрывающей территорию Египта. В конце шага удаления, остаточные аномалии силы тяжести (∆gост) и остаточные высоты геоида (ζост), получается согласно по уравнениям (1) и (2):
∆gост = ∆gFa – ∆gГПЗ – ∆gRTM, (1)
ζост = ζГНСС/нив – ζГПЗ – ζRTM. (2)
2. Процесс Вычисления
Вычисление эмпирической и аналитической ковариационной функции
На этом этапе ∆gост использовалось для вычисления эмпирической ковариационной функции с помощью программы EMPCOV. Глобальная ковариационная функция, используемая на методе коллокации, равна тройному интегралу:
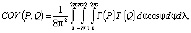 (3)
(3)
где α – азимут между P и Q и φ, λ – координаты P. Точка Q имеет фиксированное сферическое расстояние от P. Обратите внимание, что это глобальное выражение и будет зависеть от радиальных расстояний r, и rˋ точек P и Q соответственно и сферического расстояния (ψ) между двумя точками.
В локальной области мы неявно будем рассматривать все данные за пределами области как имеющие те же статистические характеристики, что и данные в области, чтобы мы могли оценить ковариационную функцию гравитационной аномалии, взяв сумму произведений данных в сгруппированной области в соответствии с интервалом Δψ сферического расстояния (также обозначаемым размером интервала выборки):
ψi – Δψ/2 ≤ ψ ≤ ψi + Δψ/2. (4)
Эти два интервала могут быть объединены, так что интервал выборки становится удвоенным. Следовательно, вычисленная ковариация равна
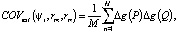 (5)
(5)
где M – количество продуктов из i-го интервала выборки, а rm – средняя высота. Ковариация будет использоваться в расчетах для обозначения средней высоты.
Определение параметров аналитических ковариационных функций
Если обнаружены отклонения степени гравитационной аномалии, то можно также найти потенциальные отклонения степени. Однако для ковариационной функции также необходимо определить бесконечно много величин. Решением этой проблемы является использование так называемой модели дисперсии степеней, то есть функциональной взаимосвязи между степенью и дисперсией степени. Чернинг и Рапп (1974) вывели три различные модели, которые можно использовать. Основное различие связано с тем, стремятся ли (потенциальные) дисперсии степеней к нулю, например, n-2, n-3 или n-4. Лучшая модель относится к типу 2 [9]:
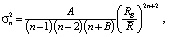 (6)
(6)
где RB – радиус сферы Бьерхаммара, A – константа в единицах (m/s)4, а B – целое число. Если используется расширение серии сферических гармоник, B обычно принимается равным небольшому числу, например 4, тогда как в исходной работе оно принималось равным 24, чтобы можно было смоделировать низкую степень и дисперсию степеней соответственно. Эта модель одновременно является Воспроизводящим Кернелом в Гильбертовом пространстве функций, гармонических вне сферы Бьерхаммара. Используемая полная модель:
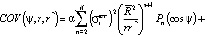
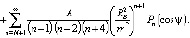 (7)
(7)
Определение высот геоида по остаточным данным
Для использования метода среднеквадратической коллокации доступны все инструменты: остаточные данные и ковариационной модели. Остальное – установить нормальные уравнения и вычислить прогнозы и оценки ошибок. Это делается с помощью программы GEOCOL. Основная функция этой программы – вычисление приближения к аномальному потенциалу Земли (T) с использованием метода коллокации. Программа GEOCOL (geocol17) запускается с выбранными гравиметрическими данными (∆gост) для прогнозирования высот геоида (δζост) и сравнивает входные и прогнозируемые значения. Набор пунктов ГНСС/нивелирования использовался в процессе подгонки поверхности созданной модели к поверхности пунктов ГНСС/нивелирования, а остальные пункты использовались для оценки внешней точности модели.
3. Процесс Восстановления
На этом этапе влияние остаточной топографии с использованием программы TC и вклад глобальной модели с помощью программы GEOEGM восстановлены и добавлены к прогнозируемой δζост в расчетных пунктах, чтобы получить окончательную высоту геоида (ζF) как
ζF = δζост + ζГПЗ + ζRTM. (8)
Результаты исследования и их обсуждение
Выбор наиболее совместимой глобальной гравитационной модели имеет большое влияние на вычисление геоид в районах, страдающих от отсутствия однородных и точных данных о гравитационных аномалиях. В этом исследовании были использованы глобальные модели EGM2008 и XGM2019e_2159 для удаления длинноволновых компонентов из аномалий силы тяжести в свободном воздухе.
1. Процесс Удаления
Данные табл. 1 показывают, что удаление длинноволновых компонентов (∆gГПЗ) из аномалий силы тяжести (∆gFa) приводит к существенному сглаживанию, о чем свидетельствует уменьшение СКП на 38 % и 36 % при использовании EGM2008 и XGM2019e_2159 соответственно.
Таблица 1
Статистика аномалий остаточной силы тяжести [мГал]
|
Модель EGM2008 |
Модель XGM2019e_2159 |
|||||||
|
Среднее |
СКП |
Мин. |
Макс. |
Среднее |
СКП |
Мин. |
Макс. |
|
|
ΔgFa |
-10.38 |
18.31 |
-67.69 |
110.72 |
-10.38 |
18.31 |
-67.69 |
110.72 |
|
ΔgFa- ΔgGGM |
0.85 |
11.63 |
-55.28 |
72.80 |
0.90 |
11.75 |
-28.68 |
31.16 |
|
ΔgFa- ΔgGGM- ΔgRTM |
1.63 |
11.93 |
-53.08 |
70.45 |
1.68 |
12.05 |
-27.38 |
34.28 |
2. Процесс Вычисления
∆gост использовались в качестве входных данных для программы EMPCOV для вычисления эмпирической ковариационной функции. Для лучшей корреляции на основе расстояния между данными было определено, что идеальное сферическое расстояние (ψ) составляет 10 угловых минут. Фактическое моделирование эмпирически определенных значений выполняется с помощью программы COVFIT и было вычислено аналитическое представление для эмпирической ковариационной функции. При использовании программы COVFIT трем параметрам ковариации α, A и RB сначала даются приблизительные значения, а затем с помощью итерационной нелинейной регулировки для определения окончательных параметров ковариационной функции (Knudsen, 1988). На рис. 2 показаны эмпирические и аналитические подобранные ковариационные функции EGM2008 и XGM2019e_2159.
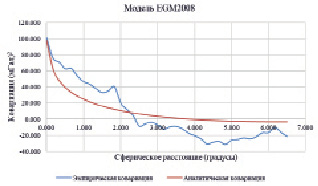
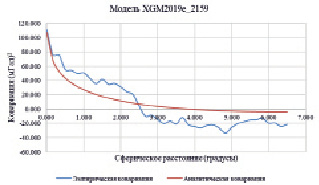
Рис. 2. Эмпирические и аналитические подобранные ковариационные функции
Следующие параметры ковариации при использовании EGM2008 и XGM2019e_2159 были получены и применены в процессе коллокации: RB = –5.586 км и -3.088 км, Дисперсия силы тяжести на нулевой высоте 100.78 мГал2 и 111.78 мГал2, масштабный коэффициент дисперсии степени ошибки 1.00. Эти параметры использовались для расчета δζост.
355 пунктов ГНСС/нивелирования использовались в процессе подгонки поверхности созданной модели к поверхности пунктов ГНСС/нивелирования, а 100 пунктов использовались для оценки внешней точности модели. Сравнение между прогнозируемыми остаточными высотами геоида δζост и ζост в 355 пунктах ГНСС/нивелирования показано в табл. 2.
Таблица 2
Статистика прогнозируемых и наблюдаемых высоты геоида в 355 пунктах ГНСС/нивелирования (использованы в процессе подгонки)
|
Модель EGM2008 |
Модель XGM2019e_2159 |
|||||||
|
Среднее |
СКП |
Макс. |
Мин. |
Среднее |
СКП |
Макс. |
Мин. |
|
|
Наблюдения (м) |
-0.643 |
0.375 |
1.536 |
-1.707 |
-0.581 |
0.394 |
0.695 |
-1.532 |
|
Прогнозы (м) |
-0.643 |
0.367 |
1.533 |
1.708- |
-0.581 |
0.388 |
0.676 |
-1.531 |
|
Разница (м) |
0.000 |
0.071 |
0.288 |
-0.350 |
0.000 |
0.060 |
0.246 |
-0.375 |
Результаты показывают различия между прогнозируемой и наблюдаемой высотой геоида с ошибкой около ± 7 см и ± 6 см при использовании EGM2008 и XGM2019e_2159 оответственно.
3. Процесс Восстановления
Остающийся шаг моделирования геоида включает: 1) восстановление эффекта остаточной топографии с помощью программы TC; и 2) восстановление вклада глобальных ГПЗ EGM2008 и XGM2019e_2159 с помощью программы GEOEGM. Сетка точек (5ˋ x 5ˋ) была извлечена из ЦМР SRTM30_PLUS для прогнозирования высот геоида в этих точках программой Select. Затем программа Fcomp использовалась для расчета окончательных высот геоида (ζF) для этих точек сетки в соответствии с уравнением 8. Результаты модели геоида представлены на рис. 3 в виде трехмерных графиков распределения высот геоида при использовании EGM2008 и XGM2019e_2159 соответственно.
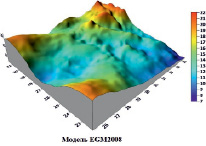
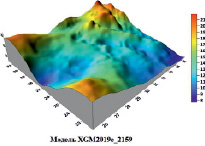
Рис. 3. Графическое представление ЦМГ для территории Египта
Оценка окончательной модели геоида
Чтобы проверить точность созданной модели геоида для территории Египта, высоты геоида из 100 пунктов ГНСС/нивелирования (ζГНСС/нив), которые не были включены в процесс моделирования геоида, сравнивались с соответствующей высотой геоида этих пунктов из модели (ζF). Результаты статистически проанализированы и представлены в табл. 3.
Таблица 3
Статистика прогнозируемых и наблюдаемых высот геоида в 100 пунктах ГНСС/нивелирования (использованы для оценки внешней точности модели)
|
Модель EGM2008 |
Модель XGM2019e_2159 |
|||||||
|
Среднее |
СКП |
Макс. |
Мин. |
Среднее |
СКП |
Макс. |
Мин. |
|
|
Наблюдения (м) |
-0.609 |
0.400 |
1.370 |
-1.225 |
-0.573 |
0.390 |
0.538 |
-1.257 |
|
Прогнозы (м) |
-0.596 |
0.428 |
1.500 |
-1.252 |
-0.570 |
0.383 |
0.442 |
-1.175 |
|
Разница (м) |
-0.014 |
0.107 |
0.209 |
-0.472 |
-0.003 |
0.079 |
0.195 |
-0.221 |
Результаты показывают различия между прогнозируемой и наблюдаемой высотой геоида с ошибкой около ± 11 см и ± 8 см при использовании EGM2008 и XGM2019e_2159 соответственно.
Заключение
Для Египта разработана новая национальная модель геоида с использованием интеграции имеющихся гравитационных аномалий и ГНСС данных. Чтобы выполнить решение задачи создания модели геоида на территории Египта, и был применен метод коллокации из-за способности использовать гетерогенные данные в качестве входных. Результаты показывают, что внешняя точность моделей геоида по сравнению с независимыми пунктами ГНСС/нивелирования составляла с СКП равно ± 11 см и ± 8 см при использовании EGM2008 и XGM2019e_2159 соответственно. Окончательная национальная модель геоида для всех территорий Египта представлена в виде цифровой модели геоида (ЦМГ) с сеткой точек (5ˋ x 5ˋ). Модель XGM2019e_2159 показала лучшие результаты в Египте, чем модель EGM2008, с точки зрения удаления длинноволновых компонентов из аномалий силы тяжести. Количество и распределение гравиметрических и ГНСС/нивелирования пунктов в Египте недостаточно. Поэтому рекомендуется установить дополнительные пункты, чтобы заполнить недостающие пробелы в информации о гравитации. Следует продолжить усилия по моделированию геоида, чтобы создать национальную сантиметровую модель геоида, которая заменит традиционные, трудоемкие и дорогостоящие методы нивелирования.
Исследователь Елшеви М.А. финансируется за счет частичной стипендии Министерства высшего образования Арабской Республики Египет.



