Колебательная адаптация существует в природе, включая живое и косное вещества по В.И. Вернадскому. Этот принцип адаптации действует и на социумы, например в виде субъектов федерации. Тогда получается, что закон Коммонера «всё связано со всем» исходит из взаимных колебаний процессов адаптации, которые проявляются в виде суммы асимметричных вейвлетов [1]. Коллективные действия необходимы, чтобы отвести земную систему от порога глобального экологического кризиса. Такие действия включают управление системой Земли – биосферой, климатом и обществами – на уровнях изменений поведения [2].
Доход населения также является важным фактором. Неравномерное распределение доходов оказывает давление на окружающую среду как со стороны самого низкого, так и самого высокого уровня доходов. Чтобы просто выжить, многие из беднейших людей мира участвуют в нерациональном использовании ресурсов. Они также вынуждены истощать скудные природные ресурсы, такие как леса или популяции животных, чтобы прокормить свои семьи [3].
Экологические инновации в «зеленых» технологиях становятся основным фактором экономического роста, при этом происходит неравномерное развитие этих инноваций и технологий в разных странах мира [4]. В статье рассмотрены стратегические риски отставания России от ведущих в экономике стран.
Цель исследования – иерархия по коэффициенту корреляции трендов [1] влияния 40 параметров у 14 субъектов Урала и Сибири на долю населения ниже прожиточного минимума, методика коэффициента неравномерности Джини по кривой Лоренца, принятой в виде тренда.
Материалы и методы исследования
По исследованиям [5] за 2014–2019 гг., на протяжении четырех лет начиная с 2014 г., в России наблюдалось снижение реальных располагаемых денежных доходов населения. Коэффициент Джини уменьшился с 0,419 до 0,412, что свидетельствует о незначительном снижении неравенства доходов населения.
Иерархия влияющих переменных была составлена по результатам факторного анализа 40 параметров у 14 субъектов Урала и Сибири. Всего было получено 1600 уравнений в виде закономерности (1), из которых 1360 относятся к парным отношениям. Как зависимый показатель на первом месте оказался фактор Х33 – доля населения ниже прожиточного минимума, % (табл. 1). По иерархии уменьшения коэффициента корреляции как влияющая переменная на первом месте оказался фактор – использование воды, м3/чел. После воздуха потребление воды для человека является второй первичной потребностью.
Таблица 1
Влияющие факторы на показатель Х33 – доля населения ниже прожиточного минимума, %
|
Ранг R |
Код x |
Коэф. кор. r |
Наименование влияющего параметра |
|
0 |
Х33 |
0,9940 |
доля населения ниже прожиточного минимума ( %) по рангам |
|
1 |
Х19 |
0,9527 |
использование воды, м3/чел. |
|
2 |
Х37 |
0,9461 |
средние душевые доходы населения, руб/мес. |
|
3 |
Х01 |
0,9356 |
приведенная северная широта центра столицы, |
|
4 |
Х32 |
0,9263 |
уровень безработицы, % |
|
5 |
Х28 |
0,9141 |
младенческая смертность на 1000 родившихся живыми |
|
6 |
Х27 |
0,8944 |
суммарный коэффициент рождаемости |
|
7 |
Х11 |
0,8777 |
сумма осадков за июль 2018 г., мм |
|
8 |
Х08 |
0,8607 |
средняя месячная температура в январе 2018 г., °С |
|
9 |
Х21 |
0,8598 |
выбросы в атмосферу, кг/чел. |
|
10 |
Х17 |
0,8316 |
общий экологический коэффициент |
|
11 |
Х36 |
0,8310 |
ВРП на душу населения за 2018 г., тыс. руб/чел. |
|
12 |
Х03 |
0,8244 |
высота центра столицы над уровнем Балтийского моря, м |
|
13 |
Х26 |
0,8165 |
ожидаемая продолжительность жизни женщин, лет |
|
14 |
Х30 |
0,8104 |
естественный прирост на 1000 населения |
|
15 |
Х14 |
0,8100 |
доля пашни к площади суши, % |
|
16 |
Х40 |
0,8086 |
число умерших женщин в возрасте 16–54 лет на 105 населения |
|
17 |
Х24 |
0,7999 |
ожидаемая продолжительность жизни всех, лет |
|
18 |
Х07 |
0,7996 |
среднее число в месяц дней с осадками > 0,1 мм (1961–1990) |
|
19 |
Х31 |
0,7800 |
уровень занятости, % |
|
20 |
Х39 |
0,7717 |
число умерших мужчин в возрасте 16–59 лет на 105 населения |
|
21 |
Х35 |
0,7528 |
доля сельского населения, % |
|
22 |
Х04 |
0,7527 |
средняя месячная ночная температура (1961–1990), °С |
|
23 |
Х16 |
0,7432 |
доля измененных человеком угодий к площади суши, % |
|
24 |
Х34 |
0,7388 |
доля городского населения, % |
|
Окончание табл. 1 |
|||
|
Ранг R |
Код x |
Коэф. кор. r |
Наименование влияющего параметра |
|
25 |
Х25 |
0,7142 |
ожидаемая продолжительность жизни мужчин, лет |
|
26 |
Х22 |
0,5907 |
улавливание выбросов в атмосферу, кг/чел. |
|
27 |
Х10 |
0,5677 |
сумма осадков за январь 2018 г., мм |
|
28 |
Х20 |
0,5647 |
сброс загрязнений в воду, м3/чел. |
|
29 |
Х23 |
0,5331 |
плотность населения, чел/км2 |
|
30 |
Х02 |
0,5284 |
приведенная восточная долгота, причем |
|
31 |
Х09 |
0,5241 |
средняя температура в июле 2018 г., °С |
|
32 |
Х06 |
0,5015 |
средняя сумма осадков (1961–1990), мм |
|
33 |
Х05 |
0,4922 |
средняя дневная температура (1961–1990), °С |
|
34 |
Х38 |
0,4697 |
умершие оба пола в трудоспособном возрасте на 105 населения |
|
35 |
Х18 |
0,3959 |
забор воды, м3/чел. |
|
36 |
Х29 |
0,3931 |
коэффициент миграционного прироста на 104 населения |
|
37 |
Х12 |
0,3681 |
доля сельхозугодий к площади суши, % |
|
38 |
Х13 |
0,3059 |
доля лесов к площади суши, % |
|
39 |
Х15 |
0,2479 |
доля растительности «трава + кусты + деревья» к суше, % |
Доля растительного покрова от суши почти не влияет на долю населения ниже прожиточного минимума. Однако [3] бедное население влияет на снижение растительности.
Кривая Лоренца является методом графического изображения уровня концентрации явления. Математически эта кривая описывается трендом.
Все модели бинарных отношений были выявлены по формуле
y = aexp(–bxc) + dxeexp(–fxg), (1)
где y – показатель, x – влияющая переменная, a – g – параметры (1) двухчленного тренда, идентифицируемые в среде CurveExpert-1.40. Второй член соответствует кривой Кузнеца.
Коэффициент Джини вычисляется относительно кривой Лоренца. При этом, если кривая Лоренца характеризуется общим уравнением двухсоставного тренда (1), то появляется возможность разработки методики расчета коэффициента Джини.
На рис. 1 приведен график уравнения (1) для влияния среднедушевых доходов населения на долю населения ниже прожиточного минимума для 14 субъектов федерации.
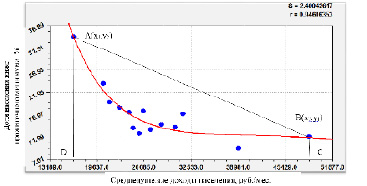
Рис. 1. Схема к расчету коэффициента Джини неравномерного влияния среднедушевых доходов на долю населения ниже прожиточного минимума: S – стандартное отклонение; r – коэффициент корреляции
Кривой Лоренца становится график уравнения (1). Но, в отличие от общепринятой методики расчета неравномерности распределения мы примем не диагональ от 0 до 1, а конкретные граничные значения (минимумы и максимумы) влияющей переменой x на изменение зависимого показателя y.
Тогда линия АВ будет линией равномерного распределения. Трапеция ABCD покажет теоретический объем равномерного распределения. В этом случае площадь под кривой Лоренца в интервале от x1 до x2 будет характеризовать фактический объем неравномерного распределения. Тогда отношение площади фигуры кривой Лоренца до прямой линии AB (числитель) к площади трапеции ABCD (знаменатель) станет коэффициентом Джини.
Рассмотрим обратное парное отношение (рис. 2) между этими же параметрами. Здесь картина усложнилась: второй слева субъект получил больший среднедушевой доход.
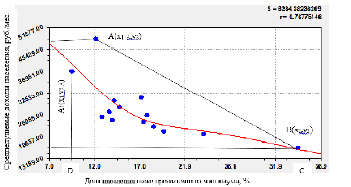
Рис. 2. Схема к расчету коэффициента Джини обратного влияния доли населения ниже прожиточного минимума на среднедушевые доходы
Опыт моделирования показал, что переход от точки A1 к более высокой по оси ординат точке А показывает волновой подъем значения показателя по асимметричному вейвлету.
Результаты исследования и их обсуждение
Для одного показателя и множества переменных в табл. 1 приведены 39 влияющих параметров на долю населения ниже прожиточного минимума. Из математической статистики известно, что в таком случае мерой неравномерности распределения становится стандартное отклонение S, которое автоматически выводится в программной среде CurveExpert-1.40.
В табл. 2 приведены параметры модели (1) для всех влияющих переменных.
Таблица 2
Параметры тренда (1) доли населения ниже прожиточного минимума и стандартное отклонение от влияния разных переменных
|
Ранг R |
Код x |
Коэф. кор. r |
Экспоненциальный закон |
Биотехнический закон |
Станд. откл. S |
|||||
|
a |
b |
c |
d |
e |
f |
g |
||||
|
1 |
Х19 |
0,9527 |
247,1966 |
0,00084935 |
1 |
-173,4034 |
0,057818 |
0,0010665 |
1 |
2,251 |
|
2 |
Х37 |
0,9461 |
516,1222 |
4,54980e-5 |
1 |
-3,31655 |
0,53959 |
6,62654e-5 |
1 |
2,400 |
|
3 |
Х01 |
0,9356 |
1,96104e6 |
4,46699 |
0,30697 |
-4,04202e6 |
0,16996 |
5,20013 |
0,29277 |
2,966 |
|
4 |
Х32 |
0,9263 |
11,06136 |
-0,021548 |
1 |
0,039664 |
2,29383 |
0 |
0 |
2,649 |
|
5 |
Х28 |
0,9141 |
41,09944 |
0,30629 |
1 |
0,037217 |
2,99788 |
0 |
0 |
2,850 |
|
6 |
Х27 |
0,8944 |
3,88416 |
-0,834432 |
0,88638 |
32,52691 |
9,90786 |
2,51978 |
2,50719 |
3,757 |
|
7 |
Х11 |
0,8777 |
16,44231 |
2,74932e-5 |
2,06631 |
0,064596 |
11,53535 |
0,017520 |
1,06918 |
4,026 |
|
8 |
Х081 |
0,8607 |
9,99330e5 |
1,16173 |
0,58811 |
-1,03564e6 |
0,25614 |
1,40071 |
5,63718 |
4,277 |
|
9 |
Х21 |
0,8598 |
21968,99 |
0,0022284 |
1 |
-21910,02 |
0,0005339 |
0,0022341 |
1 |
3,784 |
|
10 |
Х17 |
0,8316 |
16,49388 |
0,032043 |
1 |
0,0097469 |
2,00118 |
0 |
0 |
3,904 |
|
11 |
Х36 |
0,8310 |
28707,78 |
0,0014637 |
1 |
-22188,86 |
0,0044737 |
0,0014756 |
1 |
4,122 |
|
12 |
Х03 |
0,8244 |
13,99281 |
-0,0006371 |
1 |
8,6131e-38 |
13,66546 |
0 |
0 |
3,978 |
|
13 |
Х26 |
0,8165 |
705,53701 |
0,00060270 |
1 |
-8,04954 |
1,23451 |
0,012435 |
1 |
4,278 |
|
Окончание табл. 2 |
||||||||||
|
Ранг R |
Код x |
Коэф. кор. r |
Экспоненциальный закон |
Биотехнический закон |
Станд. откл. S |
|||||
|
a |
b |
c |
d |
e |
f |
g |
||||
|
14 |
Х302 |
0,8104 |
14,65075 |
-0,0090517 |
1 |
8,2048e-28 |
21,65281 |
0 |
0 |
4,118 |
|
15 |
Х14 |
0,8100 |
436,9968 |
0,20190 |
0,56916 |
-566,8485 |
0,21060 |
0,55589 |
0,44460 |
4,927 |
|
16 |
Х40 |
0,8086 |
13,89734 |
-0,00050076 |
1 |
7,703e-115 |
44,75396 |
0 |
0 |
4,135 |
|
17 |
Х24 |
0,7999 |
1034,8541 |
-0,0055406 |
1 |
-10,76146 |
1,36119 |
0,012008 |
1 |
4,447 |
|
18 |
Х07 |
0,7996 |
77,87132 |
-0,00026476 |
1,57491 |
-5,33149 |
0,63472 |
0 |
0 |
4,449 |
|
19 |
Х31 |
0,7800 |
495,48864 |
0,0097055 |
1 |
-0,52297 |
2,16570 |
0,044095 |
1 |
4,636 |
|
20 |
Х39 |
0,7717 |
91,76271 |
0,00057999 |
1 |
75,81e-136 |
45,34476 |
0 |
0 |
2,939 |
|
21 |
Х35 |
0,7528 |
7,81816e10 |
1,69061 |
1 |
0,35638 |
1,30429 |
0,022285 |
1 |
4,877 |
|
22 |
Х043 |
0,7527 |
8,77390e-8 |
-17,06038 |
0,044176 |
-4,7959e-5 |
7,52045 |
4,38224 |
0,33150 |
5,531 |
|
23 |
Х16 |
0,7432 |
32655,89 |
1,48449 |
0,17180 |
-4,28887,4 |
0,034072 |
1,76232 |
0,16206 |
5,621 |
|
24 |
Х34 |
0,7388 |
13,63130 |
-0,026993 |
1 |
-0,0005945 |
2,75619 |
0 |
0 |
4,736 |
|
25 |
Х25 |
0,7142 |
584,41677 |
-0,0012761 |
1 |
-7,25376 |
1,29477 |
0,019788 |
1 |
5,186 |
|
26 |
Х22 |
0,5907 |
26,75275 |
-0,00023247 |
1 |
-1,13134 |
0,41979 |
0 |
0 |
5,672 |
|
27 |
Х10 |
0,5677 |
23,19547 |
0,011778 |
1 |
-5,749e-15 |
0,23589 |
1,96318 |
1 |
6,099 |
|
28 |
Х20 |
0,5647 |
23,22734 |
-0,0029644 |
1 |
-0,29644 |
0,96725 |
0 |
0 |
5,801 |
|
29 |
Х23 |
0,5331 |
21,55956 |
-0,024806 |
1 |
-0,99309 |
1,03409 |
0 |
0 |
5,947 |
|
30 |
Х02 |
0,5284 |
5,14063 |
-0,016437 |
1 |
6,39911 |
0,15393 |
0 |
0 |
5,968 |
|
31 |
Х09 |
0,5241 |
0,69175 |
-0,32229 |
1 |
-1,6362e-6 |
6,46521 |
0 |
0 |
5,986 |
|
32 |
Х06 |
0,5015 |
33,05282 |
0 |
0 |
-0,078449 |
0,87912 |
0 |
0 |
5,798 |
|
33 |
Х05 |
0,4922 |
1,45113 |
0,063030 |
1 |
-3,6539e-9 |
5,65311 |
0 |
0 |
6,118 |
|
34 |
Х38 |
0,4697 |
-0,0040772 |
0,00028413 |
1 |
0,0086862 |
1,20059 |
0 |
0 |
6,205 |
|
35 |
Х18 |
0,3959 |
6723,2324 |
0,0015142 |
1 |
-6675,1053 |
0,0010532 |
0,0015231 |
1 |
6,804 |
|
36 |
Х294 |
0,3931 |
11,81876 |
-0,027780 |
1 |
-0,037033 |
1,48044 |
-0,016461 |
1 |
6,813 |
|
37 |
Х12 |
0,3581 |
13,60576 |
-0,036640 |
1 |
-0,0087807 |
2,30113 |
0 |
0 |
6,563 |
|
38 |
Х13 |
0,3059 |
8,49712 |
-0,032785 |
1 |
-0,0002227 |
2,97493 |
0 |
0 |
6,692 |
|
39 |
Х15 |
0,2479 |
1,77343 |
-0,046817 |
1 |
-8,8003e-9 |
5,15361 |
0 |
0 |
6,810 |
Примечания: Х08 – 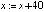 ; Х30 –
; Х30 – 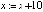 ; Х04 –
; Х04 –  ; Х29 –
; Х29 –  .
.
При условии c = 1 первая составляющая (1) превращается в закон Мандельброта (в физике), Лапласа (в математике), Перла – Ципфа (в биологии) и Парето (в эконометрике). Переменная Х27 получает модифицированный закон Мандельброта. При этом биотехнический закон в Х27 идентичен форме кривой Кузнеца. При отрицательном знаке перед второй составляющей она становится кризисной, препятствующей росту показателя. При условиях f = 0 и g = 0 биотехнический закон превращается в степенную функцию.
Оценка неравномерности иерархии из 39 влияющих параметров по стандартному отклонению показала, что разница между ними три раза.
Для случая многих показателей даже два из них имеют разные значения. Предлагаем коэффициент неравномерности, равный отношению стандартных отклонений формулы (1) и среднеарифметического y0 = a (рис. 3).
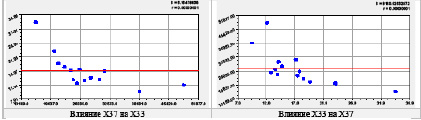
Рис. 3. Графики среднеарифметических значений двух показателей
Для важнейшей пары Х37–Х33 (рис. 3) получаем среднее арифметическое a = 17,1 %, при этом по табл. 2 S = 2,400 %. Из рис. 3 видно, что S0 = 6,165. Тогда коэффициент неравномерности K для показателя Х33 будет равен K = 2,400 / 6,165 = 0,3893. А для пары Х33–Х37 (рис. 3) будет a = 27535,1 руб/мес., а на рис. 2 видно, что S = 6284,3 руб/мес., а на рис. 3 стандартное отклонение среднеарифметического равно S0 = 8160,5 руб/мес. Коэффициент неравномерности будет равен 6284,3 / 8160,5 = 0,7701. Тогда в 0,7701/ 0,3893 = 1,98 ≈ 2 раза по линии неравномерного распределения предпочтительнее пара Х37–Х33 в сравнении с парой Х33–Х37.
Оказалось, что кривая Лоренца является в общем случае многокомпонентным уравнением, содержащим, кроме тренда, дополнительные колебания. Например, вейвлет-анализ динамического ряда температуры воздуха за 1959–2017 гг. дал 188 составляющих, из которых первые две составляющие относятся к тренду, а остальные 186 – к асимметричным колебаниям. При этом каждая составляющая является квантом поведения приземного слоя воздуха в процессе колебательной адаптации атмосферы. Причем все они распределяются фрактально по модифицированному закону Мандельброта по критерию стандартного отклонения.
Распределение коэффициента корреляции
Далее рассмотрим, как распределяются влияющие 39 переменных по коэффициенту корреляции из табл. 1 внутри иерархии. При этом ранговое распределение Х33 по двухсоставному тренду характеризуется коэффициентом корреляции 0,9940. В табл. 1 дадим ему ранг 0.
После идентификации вейвлета было получено (рис. 4) уравнение вида
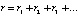 , (2)
, (2)
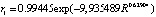 ,
,
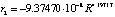 ,
,
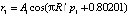 ,
,
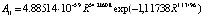 ,
,
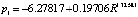 .
.
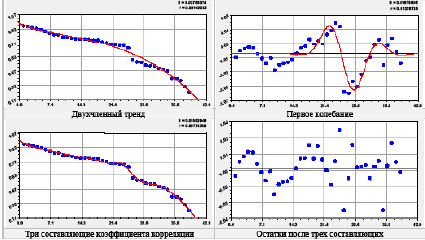
Рис. 4. Графики распределений коэффициента корреляции по рангам в иерархии влияющих переменных
Тренд является частным случаем вейвлета, поэтому из остатков видно, что возможно идентифицировать четвертое и последующие колебания. Первый член получает модифицированный закон Мандельброта, который показывает на фрактальное распределение переменных, влияющих на один показатель Х33 – доля населения ниже прожиточного минимума, %.
В итоге доказана квантовая определенность параметров социумов в виде населения субъектов федерации. В дальнейшем возможна идентификация вейвлетов для всей России.
Заключение
Предложена система из 40 факторов жизнедеятельности населения 14 субъектов федерации Урала и Сибири, соотнесенная с географическими координатами (широтой и долготой) и высотой над уровнем Балтийского моря центров столиц этих же субъектов федерации. Обособленно рассмотрено влияние этих факторов как влияющих переменных на показатель в виде доли населения ниже прожиточного минимума. В факторном анализе этот показатель занял первое место в иерархии. Затем влияющие переменные были расставлены в рейтинге по убыванию коэффициента корреляции двухчленного тренда.
Выполнено сравнение кривой Лоренца по взаимообратному влиянию доходов населения (социумов) на долю ниже прожиточного минимума. Тогда коэффициент Джини неравномерности распределения превращается в статистические показатели в виде стандартного отклонения и коэффициентов корреляции.
Показано, что для коэффициента неравномерности пары переменные – показатель применяются стандартные отклонения, а для многих показателей учитывают отношения стандартных отклонений идентифицированной формулы к средней арифметической. Все закономерности имеют квантовую определенность в процессах колебательной адаптации социумов. Кванты поведения имеют фрактальные распределения по модифицированному нами закону Мандельброта.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда науки в рамках научного проекта: «19-45-240004р_а Прогноз эколого-экономического потенциала возможных «климатических» миграций в Ангаро-Енисейском макрорегионе в меняющемся климате 21-го века».




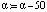
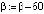 , °
, °