Решение многих практических и научно-технических задач, связанных c изучением современных движений земной коры и поверхности, оценкой техногенных деформационных процессов и устойчивостью прецизионных сооружений, основано на использовании значимых и репрезентативных результатов повторных геодезических измерений. Успешное решение таких задач на современном этапе осложняется наличием в результатах повторных высокоточных нивелирований грубых погрешностей, которые часто соизмеримы с определяемыми значениями величин смещений и их скоростей. Особо следует отметить, что грубые погрешности, присутствующие в результатах повторного нивелирования, не только резко снижают эффективность их использования при мониторинге деформационных процессов, но и способствуют принятию ошибочных решений по управлению контролируемых негативных последствий, обусловленных развитием этих процессов. К причинам возникновения в результатах повторного высокоточного нивелирования следует отнести быстроизменяющиеся, нерегулярные изменения внешних условий, в которых выполняется нивелирование, нарушения методики нивелирования исполнителями и допущенные ими ошибки.
Выполненные исследования на геодинамических полигонах разрабатываемых месторождений показали, что результаты повторного нивелирования в соответствии с соответствующими нормативными документами и инструкциями отягощены в суровых климатических условиях Крайнего Севера по объективным и субъективным причинам грубыми погрешностями, обусловленными следующими основными факторами:
– сдвижениями переходных точек при различных затратах времени на прокладку прямых и обратных нивелирных ходов на фоне развития гидротермических движений земной поверхности и морозного пучения высокодисперсных грунтов;
– смещения штативов на нивелирных станциях;
случайными наклонами нивелирных реек;
– нивелирной рефракцией, порождаемой неустойчивой температурной страти- фикацией;
– ошибочным выбором места постановки нивелирной рейки при использовании в качестве нивелирного пункта скважин нефтегазовых промыслов или конструктивных элементов инженерных объектов;
– различия в освещении нивелирных реек и температурных деформациях разных частей нивелирных реек.
Традиционно влияние таких грубых ошибок на результаты повторного нивелирования ослаблялось на основе анализа этих результатов исполнителем в соответствии с традиционными рекомендациями, приведенными в «инструкции по нивелированию I, II, III и IV классов».
На современном этапе применения автоматизированных систем геодезических измерений и математической обработки их результатов проблема оценки влияния и исключения грубых погрешностей нивелирования обострилась. Так при выполнении измерений электронными нивелирами к традиционным грубым ошибкам добавляются грубые ошибки наведения на нивелирную рейку, фиксации отсчетов по нивелирной рейке, искаженная нумерация мест постановки нивелирных реек и другие [1].
Полученная информация с помощью электронного нивелира, отягощенная грубыми погрешностями, предварительно не обрабатываемая и не анализируемая исполнителем, поступает в массив данных, подтверждающийся математической обработкой, основанной на классических способах уравнивания методом наименьших квадратов. В традиционной теории математической обработки геодезических измерений, в том числе результатов повторного нивелирования, проблеме установления наличия грубых ошибок и их исключения отводилась незначительная роль [1–3]. Поэтому необходимо дальнейшее совершенствование в геодезическом производстве процедуры поиска и исключения грубых ошибок из результатов геодезических измерений и, в частности, повторного высокоточного нивелирования. Одним из прогрессивных путей решения такой проблемы является поиск и исключение грубых ошибок в процессе уравнительных вычислений.
Целью исследования является внедрение нетрадиционного подхода к уравниванию результатов высокоточных геодезических измерений с позиций метода наименьших модулей (МНМ) [4, 5]. В рамках решаемой задачи требуется определить k значений неизвестных величин из n (n > k) линейных уравнений:
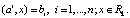 (1)
(1)
Метод позволяет исключить влияние грубой ошибки в измерениях на результат уравнивания, что позволит увеличить надежность и репрезентативность интерпретации результатов измерений.
Материалы и методы исследования
Уравнивание выполняется традиционно по методу наименьших квадратов (МНК), согласно которому измеренные величины получают поправки vi, удовлетворяющие условию [pv2] = min, где pi – вес результата измерений. При этом применяют параметрический и коррелатный способы уравнивания. Коррелатный способ предусматривает составление r (r = n – k) условных уравнений на n неизвестных истинных значений измеренных величин. То есть составляются уравнения не на k (k > n) неизвестных параметров, а на n неизвестных истинных значений измеренных величин, представляющих собой собственно линейные комбинации k неизвестных параметров.
Параметрический способ базируется на системе уравнений n поправок. Основные уравнения коррелатного способа уравнивания можно представить как (n – 2) линейных комбинаций из n уравнений поправок параметрического способа. Таким образом, коррелатный способ уравнивания, так же как и параметрический, сводится к нахождению k неизвестных параметров.
Различие параметрического и коррелатного способов уравнивания состоит в том, что в параметрическом способе определяются k неизвестных значений из n уравнений (n > k), а в коррелатном эти же k неизвестных параметров определяются из r = n – k уравнений, рассматриваемых как условные уравнения при минимизации некоторой функции от n переменных, что делает ее функцией от k неизвестных. Следовательно, оба способа уравнивания являются эквивалентными и сводятся к поиску k неизвестных из n при (n > k) соотношений, что и составляет задачу уравнивания.
Результаты исследования и их обсуждение
Система уравнений поправок (1) является переопределенной и чаще всего не имеет решения (традиционно), поэтому ставится задача минимизации какой-либо формы от невязки (несоответствие измеренных величин известному математическому условию).
При параметрическом способе уравнивания поправки vi представлены как реализация помех геодезических измерений в их результатах. В соответствии помех при измерениях n – k уравнения поправок системы (1) являются линейными комбинациями из k независимых уравнений этой же системы.
Эту же задачу можно свести к задаче линейной регрессии типа
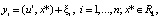 (2)
(2)
где по yi (искаженные помехой xi) и известным входным величинам ui оценивается вектор х*. Как известно [6], для решения регистрационных задач применяют метод максимального правдоподобия, здесь укажем лишь, что для нормального распределения помех метод максимального правдоподобия совпадает с методом наименьших квадратов. Известная [7] теорема Гаусса – Маркова, в основе которой лежит метод наименьших квадратов, утверждает, что оценка искомых неизвестных МНК обладает наименьшей среди всех линейных несмещенных оценок матрицей ковариаций независимо от закона распределения помехи. Однако для других (отличных от нормального) законов распределения оценка МНК не является эффективной. Следовательно, МНК является асимптотически эффективным лишь в случае нормального закона распределения помехи, когда оценки МНК являются оценками максимального правдоподобия.
Согласно [7], оценки максимального правдоподобия, как и МНК при нормальном распределении помехи, не являются устойчивыми к отклонениям закона распределения помехи от предполагаемого.
Рассмотрим последние утверждения на примере. Оценкой максимального правдоподобия скалярной величины х0 по m измерениям 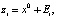 где Ei – независимые случайные величины, нормально распределенные со средним 0 и дисперсией 1, является среднее арифметическое
где Ei – независимые случайные величины, нормально распределенные со средним 0 и дисперсией 1, является среднее арифметическое 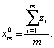
Представленная оценка имеет наименьший второй момент среди любых несмещенных оценок для случая нормального распределения помех. Пусть одно измерение zi из m измерений zm распределено иначе. Тогда и у оценки 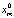 дисперсия будет значительной по величине. Такие ситуации сопровождает высокоточное повторное нивелирование, выполненное в циклах наблюдений на геодинамических полигонах (отказ нивелира, смещение костыля и нивелирного знака, ошибочное наблюдение нивелирной рейки и т.д.). Такие события встречаются при строгом соблюдении программы нивелирования редко, но оказывают решающее влияние на оценку xm.
дисперсия будет значительной по величине. Такие ситуации сопровождает высокоточное повторное нивелирование, выполненное в циклах наблюдений на геодинамических полигонах (отказ нивелира, смещение костыля и нивелирного знака, ошибочное наблюдение нивелирной рейки и т.д.). Такие события встречаются при строгом соблюдении программы нивелирования редко, но оказывают решающее влияние на оценку xm.
Швейцарский статистик Хубер [8] предложил путь исключения таких осложнений. Считая, что истинная плотность помехи р неизвестна (известным является лишь класс, которому она принадлежит), Хубер указал оценки, работоспособные для всех р из этого класса. При естественных предположениях такие оценки являются асимптотически мини-максными на класс, то есть в известном смысле [6] оптимальными. Приведем Хуберовские оценки для двух наиболее важных классов. Если pm – класс всех нивелирных распределений, то
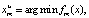
где
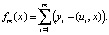
То есть поскольку о распределении ничего не известно, то следует применять метод наименьших модулей. Если р – класс «приближенно нормальных» распределений, то
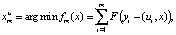
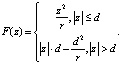 (3)
(3)
Параметр d в математических выражениях (3) зависит от «уровня загрязнения» основного (нормального распределения). Следовательно, если распределение близко к нормальному, то необходимо пользоваться «промежуточным» между МНК и МНМ методом. Следовательно, использование МНМ предоставляет возможности «застраховаться» от влияния грубой ошибки измерений, когда о распределении помехи ничего не известно. Следует учитывать, что МНК в этой ситуации может дать оценку неизвестного вектора параметров, непригодную для научно-практического использования в геодинамической и геомеханической интерпретации результатов повторного нивелирования [9].
Рассмотрим результаты уравнивания элементов нивелирной сети, представленной на рисунке.
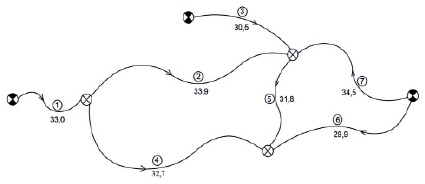
Схема сети нивелирных ходов
При параметрическом способе уравнивания система уравнений поправок (1) имеет следующий вид
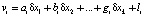 ,
,
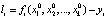 ,
,
где 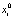 – близкие (приближенные) к точным значениям измеряемых параметров.
– близкие (приближенные) к точным значениям измеряемых параметров.
В таблице представлены значения поправок dх, полученных по рекуррентным схемам МНК и МНМ при трех рядах значений невязок lkj (k = 1, … ,6; j = 1, 2, 3) и соответствующих им дисперсиям невязок di. Представленные результаты показывают, что при уменьшении «дисперсии невязок» значения поправок dх1, dх2, dх3, полученных по рекуррентным схемам МНК и МНМ, сближаются, а при увеличении «дисперсии невязок» в значениях поправок наблюдаются значительные расхождения. Так как о распределении погрешностей в рассматриваемом примере ничего не известно, то для уравнивания, с позиций научной корректности и эффективности результатов уравнивания, целесообразно применить рекуррентный метод наименьших модулей [9, 10]. Справедливость данной рекомендации по выбору метода для уравнивания результатов нивелирования также подтверждается следующими обстоятельствами. В рассматриваемой нивелирной сети геодинамического полигона при равных длинах ходов и периметров полигонов нивелирования получены значительные расхождения в невязках от 0,9 до 8,5 мм, что позволяет предположить наличие отклоненной от нормального закона распределения ошибок нивелирования. Это частично подтверждается данными уравнивания, полученными по МНК и МНМ.
Результаты уравнивания
|
Ряд невязок li, мм |
Метод уравнивания и значения поправок δx |
|
|
МНК |
МНМ |
|
|
Дисперсии невязок δi, мм |
δx1, δx2, δx3 |
δx1, δx2, δx3 |
|
0,0; 1,7; 0,0; 8,5; 4,9; 0,0; -0,9 12,37 Критерий МНК = 25,56 Критерий МНМ = 9,40 |
-2,57 -0,82 3,30 |
-2,00 -0,30 4,50 |
|
-1,0; 1,2; -1,3; 1,4; 1,1; -1,2; 1,5 1,41 Критерий МНК = 1,81 Критерий МНМ = 2,79 |
-1,48 -1,30 -0,62 |
-2,13 -1,33 -0,72 |
|
0,0; 1,65; 0,0; 8,5; 4,8; 0,0; 0,9 12,35 Критерий МНК = 25,56 Критерий МНМ = 9,42 |
-2,56 -0,82 3,31 |
-1,97 -0,32 4,48 |
Заключение
Таким образом, применение традиционно используемых для решения подобного рода задач методов, относящихся к математической обработке результатов повторных высокоточных геодезических наблюдений, в основе которых лежит метод наименьших квадратов, не является полностью обоснованным и единственным безальтернативным подходом. Приведенные результаты и требования нормативных материалов, накладываемые на методику проведения повторного высокоточного нивелирования, показывают, что применение метода наименьших модулей, в дополнение к методу наименьших квадратов, позволяет повысить качество, репрезентативность и релевантность результатов повторного высокоточного нивелирования, за счет снижения влияния систематических ошибок повторного высокоточного нивелирования и позволяя исключить их или учесть на стадии обработки его результатов.



