Тепловой фактор во многих, практически интересных случаях оказывает существенное влияние на выбор обоснованных и надежных технических и технологических решений при проектировании, строительстве и эксплуатации подземных и наземных сооружений криолитозоны различного назначения [1–3]. Главным образом это связано с зависимостью прочностных свойств дисперсных мерзлых пород от температуры. Известно, что при повышении температуры, даже в диапазоне отрицательных значений, прочность горных пород снижается. По данным многочисленных лабораторных исследований, выполненных в нашей стране и зарубежными учеными, эта зависимость близка к квадратичной. То есть, например, чтобы прочность пород на сжатие увеличить в два раза, надо понизить их температуру в четыре раза (в пределах отрицательных значений, естественно). Для снижения прочности нужно, наоборот, повышать температуру горных пород. Кроме того, известно, что при оттаивании отдельных видов дисперсных пород прочность может достигать нулевых значений [4–6]. Поэтому получение достоверной информации о процессах формирования теплового режима горных пород, окружающих выработки конкретного подземного сооружения, является важным элементом проектирования, позволяющим обоснованно выбрать параметры крепи, обеспечивающие заданную степень надежности эксплуатации горных выработок в течение всего нормативного срока существования подземного сооружения. Наиболее представительным показателем, который обычно используется при проектировании для выбора вида и параметров крепи, является глубина оттаивания (радиус оттаивания) горных пород вокруг выработок. Например, выбор параметров анкерной крепи для горных выработок рудников криолитозоны напрямую определяется глубиной оттаивания дисперсных пород [1, 7, 8]. Как правило, замок анкера должен размещаться в мерзлых породах. Если значение глубины оттаивания превышает длину анкеров, применяемых на руднике, то используют другой вид крепи, например арочную металлическую крепь. Естественно, что капитальные затраты при этом существенно увеличиваются. Этот пример показывает практическую важность реальной оценки глубины оттаивания пород вокруг выработок подземных сооружений криолитозоны. В настоящее время разработаны мощные программные комплексы для прогноза теплового режима горных пород и грунтовых оснований, при наличии процессов промерзания-оттаивания, которые используются при выборе проектных решений, например [9, 10]. Наиболее перспективными являются программные комплексы «FROST 3D» и «COMSOL Multiphysics», которые позволяют моделировать широкий круг прикладных задач строительной и горной теплофизики и постоянно совершенствуются. Однако они не всегда доступны обычным инженерным работникам горных и строительных предприятий, которым приходится принимать оперативные решения по обеспечению надежности конкретных подземных объектов в период эксплуатации. Поэтому получение простых аналитических зависимостей для прогноза температурного режима горных пород и, в частности, глубины оттаивания пород вокруг горных выработок, является актуальной задачей горной теплофизики, которой уделяется должное внимание в научном и инженерном сообществе [11–13].
Целью настоящей работы является оценка точности приближенной формулы для определения безразмерного радиуса оттаивания горных пород вокруг выработок цилиндрической симметрии в подземных сооружениях криолитозоны.
Материалы и методы исследования
Для достижения цели воспользуемся методологией, изложенной нами ранее в работах [13–15], которая основана на использовании безразмерных критериев для нахождения искомых параметров. Математически задача сводится к решению уравнения Фурье с соответствующими граничными условиями (1)–(2), из которого находится значение теплового потока на границе зоны оттаивании мерзлых пород.
Постановка задачи в безразмерном виде
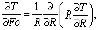1 ≤ R ≤ S (1)
T = to, R = 1. (2)
Исходным выражением для получения расчетных формул является условие Стефана, которое для однофазной задачи может быть записано в следующем безразмерном виде
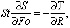T = T0. R = S. (3)
В выражениях (1)–(3) приняты следующие безразмерные переменные:
R = r/Ro; T = Tр/Te; to = t/ Te;
S = Sh/R0; Sh = h + R0.
Так как горные выработки подземных сооружений редко имеют классическую круговую (цилиндрическую) симметрию, для их приведения к канонической форме воспользуемся понятием «эквивалентного радиуса», который определяется по простой формуле [1,15]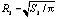 
. Где S0 – реальное сечение горной выработки любой формы, м2. В таблице приведены значения эквивалентного радиуса для выработок различных сечений, характерных для подземных сооружений криолитозоны.
Соответствие сечения выработки эквивалентному радиусу
|
S0, м2 |
7,0 |
10,0 |
12,0 |
15,0 |
20,0 |
30,0 |
40,0 |
50,0 |
|
R0, м |
1,5 |
1,8 |
2,0 |
2,2 |
2,5 |
3,1 |
3,6 |
4,0 |
Остальные обозначения в формулах (1)–(3): Fo – число (критерий) Фурье, равное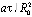 
, где a – температуропроводность горных пород, м2/с. Температуропроводность горных пород (коэффициент температуропроводности) является комплексной величиной, определяется по формуле: a = ƛ/(сρ), где с – удельная теплоемкость горных пород, Дж/кг∙К; ρ – плотность горных пород, кг/м3; ƛ – коэффициент теплопроводности горных пород, Вт/(м К). St – число (критерий) Стефана, равное Lw/ct, где L – скрытая теплота плавления льда, Дж/(кг К); w – льдистость горных пород, д.е.; t – температура воздуха в период оттаивания, °С; R0 –характерный размер, который в данном случае примем равным эквивалентному радиусу, м; h – глубина оттаивания пород, м; r – координата, м.
Используя допущение о том, что профиль изменения температуры в талой зоне аналогичен стационарному профилю температуры в пределах талой зоны пород, в работе [1] было получено выражение для определения длительности периода оттаивания горных пород на заданную глубину, которое в безразмерном виде можно записать в компактной форме:
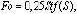(4)
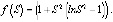(5)
Данное уравнение является трансцендентным. То есть недостатком этого выражения является невозможность в явном виде выразить зависимость безразмерной глубины оттаивания пород от времени (критерия Фурье). В связи с этим путем аппроксимации функции (5) нами было получено простое выражение для определения параметра «S» в зависимости от значения чисел Fo и St.
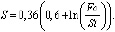(6)
Выражение (6) действительно при выполнении условия (Fo/St) ≥ 0,16. Это соответствует значению безразмерной глубины оттаивания S ≥ 1,5. То есть выражение (4) для определения длительности периода оттаивания горных пород вокруг выработок подземного сооружения (при выполнении данного условия) с достаточной для инженерных расчетов точностью, может быть записано в виде
Fo = 0.0025St(exp(2,775S)). (7)
Результаты исследования и их обсуждение
Диапазон изменения, который ограничивает применение упрощенной формулы, был обоснован анализом характерных условий эксплуатации капитальных подземных сооружений криолитозоны, эксплуатирующихся с естественным (нерегулируемым) тепловым режимом, либо с положительным тепловым режимом. В первом случае критерий Фурье, как правило, больше 3. А во втором – больше 10. Поскольку число Стефана для горных пород криолитозоны, как правило, не превышает 15, то минимальное соотношение (Fo/St) не будет ниже значения 0,2. Таким образом, определенная с запасом граница (Fo/St) ≥ 0,16 является достаточно надежным условием применения упрощенной расчетной формулы (7). По полученным формулам были проведены вариантные расчеты, которые представлены в виде графиков на рисунках 1–4. На рис. 1 показана зависимость критерия Фурье от безразмерного радуса оттаивания горных пород вокруг выработки подземного сооружения, вычисленного по формуле (7) – кривая 1 и формуле (5) – кривая 2 для различных значений числа Стефана.
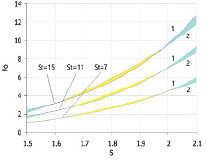
Рис. 1. Изменение числа Фурье в зависимости от безразмерного радиуса оттаивания пород при различных значениях числа Стефана: 1 – формула (7); 2 – формула (5)
Голубым цветом на рисунке выделены участки, где значения числа Фурье, определенные по формуле (7), больше, чем вычисленные по формуле (5). Желтым цветом – наоборот. Суммарная площадь участков различного цвета приблизительно одинакова. Как видно из рисунка, в рассматриваемом диапазоне изменения значений безразмерного радиуса оттаивания пород обе формулы дают приблизительно одинаковый результат в широком диапазоне изменений чисел Стефана (от 7 до 15). Что охватывает практически весь возможный диапазон климатических и геокриологических условий эксплуатации подземных сооружений в криолитозоне [7, 14, 15].
Для наглядности и сравнения на рис. 2 приведен 3D график, охватывающий диапазон изменения параметра S от 1 до 2 и числа Стефана от 5 до 15.
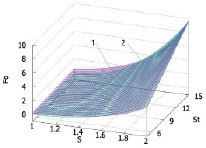
Рис. 2. Изменение числа Фурье в зависимости от числа Стефана при различных значениях безразмерного радиуса оттаивания пород: 1 – формула (7); 2 – формула (5)
Как видно из графиков, на участке изменения параметра S от 1 до 1,5 плоскости расходятся. А на участке, где S больше значения 1,5, практически сливаются. Это свидетельствует о неплохой точности результатов при использовании аппроксимирующей функции (7) в данном диапазоне для значений числа Стефана во всем возможном на практике интервале изменения от 5 до 15. Само понятие «неплохой точности» является условным. В технических науках принят не качественный, а количественный критерий оценки точности. Обычно считается, что достаточной для инженерных расчетов точностью является ошибка, не превышающая 10 % от значения искомой величины. В связи с этим была сделана количественная оценка точности расчетов при замене уравнения (5) на уравнение (7). На рис. 3 приведен график, характеризующий изменение относительной ошибки в диапазоне изменения безразмерного радиуса оттаивания от 1 до 2.
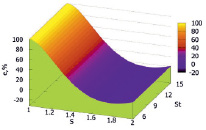
Рис. 3. Относительная ошибка в расчетах критерия Фурье при замене формулы (5) на формулу (7) при 1 ≤ S ≤ 2
Из графика видно, что, чем меньше значение безразмерного радиуса оттаивания, тем относительная ошибка больше. Причем, как и следовало ожидать (это видно из простого сравнения расчетных формул), относительная ошибка не зависит от критерия Стефана: кривые на графике при St = 5 и St = 15 идентичны. В то же время из графика следует, что существует область (выделена синим цветом), где ошибка меньше допустимой в инженерной практике. Для наглядности эта область представлена отдельно на рис. 4.
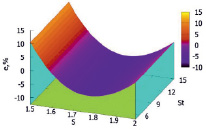
Рис. 4. Относительная ошибка в расчетах критерия Фурье при замене формулы (5) на формулу (7) при 2 ≥ S ≥ 1,5
На рисунке отчетливо видно, что для случая, когда безразмерный радиус оттаивания изменяется в диапазоне 2 ≥ S ≥ 1,5, относительная ошибка не превышает допустимого в инженерной практике значения. То есть применение формулы (7) для прогноза глубины оттаивания пород является допустимым в указанной области изменения исходных параметров: критерия Фурье и безразмерного радиуса.
Заключение
Обоснована актуальность исследований, направленных на прогноз и управление температурным режимом мерзлых пород вокруг подземных сооружений криолитозоны, эксплуатирующихся при положительном тепловом режиме, допускающем оттаивание горных пород на заданную глубину. Сформулирована и записана задача, подлежащая решению в безразмерном (критериальном) виде. Путем аппроксимации функции из известного решения однофазной задачи Стефана при граничных условиях первого рода для объектов цилиндрической симметрии получено выражение для определения безразмерного радиуса оттаивания в зависимости от критериев Фурье и Био. Проведено сравнение результатов расчетов по исходной и приближенной формулам в широком диапазоне изменения начальных данных, характерных для условий эксплуатации подземных сооружений криолитозоны. Установлено, что относительная ошибка расчетов не зависит от критерия Стефана и является только функцией критерия Фурье. Определена область возможного использования приближенной формулы, в которой относительная ошибка не превысит допустимой в инженерной практике величины. Показано, что для большинства практически интересных случаев возникающая при прогнозе глубины оттаивания ошибка может быть отнесена в расчетный запас.
Дальнейшие исследования в данной области должны быть направлены на получение простой формулы прогноза глубины оттаивания пород вокруг выработок цилиндрической и сферической симметрии для подземных сооружений криолитозоны с небольшим сроком эксплуатации. Необходимо также провести сравнение использованных аналитических формул с результатами численного моделирования соответствующих типовых теплофизических задач с помощью существующих программных комплексов.