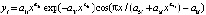Мы выдвинули доктрину колебательной адаптации в природе, включая живое и косное вещества по В.И. Вернадскому [1]. Тогда получается, что закон Коммонера «всё связано со всем» [2] исходит из взаимных колебаний процессов адаптации, которые проявляются в виде суммы асимметричных вейвлет-сигналов (уединенных волн).
Урбанизация оказывает существенное влияние на климат и метеорологические условия. Данные были собраны на 15 уровнях на 325-метровой метеорологической башне в Пекине в 1991–2011 гг. Ежегодная и сезонная (весна, лето, осень и зима) средняя скорость ветра на 15 уровнях имеет тенденции снижения. Заметен феномен «излома» в профиле ветра, и средняя высота излома увеличилась примерно от 40 до почти 80 м [3].
Мы рассматриваем урбанизацию как географическое стягивание всех параметров жизни населения к центрам столиц субъектов Федераций России. Фактически всё население стремится к столицам, повышая численность городского населения.
Наземные растения вместе с океаном обеспечили обитаемость жизни на планете. Однако использование ископаемого топлива к середине XXI в. даст объемы CО2, сравнимые с ранним эоценом (примерно 50 млн лет назад). Если концентрация CО2 будет нарастать такими же темпами и в XXIII в., то уже планета Земля будет вести себя так же, как 1,5 млрд лет назад [4]. В итоге будущее программы снижения количества СО2 имеется в увеличении на поверхности суши лесов [5]. Тогда к центрам столиц субъектов также можно стягивать любые параметры окружающей и природной среды, включая климат и погоду.
Цель исследования – выявление ранговых распределений 40 параметров для рейтинга субъектов региона, вейвлет-анализ парных взаимодействий, суммирование коэффициентов корреляции по строкам и столбцам корреляционной матрицы и составление рейтингов влияющих переменных и зависимых показателей. Метод применим для сравнения жизни населения субъектов по множеству параметров, привязанных к центрам столиц субъектов.
Материалы и методы исследования
Нами составлены консолидированные данные относительно географических параметров (широта, долгота, высота) для центров столиц у субъектов федерации, 13 видов угодий из кадастра, экологических и экономических показателей [1] (табл. 1).
Таблица 1
Фрагмент данных по 40 параметрам у 14 субъектов Урала и Сибири
|
Код |
Субъект федерации Урала и Сибири |
Столица субъекта |
Координаты |
||||
|
Х01 |
Х02 |
Х03 |
… |
Х40 |
|||
|
45 |
Курганская область |
Курган |
5.45 |
5.3333 |
75 |
… |
262.2 |
|
66 |
Свердловская область |
Екатеринбург |
6.8519 |
0.6122 |
255 |
… |
251.9 |
|
72 |
Тюменская область |
Тюмень |
7.1522 |
5.5272 |
81 |
… |
174.1 |
|
74 |
Челябинская область |
Челябинск |
5.154 |
1.4291 |
218 |
… |
251.0 |
|
4 |
Республика Алтай |
Горно-Алтайск |
1.9606 |
25.9189 |
285 |
… |
222.3 |
|
17 |
Республика Тыва |
Кызыл |
1.7147 |
34.4534 |
624 |
… |
378.1 |
|
19 |
Республика Хакасия |
Абакан |
3.7156 |
31.4292 |
247 |
… |
249.9 |
|
22 |
Алтайский край |
Барнаул |
3.3606 |
23.7636 |
189 |
… |
260.1 |
|
24 |
Красноярский край |
Красноярск |
6.0184 |
32.8672 |
139 |
… |
262.1 |
|
38 |
Иркутская область |
Иркутск |
2.2978 |
44.296 |
427 |
… |
320.1 |
|
42 |
Кемеровская обл. – Кузбасс |
Кемерово |
5.3333 |
26.0833 |
104 |
… |
342.8 |
|
54 |
Новосибирская область |
Новосибирск |
5.0415 |
22.9346 |
164 |
… |
232.1 |
|
55 |
Омская область |
Омск |
4.9924 |
13.3686 |
90 |
… |
220.3 |
|
70 |
Томская область |
Томск |
6.4977 |
24.9744 |
117 |
… |
201.3 |
Параметры распределились по следующим группам: 1) координаты центров столиц субъектов (Х01 – северная широта, 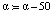 , 0; Х02 – восточная долгота,
, 0; Х02 – восточная долгота, 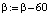 , 0; Х03 – высота над Балтийским морем, м); 2) климатические (среднемесячные) параметры за период 1961–1990 гг. (Х04 – ночная температура, °С; Х05 – дневная температура, °С; Х06 – сумма осадков, мм; Х07 – число дней с осадками более 0,1 мм, шт.); 3) погода за 2018 г. (Х08 – январская средняя температура, °С; Х09 – июльская средняя температура, °С; Х10 – сумма осадков за январь, мм; Х11 – сумма осадков за июль, мм); 4) доли ( %) угодий к суше (Х12 – доля сельхозугодий; Х13 – доля лесов; Х14 – для пашни; Х15 – доля растительности «трава + кусты + деревья»; Х16 – антропогенные угодья; Х17 – экологический коэффициент, вычисляемый делением растительности к площади измененных угодьям); 5) удельные потребление воды, сброс и выброс загрязнений (Х18 – забор воды, м3/чел.; Х19 – использование воды, м3/чел.; Х20 – сброс загрязнений, м3/чел.; Х21 – выбросы в атмосферу, кг/чел.; Х22 – улавливание загрязняющих веществ из выбросов, кг/чел.); 6) параметры людей (Х23 – плотность населения, чел/км2; продолжительность жизни (ожидаемая), лет: Х24 – всех людей; Х25 – мужского населения; Х26 – женского населения); 7) демографические показатели (Х27 – коэффициент рождаемости (суммарный); Х28 – смертность младенцев на 1000 родившихся живыми; Х29 – коэффициент миграционного прироста на 10 тыс. населения; Х30 – естественный прирост на тысячу населения); 8) параметры труда (Х31 – занятость, %; Х32 – безработица, %; Х33 – доля населения, находящегося ниже прожиточного минимума, %; Х34 – городское население, %; Х35 – сельское население, %); 9) экономика производственных процессов (Х36 – ВРП за 2018 г. на душу населения, тыс. руб/чел.; Х37 – душевые доходы, руб/ мес.; умершие в трудоспособном возрасте на 105 населения, чел.: Х38 – обоих полов; Х39 – мужчин в возрасте 16–59 лет; Х40 – женщин в возрасте 16–54 года).
, 0; Х03 – высота над Балтийским морем, м); 2) климатические (среднемесячные) параметры за период 1961–1990 гг. (Х04 – ночная температура, °С; Х05 – дневная температура, °С; Х06 – сумма осадков, мм; Х07 – число дней с осадками более 0,1 мм, шт.); 3) погода за 2018 г. (Х08 – январская средняя температура, °С; Х09 – июльская средняя температура, °С; Х10 – сумма осадков за январь, мм; Х11 – сумма осадков за июль, мм); 4) доли ( %) угодий к суше (Х12 – доля сельхозугодий; Х13 – доля лесов; Х14 – для пашни; Х15 – доля растительности «трава + кусты + деревья»; Х16 – антропогенные угодья; Х17 – экологический коэффициент, вычисляемый делением растительности к площади измененных угодьям); 5) удельные потребление воды, сброс и выброс загрязнений (Х18 – забор воды, м3/чел.; Х19 – использование воды, м3/чел.; Х20 – сброс загрязнений, м3/чел.; Х21 – выбросы в атмосферу, кг/чел.; Х22 – улавливание загрязняющих веществ из выбросов, кг/чел.); 6) параметры людей (Х23 – плотность населения, чел/км2; продолжительность жизни (ожидаемая), лет: Х24 – всех людей; Х25 – мужского населения; Х26 – женского населения); 7) демографические показатели (Х27 – коэффициент рождаемости (суммарный); Х28 – смертность младенцев на 1000 родившихся живыми; Х29 – коэффициент миграционного прироста на 10 тыс. населения; Х30 – естественный прирост на тысячу населения); 8) параметры труда (Х31 – занятость, %; Х32 – безработица, %; Х33 – доля населения, находящегося ниже прожиточного минимума, %; Х34 – городское население, %; Х35 – сельское население, %); 9) экономика производственных процессов (Х36 – ВРП за 2018 г. на душу населения, тыс. руб/чел.; Х37 – душевые доходы, руб/ мес.; умершие в трудоспособном возрасте на 105 населения, чел.: Х38 – обоих полов; Х39 – мужчин в возрасте 16–59 лет; Х40 – женщин в возрасте 16–54 года).
Вейвлет-сигналы как асимметричные колебания имеют вид формулы
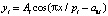 ,
,
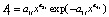 ,
,
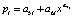 , (1)
, (1)
где y – зависимый показатель, i – номер члена модели (1), x – влияющая переменная, a1...a8 – параметры уравнения (1), идентифицируемые при идентификации в программной среде CurveExpert-1.40; Ai – амплитуда (половина) колебания, pi – полупериод колебания.
Ранжирование значений параметров субъектов федерации
Иерархия показывает в системе параметров упорядоченность, поэтому является некоторой абстракцией структуры системы, предназначенной для изучения функциональных взаимодействий между ее компонентами и их функциональных воздействий на систему в целом [6]. Метод анализа иерархий Саати получил в мировой науке широкое распространение.
Синтез иерархического распределения возможен двумя способами, причем для известной или составленной (в нашем примере данной статьи) системы параметров:
1) вначале необходимо упорядочение значений параметров по заранее установленному вектору предпорядка предпочтительности «лучше → хуже» по последовательности рангов R = 0, 1, 2,..., после этого суммирование рангов по всему ранжированному списку параметров; в итоге образуется рейтинг элементов системы (в нашем примере 14 субъектов Урала и Сибири), причем лучшим будет элемент (субъект Федерации) с наименьшей суммой рангов;
2) как и в методе Саати [6], выполняется парное сравнение параметров системы, методом идентификации выявляются закономерности бинарных отношений между всеми параметрами, затем коэффициенты корреляции по строкам и столбцам суммируются, после этого выявляются рейтинги параметров как влияющих переменных и зависимых показателей.
Приведем рейтинг системы факторов (табл. 2) по сумме рангов.
Таблица 2
Фрагмент ранжирования параметров субъектов Федерации
|
Код |
Координаты |
Климат |
Рейтинг |
Модель (2) |
||||||||||
|
01 |
02 |
03 |
04 |
05 |
06 |
07 |
… |
39 |
40 |
I |
ΣR |
ε |
Δ, % |
|
|
45 |
9 |
2 |
0 |
3 |
2 |
11 |
10 |
… |
10 |
10 |
12 |
300 |
-7.87644 |
-2.63 |
|
66 |
12 |
0 |
10 |
0 |
4 |
2 |
4 |
… |
7 |
7 |
3 |
220 |
4.66642 |
2.12 |
|
72 |
13 |
3 |
1 |
5 |
6 |
4 |
5 |
… |
0 |
0 |
1 |
171 |
6.15217 |
3.60 |
|
74 |
7 |
1 |
8 |
2 |
1 |
7 |
8 |
… |
4 |
6 |
9 |
289 |
5.41382 |
1.87 |
|
4 |
1 |
8 |
11 |
10 |
8 |
1 |
0 |
… |
6 |
3 |
4 |
222 |
1.0128 |
0.46 |
|
17 |
0 |
12 |
13 |
12 |
11 |
12 |
13 |
… |
11 |
13 |
11 |
297 |
-4.03939 |
-1.36 |
|
19 |
4 |
10 |
9 |
13 |
13 |
13 |
12 |
… |
9 |
5 |
8 |
279 |
6.2439 |
2.24 |
|
22 |
3 |
6 |
7 |
4 |
0 |
8 |
6 |
… |
7 |
8 |
13 |
312 |
-1.56 |
-0.50 |
|
24 |
10 |
11 |
5 |
7 |
9 |
3 |
3 |
… |
5 |
9 |
6 |
243 |
-3.10485 |
-1.28 |
|
38 |
2 |
13 |
12 |
11 |
7 |
4 |
11 |
… |
12 |
11 |
10 |
292 |
-0.97374 |
-0.33 |
|
42 |
8 |
9 |
3 |
9 |
10 |
6 |
2 |
… |
13 |
12 |
14 |
324 |
5.84706 |
1.80 |
|
54 |
6 |
5 |
6 |
1 |
3 |
9 |
7 |
… |
2 |
4 |
5 |
224 |
-7.1391 |
-3.19 |
|
55 |
5 |
4 |
2 |
6 |
5 |
10 |
8 |
… |
3 |
2 |
7 |
266 |
5.67882 |
2.13 |
|
70 |
11 |
7 |
4 |
8 |
12 |
0 |
1 |
… |
1 |
1 |
2 |
190 |
-9.95284 |
-5.24 |
Примечание. Максимальная относительная погрешность равна 5,24 %; полужирным выделены субъекты Ангаро-Енисейского макрорегиона.
Ранг 0 – если больше, то лучше (или знак ↑): Х04 – Х11, Х13, Х15, Х17, Х24 – Х27, Х29 – Х31, Х35 – Х37. Ранг 1 – если меньше, то лучше (или знак ↓): Х01 – Х03, Х12, Х14, Х16, Х18 – Х23, Х28, Х32 – Х34, Х38 – Х40. В функции Excel =РАНГ(C2;C$2:C$16;1) принимаются следующие условные обозначения: C – идентификатор (обозначение) ранжируемого столбца; С2, C$2 – первая строка ряда; C$16 – последняя строка ряда; 0 1 – ранжирование происходит по убыванию (0) или возрастанию (1). Это дает место I, а ранг равен R = I – 1.
1 – ранжирование происходит по убыванию (0) или возрастанию (1). Это дает место I, а ранг равен R = I – 1.
Из табл. 2 видно, что первое место с суммой рангов 171 занял субъект федерации с кодом 72 (Тюменская область). Сравнение показывает, что лучшее теоретическое первое место получится, если ΣR = 0. Тогда у Тюменской области имеются резервы повышения эффективности деятельности. На втором месте с суммой рангов 190 находится Томская область. А на третьем месте с суммой 220 – Свердловская область.
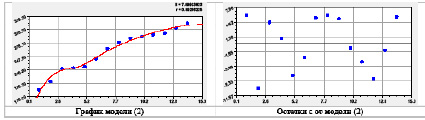
Рис. 1. Графики влияния места на сумму рангов в рейтинге субъектов (в правом верхнем углу показано: S – стандартное отклонение; r – коэффициент корреляции)
После идентификации формулы (1) получена (рис. 1) закономерность
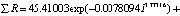
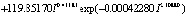 , (2)
, (2)
где ΣR – сумма рангов по 40 параметрам 14 субъектов федерации, I – место в рейтинге. Остатки ε получаются вычитанием из фактических значений уф суммы рангов расчетных значений y по (2). Относительная погрешность ошибки моделирования Δ = 100ε/уф, %.
Коэффициент корреляции является мерой адекватности формулы (2), и он равен 0,9926. Он выше уровня 0,95 «сверхсильная факторная связь».
Из точечного графика остатков на рис. 1 видно, что значения параметров (ордината) изменяются по местам (или рангам) абсциссы волнообразно. В связи с этим тренд (2) можно будет дополнять колебаниями. Причем амплитуда волн будет зависеть от количества субъектов федерации. Будем считать, что идентификация (1) потребуется только при превышении ошибки моделирования более 5 %. Поэтому у всех 40 параметров для всех субъектов России (82 шт.) тренды (2) нужно будет дополнять асимметричными волновыми уравнениями (1).
Корреляционная матрица, рейтинг факторов
Итоги процесса идентификации трендом (частный случай асимметричного вейвлета) распределений по рангам (в диагональных клетках) и парных отношений между 40 факторами приведены в табл. 3.
Таблица 3
Корреляционная матрица (по трендам) и рейтинг факторов (фрагмент)
|
Переменные x |
Зависимые от переменных факторы (показатели y) |
Сумма Σr |
Место Ix |
||||
|
Х01 |
Х02 |
… |
Х39 |
Х40 |
|||
|
Х01 |
0,9954 |
0,6373 |
… |
0,6875 |
0,5950 |
27,6456 |
2 |
|
Х02 |
0,6526 |
0,9755 |
… |
0,5389 |
0,6407 |
22,4040 |
16 |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
Х39 |
0,6176 |
0,4087 |
… |
0,9808 |
0,8925 |
20,7444 |
24 |
|
Х40 |
0,5379 |
0,5005 |
… |
0,9469 |
0,9870 |
24,6787 |
10 |
|
Сумма Σr |
24,0392 |
21,6472 |
… |
21,0033 |
22,8498 |
881,529 |
– |
|
Место Iy |
11 |
22 |
… |
26 |
16 |
– |
0,5551 |
Коэффициент коррелятивной вариации (определяется по Чарльзу Дарвину) по табл. 3 будет равным 881,529 / 402 = 0,5551, что дает средний уровень адекватности (0,5–0,7).
Как влияющая переменная на первом месте располагается фактор Х19 – использование извлеченной воды, на втором – Х01 – северная широта, на третьем – Х32 – уровень безработицы среди населения. Как зависимый показатель (то есть критерий оценки) на первом месте находится параметр Х33 – доля населения ниже прожиточного минимума, на втором – Х26 – ожидаемая продолжительность жизни женщин, на третьем – Х32 – уровень безработицы.
Закономерности распределений сумм коэффициентов корреляции по местам по модели (1) приведены в табл. 4 (рис. 2 и 3).
Таблица 4
Параметры модели (1) влияния мест на суммы рангов
|
Номер i |
Асимметричный вейвлет |
Коэф. корр. r |
|||||||
|
Половина амплитуды колебания |
Половина периода колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
Рейтинг 40 параметров субъектов СФО как влияющих переменных |
|||||||||
|
1 |
573,635 |
0 |
0,0003284 |
1 |
0 |
0 |
0 |
0 |
0,9961 |
|
2 |
-485,0072 |
0,00232 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
0,0018445 |
0 |
-2,71813 |
0,22812 |
17,38416 |
-0,0002256 |
2,74656 |
0,98491 |
|
|
4 |
581,479 |
0 |
6,96526 |
0,05472 |
6,00598 |
-0,098248 |
0,77973 |
-0,7915 |
0,5219 |
|
5 |
-0,25716 |
1,15875 |
2,11273 |
0,22414 |
11,18558 |
-0,0012335 |
2,26572 |
-0,7370 |
0,3809 |
|
6 |
-1,8525e8 |
4,79888 |
20,80579 |
0,17713 |
-3,74001 |
5,21415 |
0,06832 |
5,35332 |
0,7243 |
|
Рейтинг 40 параметров субъектов СФО как зависимых показателей |
|||||||||
|
1 |
29,60095 |
0 |
-0,0057240 |
1 |
0 |
0 |
0 |
0 |
0,9972 |
|
2 |
-1,81452 |
0,59914 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
-0,27012 |
0 |
-0,0003657 |
2,49704 |
1,27119 |
0,049148 |
1,31692 |
5,08767 |
|
|
4 |
-0,10900 |
0 |
0,016377 |
1 |
5,31115 |
0,35185 |
0,60081 |
-0,2597 |
0,2575 |
|
5 |
1,206e-14 |
9,95647 |
0,11670 |
1,01327 |
49,01669 |
-1,02649 |
1,00047 |
-1,3851 |
0,7683 |
|
6 |
-1,097e-16 |
17,5158 |
0,84714 |
1,00348 |
4,50414 |
-0,0032434 |
1,02041 |
4,91380 |
0,6119 |
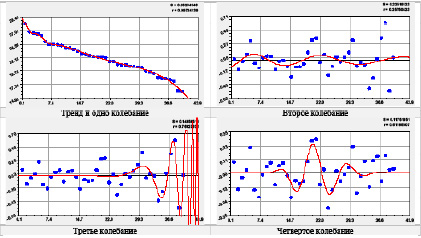
Рис. 2. Распределения сумм коэффициентов корреляции показателей
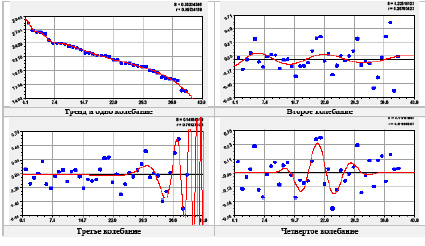
Рис. 3. Графики распределения сумм коэффициентов корреляции показателей
Наиболее опасным становится третье колебание из рис. 2, который показывает рост амплитуды и частоты колебания.
Первый член у обоих рейтингов является законом Мандельброта (в физике), поэтому колебания располагаются как некратные фракталы. Это же выражение называется законом Лапласа (известно в математике), Перла – Ципфа (в науке биология) и Парето (применяется в эконометрике). Видно, что поведение субъектов происходит по экспоненциальному закону спада для всех 40 параметров как влияющих переменных. Однако по первому члену в виде экспоненциального роста происходит изменение 40 факторов как зависимых показателей.
В обоих случаях по второму члену в виде степенной функции происходит кризис (отрицательный знак) в рейтинге 40 параметров. Последующие кванты поведения для рейтинга показателей имеют кризисный характер и вейвлетов № 3, 4 и 6. Это происходит из-за слабого осознания людьми (специалистами) взаимных парных связей между факторами.
Наиболее опасным становится третье колебание из рис. 3, которое показывает рост амплитуды и частоты колебания.
Вейвлет по формуле (1) становится универсальной уединенной волной, поэтому он будет определять так называемый квант поведения. Поэтому, в отличие от квантовой механики микромира, где рассматриваются в основном кванты структуры, нами предлагаются для поведения природных и природно-антропогенных объектов кванты функционирования. Причем совокупность квантов поведения необходима в природе для колебательной адаптации.
Заключение
Составлены интегрированные данные по 40 параметрам для 14 субъектов из Уральского и Сибирского федеральных округов относительно географических координат (широты, долготы и высоты) центров их столиц, видов угодий из земельного кадастра, экологических и многих социально-экономических показателей.
Коэффициент коррелятивной вариации всей матрицы по столбцам и строкам из 40 параметров получился равным 0,5551, и это значение относится к среднему уровню адекватности. По этому критерию можно сравнивать разнородные объекты исследования. Сравнение объектов выполняется по функциональной связности между учтенными в системе параметрами.
В ранжировании субъектов первое место с суммой рангов 171 заняла Тюменская область. На втором месте с суммой рангов 190 находится Томская область. А на третьем месте с суммой 220 – Свердловская область.
Среди влияющих переменных на первом месте расположился фактор Х19 – использование извлеченной воды, на втором фактор Х01 – северная широта, на третьем – Х32 – уровень безработицы. Среди зависимых показателей на первом месте находится параметр Х33 – доля населения ниже прожиточного минимума, на втором – Х26 – ожидаемая продолжительность жизни женщин, на третьем – Х32 – уровень безработицы.
Результаты применимы для сравнения разных множеств субъектов (от федеральных округов до муниципалитетов) в целом по Российской Федерации. На первые места в рейтингах выходят жизненно важные показатели для людей.