Для исследования формы и асимметрии органов и частей организмов широко используется метод геометрической морфометрии, особенность которого – в измерении расстояний в прокрустовом (усредненном) пространстве. В подобных исследованиях важной является репрезентативность получаемых результатов, т.е. возможность получить сходный результат при повторном сборе материала через промежуток времени. Вопрос о мнимых и настоящих повторностях широко дискутировался в работах зарубежных и отечественных ученых [1; 2]. Итог дискуссии – строгий подход к повторным измерениям и тщательное описание методики подготовки выборочного экспериментального и контрольного материала.
В отличие от сельскохозяйственных методов сбора с нескольких делянок, в предыдущих работах нами предлагался троекратный сбор с одной делянки, что может восприниматься критически, учитывая неоднородность ландшафта или пестроту почвенных горизонтов [3]. При определении разных видов асимметрии точность измерения повышается как при повторном измерении, так и при увеличении объема выборки, например это продемонстрировано в работе с листовыми пластинами березы повислой (Betula pendula Roth.) при тестировании флуктуирующей асимметрии линейным методом [4]. Замечено, что индивидуальный подход исследователя играет также важную роль – воспроизводимость результатов, полученных разными лицами, была крайне низка при работе с одним гербарным материалом [5]. Таким образом, точность измерения зависит от многих методологических нюансов, влияющих на репрезентативность результатов.
В нашей работе под листовой пластиной мы подразумевали мнимую повторность, полагая, что это имеет лишь теоретический смысл, поскольку лист уникален, за исключением гомогенных гаметных особей, например происходящих от одного растения, которые генетически однородны, но развиваются и функционируют в неповторимых условиях освещенности. Промежуток между сборами нами сокращался до минимума (3-4 часа), и в течение одного дня сбор проводился в три подхода к каждой делянке. Учитывался опушечный эффект, т.е. не собирались листья с границы участка – полосы шириной 1 м. Площадь делянки составляла 35 м2, что позволяло собирать равномерно листовые пластины без учета количества листьев с одного растения, главное условие – одинаковая длина листовых пластин.
В отличие от образцов с жестким скелетом, листовая пластина крайне неоднородна по длине, ширине и форме, поэтому ошибка в размере центроида (усредненного консенсуса) бывает очень велика. Влияет ли изменчивость листьев на ошибку измерения асимметрии и в конечном счете на ее величину? Между ошибкой, вызванной изменчивостью величины центроида, и ошибкой, возникающей при определении асимметрии в прокрустовом дисперсионном анализе, нет строгой корреляции. Другими словами, асимметричным может быть как крупный лист, так и лист среднего или малого размера. Вместе с тем известно, что статистически значимая величина флуктуирующей асимметрии (ФА) связана с ошибкой в прокрустовом дисперсионном анализе обратной зависимостью. Если ФА существует в смеси с направленной асимметрией (НА), то ошибка не коррелирует с величиной флуктуирующей асимметрии. Влияние рандомной и систематической ошибки на результат прокрустова анализа рассматривалось в основном в антропологических и зоологических исследованиях [6-8]. Число степеней свободы, как правило, зависит от числа расставляемых меток или полуметок, а ошибка включает погрешности, вызванные повторным нанесением меток и повторным фотографированием или сканированием. Повышение числа степеней свободы при увеличении повторностей измерения приводило к существенному снижению ошибки [9; 10].
Под рандомной ошибкой мы подразумевали ошибку, вызванную сбором листовых пластин с различающимися геометрическими характеристиками. В то же время известно, что метод геометрической морфометрии нивелирует гетерогенность формы, следовательно, ожидаемо, что влияние формы на асимметрию будет незначительно.
В настоящей работе мы под систематической ошибкой подразумевали необъясненную дисперсию, возникавшую при повторных измерениях и связанную: а) с ошибками фотографирования и нанесения меток; б) ошибками при использовании разного числа наносимых меток; в) ошибками при использовании разного числа образцов в выборке. В предыдущей работе ошибка, вызванная повторным фотографированием, была ничтожно мала [3].
Увеличение числа меток для большей точности измерения может повышать ошибку и быть бесполезным для оценки формы и асимметрии [11]. В предыдущих работах расстановка 25 меток проводилась по обеим сторонам листовой пластины, выравнивалась форма образцов и выполнялся прокрустов дисперсионный анализ, т.е. определялись статистически значимые различия дисперсии левых и правых меток в зависимости от дозы удобрения и методов предпосевной обработки почвы [12].
Цель исследования – нахождение оптимального числа меток для определения асимметрии в прокрустовом анализе и оптимального числа образцов в выборке, когда дальнейшее их увеличение уже не влияет на статистическую значимость, т.е. изучение влияния систематических ошибок на статистическую значимость билатеральной асимметрии.
Материалы и методы исследования
Для исследования были выбраны образцы листовых пластин озимой пшеницы (Triticum aestivum L., сорт Поэма), выращенной с использованием четырех разных составов минеральных удобрений в 2019-2021 гг. Использовались флаговые листовые пластины длиной 12-16 см без механических повреждений, включая повреждения, вызванные болезнями или насекомыми-фитофагами. Листовые пластины обладали асимметричными свойствами в виде смеси флуктуирующей и направленной асимметрии.
Методы сбора, оцифровывания, нанесения меток и алгоритм проведения анализа формы и асимметрии подробно описаны в предыдущей работе [3]. Систематическая ошибка тестирования асимметрии в прокрустовом дисперсионном анализе определялась по величине MS остатков и сравнивалась с помощью регрессии с показателями F Гудолла ФА и НА. Для получения регрессии проводилось моделирование значений ошибки и показателей F Гудолла. За отправные значения брались 4 величины, полученные в прокрустовом анализе. По стандартному отклонению и значению среднего арифметического генерировалось 100 значений с нормальным распределением (горизонтальная ось на рисунках). При моделировании ошибки использовались результаты прокрустова анализа с числом образцов: 25, 50, 100 и с числом меток: 24, 50 и 100 с четным количеством на каждой стороне листовой пластины, за исключением двух меток, лежавших на оси симметрии, в основании и на верхушке листа. Оценка полученных трендовых зависимостей в порядке возрастания проводилась по коэффициентам регрессии, а сами ряды значений сравнивались в однофакторном дисперсионном анализе.
Результаты исследования и их обсуждение
Кривые регрессии получены на основе аргументов n, расположенных в порядке возрастания значений (рис. 1 и 2). Это позволило найти различие ошибки и ее тенденцию к росту по углу наклона кривой, представленной в виде логарифмической линии тренда с коэффициентом детерминации R2 = 0,83-0,93. Заметим, что линии тренда не несли смысла корреляционной зависимости, а показывали лишь степень регрессии.
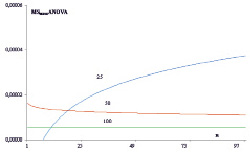
Систематическая ошибка в прокрустовом дисперсионном анализе. Прокрустов дисперсионный анализ показывает значимость отклонения координат парных меток относительно оси симметрии. Увеличение числа образцов в выборке до 100 приводило к существенному снижению величины ошибки MSerror ANOVA (рис. 1).
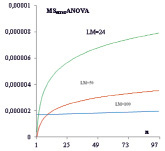
При использовании 100 образцов листьев ошибка снижалась на 44,4 % от ошибки, полученной при объеме выборки, равной 25, и на 23,5 % от ошибки для выборки с числом листовых пластин, равным 50. Статистическая значимость прокрустова анализа оставалась высокой для всех объемов выборки (р << 0.0001), при этом линии тренда существенно отличались (F = 93.75). При увеличении числа меток до 100 ошибка была близка к постоянной, при числе наносимых меток LM = 24 MSerrоrANOVA – увеличивалась на 28-30 %. Статистическая значимость направленной и флуктуирующей асимметрии сохранялась на прежнем уровне, межгрупповые различия (F) между рядами генерируемых значений оставались высокими (p << 0.001).
Влияние числа меток на изменчивость флуктуирующей и направленной асимметрии. Основная задача методов геометрической морфометрии – тестирование изменчивости формы и асимметрии. Принято считать, что ошибка зависит от дисперсии значений, которая связана в свою очередь с погрешностью измерения.
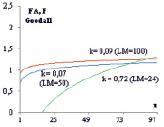
Мы исследовали влияние числа меток в выборке на изменчивость ФА и НА с помощью критерия F Гудолла. Использовалась выборка из 100 образцов, обладавшая высокой НА и ФА (соответственно, F = 14,3; F = 1,18; p << 0.0001). Как и ожидалось, при числе меток LM = 50-100 отмечалась наименьшая дисперсия в ряду сгенерированных значений. Коэффициенты регрессии были меньше (k = 0,09 и k = 0,07) по сравнению с числом меток, равным 24 (k = 0,72) (рис. 2).
А Б
Рис. 1. Зависимость ошибки измерения (MSerrorANOVA) от числа образцов (А) и меток (Б). По оси ОХ (здесь и на рисунке 2) – ряд сгенерированных значений (n = 100)
А Б
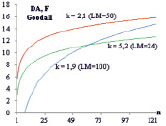
Рис. 2. Влияние числа меток на флуктуирующую (А) и направленную асимметрию (Б)
Аналогичная проверка была проведена для оценки изменчивости направленной асимметрии. Наименьший коэффициент регрессии (k = 1,9) был получен при LM = 100, наибольший – при LM = 24 (k = 5,2) (рис. 2).
Направленная асимметрия заметно превышала флуктуирующую асимметрию по величине F Гудолла при одинаковом p, меньше 0.0001. Уровень p двух видов асимметрии оставался по-прежнему высоким при различном числе меток. Проведенный анализ дал значимый результат уже при LM = 24, т. е. при 12 метках на правой и левой стороне листовой пластины. Однако нельзя ограничиваться малым числом меток, т. к. при сравнении большого числа выборок статистическая значимость может снижаться.
Таким образом, увеличение числа меток и объема выборки снижает ошибку прокрустова дисперсионного анализа и повышает значимость флуктуирующей и направленной асимметрии только в терминах межгрупповой изменчивости критерия Гудолла F, как аналога критерия Фишера.
Материал, собранный с одной делянки (с установленным составом удобрений) как экспериментальной единицы исследования, не может в строгом терминологическом понимании считаться истинной повторностью. Использование материала с повторных делянок может стать источником ошибки из-за пространственной неоднородности, т.к. увеличение степеней свободы нейтрализуется физико-химическими неучтенными факторами ландшафта.
Используемые метки, строго говоря, обладают свойствами полуметок, т.к. расставляются равномерно вдоль края листовой пластины, в отличие от меток первого типа, наносимых на определенные морфологические структуры. Это тоже может служить источником ошибки при определении формы листа, однако при определении асимметричности полуметки могут условно играть роль истинных меток первого типа. В некоторых работах [13; 14] полуметки рекомендуется менять на скользящие (sliding) метки, что, безусловно, следует принять во внимание в предстоящих исследованиях.
Количество меток несущественно влияло на значения направленной асимметрии, в то время как флуктуирующая асимметрия была более чувствительной к их числу, что объясняется меньшей долей ФА в общей асимметрии.
Большое значение имела систематическая ошибка измерения, зависящая от числа повторных измерений. Ошибка фотографирования занимала 11 % от общей ошибки в прокрустовом дисперсионном анализе, соответственно, 89 % приходилось на ошибку нанесения меток. При LM = 100 общая ошибка составляла около 4 % от суммы средних квадратов MS, включавшей: индивидуальную изменчивость (образец), различия в координатах меток (сторона) и взаимодействие обоих факторов (образец×сторона). При 24 метках ошибка занимала около 9 % от суммы MS [3]. В целом ошибка тестирования ФА составляла лишь доли процента (0,1-0,5 %) от величины ФА.
Предлагаем следующие рекомендации для проведения работ в области геометрической морфометрии:
а) наносить кривые в повторности по часовой и против часовой стрелки, с последующим разбиением на метки;
б) количество наносимых меток по краю листа должно быть не менее 50, за исключением неспаренных меток, наносимых по условной оси симметрии;
в) длина листовой пластины, зависящая от особенностей вегетации растения, должна быть стандартизирована в пределах 17-18 см или в другом узком диапазоне, например 19-20 см;
г) повторное фотографирование можно исключить в связи с незначительным влиянием на погрешность. Число повторностей нанесения меток на одно изображение мы рекомендуем увеличить до 4.
Заключение
При моделировании ошибки в прокрустовом дисперсионном анализе установлено, что сокращение числа наносимых меток менее 50 и количества образцов в выборке менее 100 приводит к систематической ошибке, снижающей величину F Goodall, т.е. различие между внутригрупповой и межгрупповой дисперсией, до 50 %.
Для определения такой популяционной характеристики, как стабильность развития, важно тестирование чистой ФА, лишенной примеси направленной асимметрии. Результат тестирования асимметрии зависит от обоих видов ошибки, как рандомной, так и систематической. Частотная характеристика выборки, например гетерогенность длины листовой пластины, может как снижать, так и увеличивать значение флуктуирующей асимметрии. Предпочтительнее использовать крупные листовые пластины, как более морфологически сформированные. Минимальный разброс в длине листьев теоретически снижает гетерогенность. Дальнейшее исследование будет направлено на рандомизацию выборок и определение рандомной ошибки, связанной с методическими особенностями сбора полевого материала.



