Прорывные паводки, образующиеся при разрушении искусственных и естественных грунтовых плотин вследствие их перелива, относятся к опасным гидрологическим явлениям и часто влекут за собой катастрофические последствия: значительный материальный ущерб и человеческие жертвы. Прорывы искусственных грунтовых плотин происходят в разных регионах нашей планеты с различными геоморфологическими условиями, а прорывы естественных перемычек приурочены, как правило, к труднодоступным горным районам [1]. В последнем случае речь идет о моренных и приледниковых озерах. Переполнение их котловин (благодаря интенсивному притоку талых ледниковых вод, выпадению большого количества осадков или поступлению большого объема воды в результате прорыва моренного озера, расположенного выше), а также уменьшение устойчивости плотины (в результате таяния ледяного ядра в моренной перемычке, фильтрации через рыхлый моренный материал, динамического движения ледяных глыб, снежных лавин и оползней, обвалов моренного материала и крупных валунов во время землетрясений) могут привести к запуску механизма прорыва и впоследствии спровоцировать сход селевых потоков [1-3].
В силу внезапности и быстротечности процессов прорывов организация наблюдений за ними крайне затруднена. Поэтому для изучения этих явлений целесообразным становится применение различных методов моделирования. В отечественной и зарубежной научной литературе достаточно много работ посвящено исследованию процесса прорыва искусственных грунтовых плотин [4-6] и внутриледниковых водоемов [7; 8]. Что касается прорывов естественных моренных плотин, то список опубликованных научных работ (особенно отечественных) не так обширен. В качестве примера можно отметить публикацию [3], где рассмотрены результаты моделирования прорывных паводков и селей в долине р. Гунт (Таджикистан) и семи долинах-притоках. Для этого была адаптирована двумерная модель движения водных и селевых потоков FLO-2D PRO (США) с использованием цифровой модели рельефа ALOS PALSAR (https://asf.alaska.edu/data-sets/sar-data-sets/alos-palsar/). Имеющиеся натурные данные о характеристиках прорывов в результате разрушений грунтовых плотин (время разрушения, морфометрия проранов, расходы воды) весьма ограниченны, несмотря на многочисленность таких событий, и часто базируются лишь на свидетельствах очевидцев. Многие случаи прорывов плотин не фиксировались сразу после самого события или не были точно и полно описаны. В этой связи оценка эффективности моделирования путем сравнения характеристик модельных гидрографов с наблюденными данными реальных прорывов вызывает определенные сложности.
В настоящей работе представлены результаты верификации модели расчета гидрографа прорыва при переливе через грунтовую дамбу. В отличие от моделей подобного класса [6; 9] авторами предложена аппроксимация поперечного сечения прорана, которая, по их мнению, более точно отражает процесс его развития; также предлагается учитывать изменение скорости потока в придонной части прорана на границе с грунтом. Расчетные гидрографы сопоставлялись с данными, которые были получены авторами в ходе физического моделирования. На основе проведенных численных экспериментов показано влияние изменения характеристик грунта на скорость эрозии.
Материалы и методы исследования
Модель расчета гидрографа при прорыве грунтовой плотины
Предложенная модель расчета гидрографа прорывного паводка разработана авторами и основывается на следующих представлениях:
– формирование прорывного паводка при переливе воды через гребень плотины начинается с момента, когда вода из подпруженного однородной искусственной плотиной или естественной моренной перемычкой водоема начинает течь по телу плотины и частично фильтроваться в нее;
– насыщение тела плотины водой ведет к снижению ее устойчивости, ввиду чего образовавшийся поток начинает ее разрушать и выносить частицы грунта, слагающего эту плотину;
– образование прорана происходит в центре гребня плотины, где уже имеется углубление малого размера; здесь происходит концентрация потока воды.
Если QB(t), QIN(t) и QS(t) – это переменные во времени расход воды через проран, расход воды притока, поступающего в водоем, и расход воды через водосбросы соответственно, то изменение объема водоема в случае его прорыва ΔV(t) за время Δt составит:
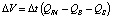 ,
,
или, переходя к бесконечно малым величинам,
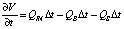 , (1)
, (1)
В качестве допущения примем, что течение воды через проран близко по параметрам к течению воды через водослив с широким порогом. Исходя из этого, для определения расхода воды через проран в каждый момент времени t, t > t0, где t0 – начальный момент времени, будем использовать уравнение [10]:
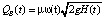 , (2)
, (2)
где ω(t) – площадь поперечного сечения потока; μ – коэффициент расхода, зависящий от типа водослива и условий его работы, изменяется в широком диапазоне (μ = 0,3÷0,6); g – ускорение свободного падения; H – напор воды, равный разности отметок поверхности воды в потоке zW(t) и дна прорана zB(t) (рис. 1):
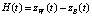 . (3)
. (3)
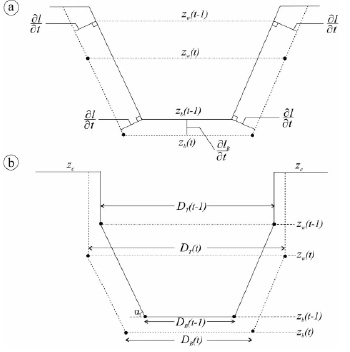
Рис. 1. Схема вычисления площади поперечного сечения потока (a) и площади прорана (b) Обозначения: DT(t) и DB(t) – ширина прорана в верхней и нижней частях прорана соответственно, 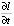 – скорость денудации, соответствующая средней скорости потока,
– скорость денудации, соответствующая средней скорости потока, 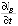 – скорость денудации, соответствующая донной скорости потока, zW(t) и zB(t) – отметка воды и отметка дна прорана
– скорость денудации, соответствующая донной скорости потока, zW(t) и zB(t) – отметка воды и отметка дна прорана
Подставляя выражение (3) в уравнение (2), получаем уравнение для определения расхода воды через проран на каждый момент времени:
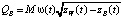 ,
,
где
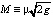 . (4)
. (4)
Отметка поверхности воды zW(t) может быть получена по зависимости объема водоема от его глубины 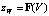 , которая предполагается известной, например, по результатам батиметрической съемки.
, которая предполагается известной, например, по результатам батиметрической съемки.
Соотношение для расчета ω(t) зависит от того, каким образом будет аппроксимирована форма поперечного сечения потока через проран, иными словами, как будет происходить развитие прорана. При моделировании чаще всего его форму аппроксимируют треугольником или трапецией [6].
Если DT и DB – ширина прорана в верхней и нижней части, а zC – отметка гребня плотины, то площадь поперечного сечения потока ω(t) и прорана Ω(t) на каждый момент времени, с учетом (4), можно представить как:
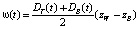 , (5)
, (5)
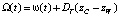 , (6)
, (6)
тогда,
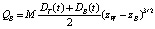 ,
,
или
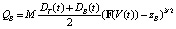 . (7)
. (7)
Предположим, что разрушение плотины и развитие прорана (изменение его размеров, а именно ширины и глубины) начинается в центральной части гребня плотины через некоторое малое и произвольно заданное нарушение поверхности. Приращение линейных размеров прорана, вызванные донной эрозией ΔlB(t), меньше, чем у его боковых частей Δl(t), поскольку скорость в придонном слое ниже среднего значения, используемого при расчете Δl(t). Для расчета площади живого сечения потока ω(t) на произвольный момент времени t, t ˃ t0, его форма аппроксимируется трапецией, как наиболее часто встречающейся при описании форм проранов при прорывах (рис. 1а). В то же время в процессе углубления прорана происходит подмыв боковых стенок и их обрушение, в результате чего поперечное сечение прорана принимает более сложную форму (рис. 1b). Практически это означает, что профиль прорана в пределах смоченного периметра остается трапецеидальным, а сверху – прямоугольным.
Таким образом, с учетом (5), (6) и (7), скорость приращения площади прорана можно записать следующим образом:
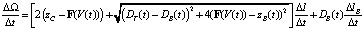 . (8)
. (8)
Значения скорости приращения линейных размеров прорана равна скорости эрозии E(t). Она определяется сдвиговым напряжением на эродируемой поверхности τ [11], инициируемым водным потоком, причем эрозия имеет место только в том случае, когда превышено некоторое пороговое значение сдвигового напряжения τс скорости эрозии.
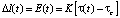 ,
,
где K – коэффициент эрозии, для расчета которого воспользуемся соотношением (9) по [6].
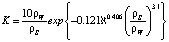 , (9)
, (9)
где ρS – плотность материала, из которого сложена плотина, ρW – плотность воды, 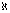 – доля содержания глины в грунте, из которого сложена плотина.
– доля содержания глины в грунте, из которого сложена плотина.
Соотношение для расчета τ(t) согласно [6]:
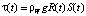 ,
,
или
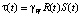 , (10)
, (10)
с учетом того, что γW = ρWg, где γ – удельный вес.
Если S(t) – энергетический уклон, согласно соотношению, предложенному в [6], определим как:
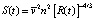 , (11)
, (11)
где 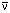 – средняя скорость потока воды, которая определяется как
– средняя скорость потока воды, которая определяется как 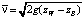 ; n – коэффициент Стиклера, зависящий от крупности частиц грунта, характеризуется значениями в интервале от 0.01 до 0.05 и определяется соотношением
; n – коэффициент Стиклера, зависящий от крупности частиц грунта, характеризуется значениями в интервале от 0.01 до 0.05 и определяется соотношением 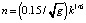 , где k – крупность частиц грунта. Энергетический уклон также рассчитывается для донной скорости νB, которая определяется по уравнению Караушева
, где k – крупность частиц грунта. Энергетический уклон также рассчитывается для донной скорости νB, которая определяется по уравнению Караушева 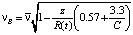 , где z – глубина погружения точки, C – коэффициент Шези, R(t) – гидравлический радиус потока,
, где z – глубина погружения точки, C – коэффициент Шези, R(t) – гидравлический радиус потока,
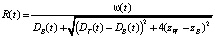 ,
,
или
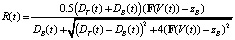 . (12)
. (12)
Воспользуемся для определения τc соотношением, предложенным в [14]:
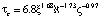 , (13)
, (13)
где ξ – индекс пластичности грунта, % (характеристика, отражающая способность грунта удерживать воду, для супесей изменяется в пределах 1-7 %, для суглинков 7-17 %, для глин больше 17 %), из которого сложена плотина, ς – пористость грунта.
Таким образом:
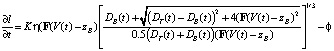 , (14)
, (14)
где 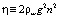 и
и 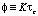
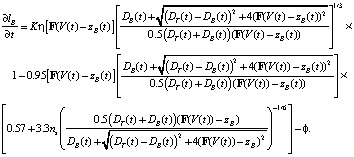 (15)
(15)
Скорости изменения элементов конфигурации прорана 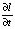 и
и 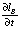 зависят от постоянных для каждого объекта величин K, η, ϕ и zC, и определяются соотношениями (14) и (15), его изменяющимися линейными размерами DT, DB, zB, а также уровнем воды zW. Скорость изменения величин DT и DB определяется через
зависят от постоянных для каждого объекта величин K, η, ϕ и zC, и определяются соотношениями (14) и (15), его изменяющимися линейными размерами DT, DB, zB, а также уровнем воды zW. Скорость изменения величин DT и DB определяется через 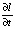 и
и 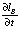 как
как
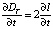 , (16)
, (16)
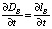 . (17)
. (17)
Скорость падения уровня воды и сам уровень воды zW определяются по объемной кривой, 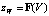 , с учетом вытекшей воды через проран и возможного пополнения озера (1б), т.е.
, с учетом вытекшей воды через проран и возможного пополнения озера (1б), т.е.
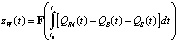 . (18)
. (18)
Подставляя полученные соотношения в (5) и численно решая полученное уравнение, найдем конфигурацию профиля прорана в каждый момент времени, а с учетом (1) получим изменяющийся во времени расход через него. Граничными условиями для решения краевой задачи выступают конфигурация прорана и расход на определенный момент времени или на момент завершения стадии (т.е. t → ∞), на который требуется знать общий объем вытекшей воды. Начальными условиями является объем воды в озере и его уровень, а также геометрические размеры дамбы. Так как модель не рассчитывает формирование первичного нарушения в теле плотины, обоснование и рекомендации к выбору его размеров были выполнены на основе численных экспериментов и приведены ниже.
Результаты исследования и их обсуждение
Численные эксперименты
Для проверки алгоритма модели на адекватность был выполнен ряд численных экспериментов: при неизменной геометрии плотины и водоема вводились разные размеры начального нарушения в дамбе, а также различные характеристики грунта при прочих равных параметрах модели. Характеристики плотины и водохранилища для численных экспериментов соответствовали Кокпектинскому водохранилищу, расположенному в Казахстане (длина плотины 940 м, высота плотины 12 м, объем водохранилища 2.7 млн м3), прорыв которого случился 31 марта 2014 г. [12].
На рис. 2a и 2b представлена серия расчетных гидрографов при разных размерах первичного нарушения в теле дамбы. Выбранный интервал значений ширины составлял от 1 до 10 м, что соответствовало от 0.1 % до 1 % длины дамбы, глубина первичного нарушения задавалась от 0.8 % до 8 % высоты плотины.
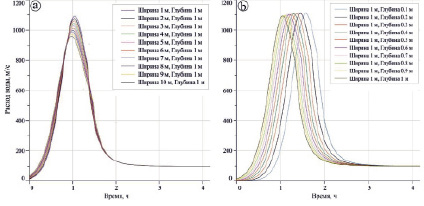
Рис. 2. Гидрографы при разной начальной ширине прорана (а) и глубине прорана (b)
Как показали расчеты, изменение ширины первичного нарушения при фиксированной глубине не влияет на время прохождения волны, форму гидрографа и время начала прорыва. Что касается максимального расхода, то чем больше ширина первичного нарушения при прочих равных условиях, тем меньше максимальный расход. Это достаточно логично, так как в этом случае происходит более быстрое увеличение расходов воды, что в свою очередь ведет к более стремительному истечению воды из водоема. Более интенсивное истечение приводит к уменьшению напоров и, соответственно, уменьшению скорости течения, вследствие чего значение максимального расхода становится меньше. При этом увеличение ширины в два раза от начальной (с 1 до 2 м) приводит к снижению максимального расхода на 2 %, а увеличение ширины в 10 раз от начальной (с 1 до 10 м) приводит к уменьшению максимального расхода всего лишь на 13.5 % (рис. 2a).
Увеличение глубины первичного нарушения тела дамбы при прочих равных условиях практически не оказывает влияния на значения максимального расхода (изменение глубины в 10 раз (с 0.1 до 1 м) изменяет расход примерно на 1.5 %), форму гидрографа и время прохождения волны паводка. В то же время значительно увеличивается время от начала перелива до достижения максимального расхода и спуска всего водоема: изменение глубины первоначального нарушения с 0.1 до 1 м увеличило время до 0.5 ч. Чем меньше первичная глубина, тем дольше будет происходить процесс размыва и позднее наступит максимальный расход воды, что также не противоречит природе протекания процесса.
Исходя из вышеизложенного, рекомендованные размеры первичного нарушения плотины предлагается задавать следующие: ширина не более 1 % от длины, а глубина не более 5 % от высоты дамбы. Именно в этих интервалах, как показали численные эксперименты, значения расходов меняются в пределах точности их измерений (5 %).
Проведенные численные эксперименты также показали, что в наибольшей степени модель «чувствительна» к таким входным параметрам, как удельный вес материала, слагающего плотину, и процент содержания в нем глины, поскольку от них зависит величина коэффициента эрозии. На рис. 3а приведены полученные авторами графики зависимости коэффициента эрозии от удельного веса материала и процентного содержания глины для грунтов, которые наиболее часто используются при строительстве плотин и встречаются в составе моренных дамб, согласно [13].
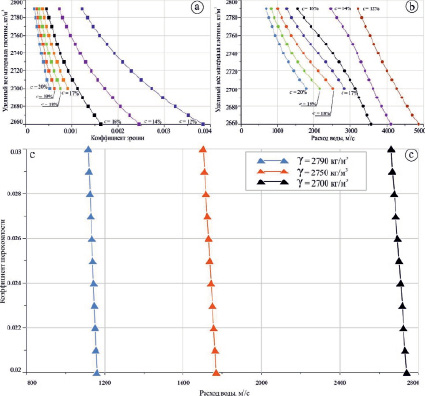
Рис. 3. Зависимость коэффициента эрозии от удельного веса материала плотины и процентного содержания глины в нем (a), зависимость расхода воды от удельного веса материала дамбы и процентного содержания глины в нем (b), зависимость расхода воды от величины коэффициента шероховатости (c)
Влияние вышеперечисленных параметров на величину максимального расхода воды проиллюстрировано на рис. 3б. Как видно из графиков, изменение содержание глины всего на 2 % для разных по гранулометрическому составу грунтов ведет к изменению величины максимального расхода до 20 %. Данная зависимость обусловлена влиянием этих факторов на скорость эрозии и, следовательно, на скорость разрушения плотины.
Что касается параметра ns – коэффициента шероховатости, то в интервале значений, характерных для земляных русел (0.02–0.03), которые наилучшим образом подходят для случаев прорывов, его изменение приводит к изменению величин расходов до 5 % (рис. 3c).
Физические эксперименты
Так как получить наблюденный гидрограф прорывного паводка возможно только в условиях эксперимента, верификация алгоритма модели была выполнена по данным, полученным в ходе серии физических экспериментов, проведенных на экспериментальной установке и в натурных условиях (рис. 4). Экспериментальный водоем представлял собой емкость, выполненную из монолитного поликарбоната размером 1×1×1.5 м, состоящую из двух отсеков.

Рис. 4. Фотографии процесса разрушения модельных дамб: эксперимент № 1 (a) и эксперимент № 2 (b)
Первый отсек размером 1×1×0.6 м заполнялся водой. Во втором отсеке сооружалась дамба. Между отсеками была установлена перегородка с прямоугольным отверстием (0.05×0.15 м) для перетекания воды. Во время заполнения первой емкости до начала эксперимента отверстие закрывалось затвором. Для фиксации уровня воды на стенке второй емкости была установлена мерная шкала. Натурные эксперименты были проведены в июле 2018 г. на Кавказе (рис. 4b) [14].
Расходы воды через проран по результатам экспериментов определялись по формуле:
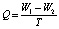 , (19)
, (19)
где Q – расход воды через проран, л/с; W1 и W2 – объемы при разных уровнях воды (дискретность 1 см), Т – время, за которое уровень воды упал на 1 см. Для оценки сходимости рассчитанных по модели и полученных в результате эксперимента гидрографов был использован коэффициент Нэша-Сатклиффа (NS) [15], рекомендованного Американской ассоциацией гражданских инженеров для оценки состоятельности моделей стока, а также используемого Всемирной метеорологической организацией для сравнительного анализа моделей. Диапазон значений критерия находится в пределах от -∞ до 1, в общем случае моделирование признается удовлетворительным при NS > 0.5. В качестве примера приведем результаты экспериментов с наилучшим, удовлетворительным и наихудшим значениями NS (размеры дамб и характеристики грунтов представлены в таблице).
Характеристики экспериментальных плотин и водоемов
|
№ п/п |
1 эксперимент |
2 эксперимент (натурный) |
3 эксперимент |
|
Грунт |
Супесь |
Моренный грунт |
Супесь |
|
Уд. вес грунта/ % глины |
2730 / 16 % |
2630 / 5 % |
2590 / 6.9 % |
|
Высота, м |
0.2 |
0.17 |
0.35 |
|
Толщина по подошве, м |
0.46 |
0.4 |
0.71 |
|
Длина по гребню, м |
1 |
1.2 |
1 |
|
Ширина гребня, м |
0.1 |
0.05 |
0.05 |
|
Длина откосов, м |
0.29 и 0.33 |
0.3 и 0.3 |
0.55 и 0.55 |
|
Глубина начального прорана, м |
0.005 |
0.005 |
0.01 |
|
Объем водоема, м3 |
0.183 |
0.203 |
0.312 |
Отметим, что, так как целью моделирования была проверка расчетного алгоритма, физические модели (плотины) имели произвольно заданные размеры и не являлись уменьшенными копиями известных плотин.
Полученные в результате эксперимента наблюденные и смоделированные гидрографы прорывов искусственных водоемов (рис. 5) характеризуются асимметричной формой (за исключением эксперимента № 2 (рис. 5b)): быстрым увеличением расходов воды и более плавным снижением их значений после достижения максимума. При моделировании не учитывается спонтанное обрушение грунта с бортов прорана, которое ведет к появлению локальных увеличений расходов воды на наблюденных гидрографах (рис. 5 a, b).
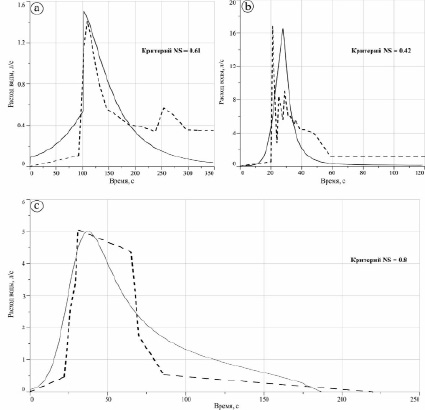
Рис. 5. Наблюденные (пунктирная линия) и смоделированные (сплошная линия) гидрографы прорывного паводка для эксперимента № 1 (a), эксперимента № 2 (b) и эксперимента № 3 (с)
Анализ смоделированных и полученных в результате физических экспериментов гидрографов показал: наступление пиков прорывных паводков практически совпадает по времени; расхождение в наступлении максимальных расходов воды составляет от 5 (эксперимент № 1, рис. 5a) до 7 секунд (эксперименты № 2 и № 3, рис. 5b и 5c), что является отклонением не более чем на 5.5 % от наблюденных. Наибольшее отклонение значений смоделированных максимальных расходов от полученных в результате экспериментов составило 6 % (эксперимент № 1, 5a). При проведении эксперимента № 2 (рис. 5b) произошло спонтанное обрушение грунта на 19-й секунде, что привело к несовпадению пиков гидрографов. Именно для этого случая критерий NS принимает наименьшее значение – 0.42. В случае эксперимента № 1 NS составил 0.61, что говорит об удовлетворительной сходимости, а для эксперимента № 3 – 0.8, что свидетельствует о хорошей сходимости гидрографов и, следовательно, о высоком качестве моделирования. В последнем случае образование прорана протекало исключительно за счет размыва тела дамбы, без спонтанных обрушений стенок, формирования фильтрационного канала (piping) и других нарушений.
Заключение
Представленная в работе модель расчета гидрографа прорывного паводка относится согласно Paul J. Visser [9] к физически обоснованным моделям прорыва плотин, которые используют принципы гидравлики, эрозии и механики почвы для разработки пошаговых во времени решений описания процессов увеличения прорана и гидрографа прорыва. Опыт ее верификации показал, что результаты моделирования, согласно коэффициенту NS, в целом получены удовлетворительные, демонстрирующие работоспособность алгоритма. Как и во всех моделях данной группы, остается не решенным вопрос о формировании начального нарушения в теле плотины. Тем не менее по результатам численных экспериментов авторами предложен количественный критерий выбора размеров начального нарушения в теле плотины. Численные эксперименты подтвердили чувствительность модели к изменению коэффициента эрозии, который зависит от гранулометрического состава грунтов, слагающих плотины. В частности, изменение содержания глины всего на 2 % для разных по гранулометрическому составу грунтов ведет к изменению величины максимального расхода до 20 %. В этой связи дальнейшие шаги по совершенствованию алгоритма должны заключаться в учете неоднородностей в структуре искусственных грунтовых плотин и естественных моренных перемычек.
Модель имеет простой в реализации алгоритм и, несмотря на определенные ограничения, может быть использована для оценочных расчетов характеристик прорывных паводков, формирующихся при переливе через грунтовые дамбы.
Работа выполнена при поддержке гранта РФФИ № 20-05-00343 А «Выявление особенностей протекания процесса прорывов озер оазисов Антарктиды на основе данных полевых исследований и математического моделирования».



