При интерпретации геолого-геофизических данных, изучении структурно-тектонического строения территории и выявлении факторов, влияющих на формирование залежей углеводородов, используются физико-геологические модели. Построение модели включает в себя моделирование геологического разреза на основе имеющейся геолого-геофизической информации и современных программных средств. В результате геологическая модель должна удовлетворять априорной информации с заданной степенью точности.
Целью работы является систематизация знаний о типах моделей, принципах моделирования, технологий, используемых для изучения геологической среды с целью выявления зон, перспективных на наличие залежей углеводородов. А также выявление особенностей формирования физико-геологической модели с использованием продуктов, разработанных в УГТУ, на примере площадей Косью-Роговской впадины Предуральского краевого прогиба.
Материал и методы исследования
Геологические объекты изучаются на основе модельных представлений. При моделировании происходит упрощение формы, размерности принятых физических характеристик среды, например плотности, поэтому построенные модели всегда проще реальной геологической среды.
В геофизике широко распространены понятия модель среды (геологическая, физико-геологическая, дающая представления о распределении плотности, скоростная, позволяющая судить о скоростных характеристиках среды) и модель поля (гравитационного, временного, магнитного). Модель геологической среды описывается параметрами и связями [1]. Параметры описывают свойства объекта, связи определяют соотношения между параметрами. В науках о Земле понятие физико-геологической модели (ФГМ) было введено Г.С. Вахромеевым и А.Ю. Давыденко [2]. Академик РАН, доктор физико-математических наук В.Н. Страхов [3] описывал ФГМ следующим образом. Нижний, базовый уровень составляет геологическая модель (ГМ), при ее построении выделяются геологические слои и структуры. Следующий уровень – петрофизическая модель (ПФМ), представляющая собой наполнение геологической модели физическими параметрами. Третий уровень ФГМ – математическая модель (ММ). Именно она используется для решения прямой и обратной задач геофизики [4]. Математическая модель объекта – приближенное формализованное его описание с помощью математических понятий и объектов, включающих в себя геометрические образы, уравнения, алгоритмические правила и др., связывающие поля со средой [5].
Комплексная интерпретация геофизических данных в своей активной постановке предполагает совместное решение обратных задач нескольких методов, например сейсморазведки и гравиразведки. Пассивная комплексная интерпретация основана на решении обратной задачи для одного метода, а данные других методов используются в проинтерпретированной и не подлежащей варьированию форме.
Результаты исследования и их обсуждение
В УГТУ под руководством профессора, доктора физико-математических наук А.И. Кобрунова была создана и действовала несколько десятилетий научно-педагогическая школа «Математическое моделирование, теория, методы и компьютерные технологии решения обратных задач геофизики». Внедряемые достижения коллектива разнообразны по содержанию: это новые теоретические выводы и методы, методики и технологии, программные продукты; научные исследования; практическое внедрение результатов научно-исследовательской работы. Предложенные разработки успешно реализованы на различных площадях Тимано-Печорской нефтегазоносной провинции [6].
Рассмотрим наиболее распространенные физико-геологические модели, используемые при решении задач комплекса гравиразведки и сейсморазведки. Плотностная модель используется для решения задач локального прогнозирования. Структурная геолого-геофизическая модель применяется в случае слоистого строения среды [7; 8].
Вертикальная производная гравитационного потенциала uz(v0), где v0 = (x0, y0, z0) и точка (x0, y0) = s0 ∈ E0 регистрируется на поверхности в E+(z > 0) с уравнением z0 = ψ(s0) задана соотношением между uz(v0) и σ = σ(v), v = (x, y, z):
Aσ(v) = u(s0) (4)
Критерий оптимальности в квадратичной метрике. Вся информация об искомом распределении плотности включается в критерий оптимальности [4].
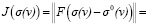
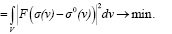 (5)
(5)
Решение задачи (4), (5):
σ(v) = σ0(v) + F-1F*-1A*ζ(s0) (6)
Здесь ζ(s0) – функция, определяющая класс оптимальных решений (4,5), F – линейный замкнутый оператор, имеющий обратный, A* – оператор, сопряженный к А, F-1 – обратный к F. Подставив (6) в (4), строим искомое оптимальное распределение.
Критерий оптимальности в равномерной метрике. Итерационный процесс нахождения решения (6) [4]:
σn+1(v) = σn(v) + αnKφn(s0),
n = 0, 1, 2, …, σ0(v) = σ0(v), (7)
αn – параметр релаксации.
Критерий оптимальности примет вид:
sup│K-1[σ(v) – σ0(v)]│→ min, v ∈ V (8)
Оператор K содержит информацию о достоверности построения различных компонент нулевого приближения, а также о корреляционной связи между различными параметрами.
Интегральный критерий оптимальности. Пусть в (1) задано нулевое приближение σ*(v)и оценена погрешность построения нулевого приближения σ*(v) в каждой точке v ∈ V. Подбираем такое σ(v), которое удовлетворяет уравнению (5) и имеет меньшую меру расхождения с σ*(v):
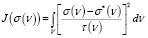 (9)
(9)
Выражение (9) и представляет собой интегральный критерий для плотностной задачи [4]. Для территории, достаточно разбуренной скважинами, параметр τ близок к 0, а по мере удаления от таких мест – к 1.
Критерий оптимальности на основе нечетких множеств. При формировании геолого-геофизической модели объекта данные можно представлять как нечеткие величины, операции над ними проводить согласно теории нечетких множеств [9]. Тогда в (1) A – оператор, отображающий распределение параметра плотности с определенной мерой доверия к значениям σ(v) ∈ D(A) = L2(V) из области V, в распределение наблюдаемого гравитационного поля u(s0) на дневной поверхности E0, s0 ∈ E0. Нечеткая величина σ полностью характеризуются функцией принадлежности 0 ≤ μ(σ) ≤ 1 [10].
Эволюционно-динамическое моделирование (ЭДМ). Эволюционно-динамическое моделирование состоит в представлении и изучении той части эволюционных процессов в литосфере, которая связана с динамикой элементов, входящих в состав изучаемой системы. Включение ЭДМ в решение обратных задач гравиметрии позволяет повысить информативность интерпретационных процедур, обеспечить единственность задач инверсии за счет активного вовлечения в вычислительный процесс данных о динамическом генезисе изучаемых объектов и динамических процессов, приведших к их формированию [11].
Алгоритм совместного решения задач. Искомая модель среды x1(v) должна соответствовать наблюдаемому полю u1(s): A(x1) = u1(s). Модель x2 этой же среды соответствует некоторому другому полю u2(s): B(x2) = u2(s). Задача сводится к нахождению пары распределений, каждое из которых удовлетворяет своему полю, а сами эти распределения – ближайшие друг к другу среди всех пар [4]:
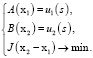 (10)
(10)
Нулевое приближение структурной плотностной модели строится по сейсмическим данным. Совместное решение обратных задач сейсмо-, гравиразведки позволяет построить согласованную модель, имеющую две компоненты – структурную плотностную и скоростную модели, распределение плотности в структурной плотностной модели, компенсирующее остаточную невязку.
Рассмотрим программные продукты, позволяющие решать обратные задачи гравиразведки. На начальном этапе развития методов решения обратных задач гравиразведки участниками научной школы были созданы программные средства Sigma, Gran, позволяющие решать плотностные и структурные обратные задачи методом подбора. Затем была разработана автоматизированная система профильной комплексной интерпретации грави-сейсмических данных GCIS (совместно с Петровским А.А.) [12], позволяющая решать обратные задачи гравиразведки и сейсморазведки на основе комплексной интерпретации геофизических данных. Далее была разработана технология интегрированной инверсии геофизических полей для формирования моделей глубинного строения, реализованная в программных модулях PlayGround, EvDynInversion [13] и программном комплексе GeoVIP [13].
Примеры моделирования. Представим результаты моделирования геологической среды на примере комплексной интерпретации данных гравиразведки и сейсморазведки на примере площадей Косью-Роговской впадины Предуральского краевого прогиба.
Геолого-плотностная модель, представленная на рисунке 1, была составлена по линии VI-VI1 (сейсмические профили 8211-01, 8111-05, 7911-13, 50488-04) в результате комплексной интерпретации гравиразведки и сейсморазведки в пассивной форме.
В распределении плотностей на модели отображаются Интинская, Кожимская взбросо-надвиговые структуры и Кочмесская карбонатная платформа с рифами в нижнепермских породах с толщинами 400-500 м, которые замещаются на север, восток, юг депрессионными доманикоидными отложениями. Они перекрыты мергелисто-глинистыми породами, компенсирующими рельеф карбонатной платформы, и отображаются на плотностном разрезе аномалиями пониженной плотности до 2.66 г/см3. Характер дислокаций Интинско-Лемвинской складчатой зоны находит свое отражение в виде плотностных зон со значениями до 2.68 г/см3.
Расхождение в значениях рассчитанного и наблюденного гравитационного поля в результате решения обратной плотностной задачи гравиразведки составило 0,86 мГал, что является допустимым.
Геоплотностная модель (рис. 2) по региональному профилю 13РС, расположенному в центральной части Косью-Роговской впадины, соединяет Берганты-Мыльскую структуру и структуры Прилемвинской складчато-покровной зоны. На графике поля силы тяжести отмечается уменьшение значений Δg в восточном направлении.
Положительные структурные единицы – Берганты-Мыльская структура и Прилемвинский вал – хорошо отображаются в гравитационном поле. Терригенный комплекс, включающий породы пермской системы, дифференцирован плотностными границами, имеет складчатый характер, и его складки согласуются со складками нижележащего карбонатного комплекса. В карбонатном комплексе следует обратить внимание на изменение плотностей на Берганты-Мыльской структуре (2,72-2,76 г/см3), что соответствует изменению разреза доманиково-фаменской Нерцетинской атолловидной постройки, замещаемой менее плотными глинисто-мергелистыми породами.
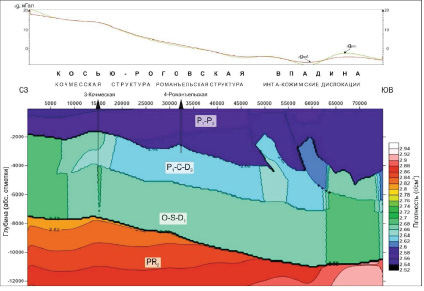
Рис. 1. Геоплотностная модель по региональному профилю 12РС
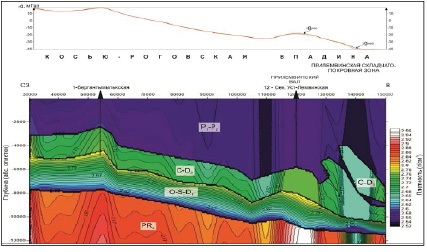
Рис. 2. Геоплотностная модель по региональному профилю 13РС
Прилемвинский вал содержит рифовые постройки верхнего девона-карбона, в которых плотности изменяются за счет чередования плотных и пористо-кавернозных пород (от 2,72 до 2,78 г/см3). Ордовикско-нижнедевонский, терригенно-карбонатный комплекс на плотностной модели характеризуется высоким градиентом плотности от 2,54-2,62 г/см3 в нижней части разреза (отложения ордовика) до 2,72-2,78 г/см3 – в верхней. Комплекс протерозойских отложений собран в складки, которые иногда имеют вид тектонических блоков, плотность пород в которых превышает 2,90 г/см3. Невязка между рассчитанным и наблюденным гравитационным полем в результате решения обратной задачи гравиразведки составила 1,05 мГал.
Выполненные в результате профильного моделирования плотностные модели интерполировались по данным сети профилей. Для уточнения поведения литологических толщ и выделения аномальных плотностных участков было выполнено вычисление пространственного гравитационного эффекта от всей толщи осадочного чехла и фундамента. Полученные геоплотностные срезы показывают в площадном виде распределение плотности в различных структурно-тектонических единицах.
При построении и интерпретации полученных срезов и геоплотностных моделей были использованы структурные карты: по кровле карбонатов, подошве визейского яруса нижнего карбона, подошве доманикового горизонта верхнего девона, кровле фундамента, также геолого-геофизические разрезы по региональным и сейсмическим профилям.
Пример плотностного среза с отметкой -1500 метров показан на рисунке 3. Центральная и восточная часть занята областью развития пермских терригенных осадков, характеризующихся пониженными значениями плотности 2,5-2,58 г/см3, что показывает преимущественное развитие терригенных пород, сменяемых на западе карбонатными отложениями гряды Чернышева.
В северо-восточной части наблюдается участок с повышенными плотностными характеристиками до 2,7-2,74 г/см3, относимый к Воркутскому поперечному поднятию, Ярвожской структуре, и характеризует породы нижнепермско-каменноугольного возраста. Северо-западная часть исследуемой территории охватывает гряду Чернышева, разрез осадочного чехла которой на этой отметке составляют отложения карбонатного комплекса плотностью 2,68-2,76 г/см3. На представленном срезе отобразились элементы рельефа пластов в нижнепермских терригенных отложениях.
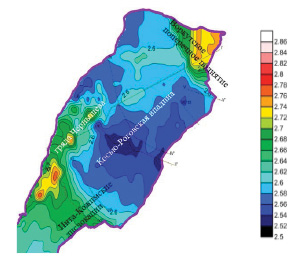
Рис. 3. Срез на глубине 1500 м
Отчетливо прослеживается перемычка (седловина) между грядой Чернышева и Кожимским поднятием Приполярного Урала, в которой ниже по разрезу сосредоточены открытые месторождения углеводородов Кочмесской ступени и Инта-Кожимских дислокаций. Седловиной менее плотных пород соединены гряда Чернышева, Берганты-Мыльская структура, Верхнероговское поднятие и Воркутское поперечное поднятие. Внутренний борт Косью-Роговской впадины занимает Восточно-Лемвинская складчато-покровная зона, сложенная породами Лемвинского аллохтона. Аномальной плотностной зоной со значениями 2,6-2,62 г/см3 отмечается участок нижнепермских отложений между южным окончанием гряды Чернышева и Интинской складчато-чешуйчатой зоной, что связано с развитием взбросов и взбросо-надвигов.
Заключение
В работе проведен анализ видов моделей геологической среды, используемых для ее изучения. Описаны принципы моделирования, особенности построения ФГМ. Представлены используемые в УГТУ программные продукты, позволяющие строить ФГМ на основе совместного решения задач гравиразведки и сейсморазведки. Приведены результаты моделирования с использованием указанных продуктов. При решении обратных задач (гравиразведки) в данной работе использовался интегральный критерий оптимальности и критерий, основанный на нечетком представлении данных. Полученные таким образом модели позволяют уточнять строение территории и определять области и зоны плотностных неоднородностей, влияющие на формирование залежей углеводородов.



