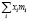В современной промышленности часто встречаются устройства, работающие с загрузочными зернистыми слоями, как стационарные, так и подвижные [1, 2]. К таким устройствам, в частности, относятся обжиговые конвейерные и агломерационные машины для обогащения рудного сырья в металлургической, химической и горно-обогатительной промышленности. Расчёт таких устройств требует знания аэродинамических характеристик подвижного плотного слоя кускового и окомкованного рудного сырья с перекрёстной подачей газа-теплоносителя [3, 4]. По гранулометрическому составу, как правило, чаще встречаются полифракционные системы, включающие широкие классы по размерам [5, 6]. Геометрическая структура таких систем будет сильно зависеть от степени неоднородности или полидисперсности. Аэродинамические параметры динамического плотного слоя определяются главным образом геометрическими характеристиками полифракционной засыпки рудного сырья и режимом функционирования обжиговых конвейерных машин [7, 8].
Цель настоящего исследования – провести натурные эксперименты по аэродинамическому сопротивлению двухкомпонентных смесей шаров и полифракционной засыпки кускового фосфоросодержащего рудного сырья; исследовать изменения аэродинамического сопротивления в изотермических и неизотермических условиях; разработать методику расчёта аэродинамического сопротивления полифракционного слоя.
Объект исследования – движущийся на конвейере обжиговой или агломерационной машины плотный слой кускового или окомкованного фосфоросодержащего рудного сырья, с перекрёстной подачей газа-теплоносителя.
Материалы и методы исследования
Основными геометрическими характеристиками неподвижного плотного слоя кускового и окомкованного фосфоросодержащего рудного сырья являются его порозность и удельная поверхность. Эти усреднённые параметры зависят от способа укладки слоя, гранулометрического состава, габаритов слоя. В качестве характерного геометрического размера принимают средний размер элементов слоя, для полифракционного слоя различают средневесовой диаметр
,
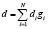или среднеповерхностный
,
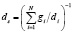где di – средний диаметр i-й фракции, gi – весовая доля i-й фракции. Порозность определялась экспериментально
ε = 1 – ρн / ρм,
где ρн – насыпная плотность, кг/м3, ρм – плотность материала, кг/м3. Удельная поверхность засыпки определялась соотношением:
,
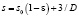где s0 – удельная поверхность элементов слоя, м2, D – диаметр рабочего участка, м. Для монофракционных засыпок шаров удельная поверхность определяется как s0 = 6 / d. Для полифракционных засыпок из шаров удельная поверхность слоя определяется соотношением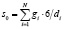 
. Для полифракционных засыпок из частиц неправильной формы определение удельной поверхности основывается на методике использования коэффициента формы зерна:
, 
, 
,
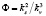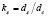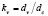где dc – среднеситовой, ds – эквивалентный по поверхности, dv – эквивалентный по объёму диаметр зерна. Эквивалентные диаметры определяются соответственно:
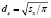и 
,
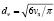где sз, vз – соответственно поверхность и объём зерна. Тогда удельная поверхность зерна полифракционного слоя будет определяться как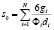 
.
Особенностью полифракционных засыпок является способность мелких фракций заполнять промежутки между крупными элементами, тем самым резко снижая среднюю порозность слоя. Это явление характеризуется способом укладки и степенью неоднородности засыпки. В различных источниках под степенью неоднородности понимается или отношение диаметра крупной фракции к диаметру мелкой фракции или наоборот. Нами принят коэффициент неоднородности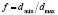 
.
Движение газа в слое подчиняется уравнению Навье – Стокса. Учитывая, что во многих промышленных установках с зернистым слоем скорость фильтрации газовой среды невелика, то можно считать газ несжимаемым. Однако сложность геометрической структуры затрудняет выполнить аналитически граничное условие: отсутствие скольжения на поверхности [9, 10]. В большинстве случаев можно пренебречь гравитационной составляющей уравнения Навье – Стокса.
С принятыми допущениями для усреднённых значений давления и скоростей газа-теплоносителя выражение для перепада давления вдоль потока будет иметь вид
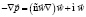. (1)
Для анализа уравнения (1) был предложен ряд моделей.
В области преобладания сил вязкости уравнение движения на основе капиллярной модели преобразуется к уравнению Козени – Кармана:
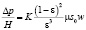, (2)
где K – константа Козени – Кармана, определяемая экспериментально для шаров 4÷4.5, s0 – удельная поверхность элементов слоя, Н – высота слоя.
Для слоя шаров:
.
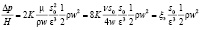Тогда коэффициент гидравлического сопротивления слоя:
,
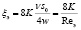где v – кинематическая вязкость потока, Reэ – эквивалентное число Рейнольдса.
Простейшая капиллярная модель и более сложная сетевая не учитывают многих особенностей реального слоя, таких как наличие застойных зон [11, 12].
Для модели из ансамбля шаров Хаппелем получено уравнение
,
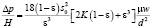которое отличается от (2) поправкой ε3. Введение такой поправки позволяет получить плавный переход к закону Стокса для омывания одиночного шара, что получается при ε → 1.
В областях течения, где влияют и силы вязкости, и инерционные из анализа метода размерностей уравнения перепада давлений в слое в общем виде будет
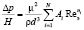. (3)
Обычно ограничиваются двумя первыми членами суммы (3), причём показатель степени для первого слагаемого, характеризующего вязкостный режим, получается равным нулю n1 = 0, а n2 = 2, характеризующий второй предельный случай – инерциальный режим. На практике чаще встречаются интерполяционные уравнения вида
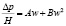, (4)
а для коэффициента аэродинамического сопротивления:
,
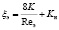тогда уравнение (4) преобразуется к виду
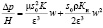, (5)
где Ки – инерционная составляющая сопротивления.
Эксперименты проводились на лабораторной установке, адаптированной авторами для проведения настоящих исследований, состоящей из рабочего участка высотой 0,5 м с внутренним диаметром для шаров 0,225 м, для кусковых засыпок – 0,3 м. Для выравнивания скорости газа на выходе в участок установлен ресивер с соплом на выходе с коэффициентом неравномерности 0,95. Для подогрева воздуха служит нагреватель, для получения более высоких температур использовалась камера сгорания, работающая на сжиженном газе – смеси пропана и бутана. Расходы воздуха и газа измерялись диафрагмами «четверть круга», температуры и температурные напоры регистрировались потенциометрами. Перепады давления в слое измерялись наклонными микроманометрами. Для усреднения давления по сечению установлены по три импульсные трубки, всего замеры проводились по четырём сечениям. Воздух нагнетался вентилятором высокого давления.
Перед исследованием полифракционных засыпок были проведены опыты с монофракционными слоями шаров с диаметром 16,67; 14,15; 9,51; 7,97 и 6,75 мм. Коэффициенты аэродинамического сопротивления определяли как
,
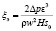где w – скорость потока газа-теплоносителя на свободное сечение, м/с.
После обработки результатов по коэффициенту аэродинамического сопротивления слоя шаров по методу наименьших квадратов усреднённая зависимость получилась:
,
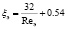что удовлетворительно совпадает с известными зависимостями, при этом константа Козени – Кармана получилась равной K = 4, а инерционная составляющая Ки = 0,54 при средней величине порозности ε = 0,36.
При исследовании полифракционных засыпок использовались смеси шаров вышеуказанных диаметров.
Изменение структуры слоя хорошо заметно по зависимости порозности слоя от содержания мелкой фракции и степени неоднородности. Для смеси шаров диаметром 16,67 и 6,35 при содержании мелких шариков 30 % по весу наблюдается минимальное значение порозности 0,295. Такое резкое снижение порозности объясняется соотношением диаметров. При кубической укладке шаров большего диаметра промежуток между шарами составляет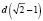 
, при диаметре 16,67 мм это будет 6,7 мм, то есть мелкие шарики свободно могут размещаться между крупными, а при степени неоднородности близкой к 0,5 зависимость порозности от весовой доли мелкой фракции получается более плавной, без резкого минимума.
С увеличением содержания мелкой фракции удельная поверхность слоя увеличивается, так как для мелкой фракции удельная поверхность больше. Обработка результатов по коэффициентам аэродинамического сопротивления слоя смесей шаров по методу наименьших квадратов даёт следующие значения расчётных формул.
При степени неоднородности f менее 0.5:
.
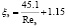При степени неоднородности f сравнимой с 0.5:
.
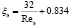Чем больше соотношение между диаметрами крупной и самой мелкой фракций, тем сильнее влияние на геометрическую структуру.
Результаты исследования и их обсуждение
Разработана методика расчёта сопротивления слоя при неизотермических условиях на основе позонного разделения слоя. Аэродинамическое сопротивление отдельных зон рассчитывается по уравнению
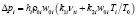, (6)
где hi – высота зоны, м; ρ0i – плотность газа в зоне, т/м3; w0i – скорость газа в зоне, м/с; vti – кинематическая вязкость газа при средней температуре в зоне, м2/с; Ti – средняя температура в зоне, К; k1i, k2i – коэффициенты аэродинамического сопротивления отдельных зон,
, 
,
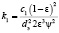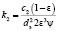где c1, c2 – константы в интерполяционной формуле для коэффициента аэродинамического сопротивления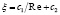 
, dэ – эквивалентный диаметр зерна; ψ – коэффициент формы зерна.
Полагая постоянными рассчитанные коэффициенты в каждой зоне, зная температурное распределение по высоте слоя, рассчитывается по уравнению (6) сопротивление отдельных зон и суммированием получают общее сопротивление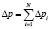 
.
Сопротивление слоя при высоких температурах во многом определяется свойствами потока, особенно вязкостью. Общеизвестно, что вязкость зависит от состава газового потока и сильно от температуры [13, 14]. Часто зависимость кинематической вязкости от температуры представляют в виде многочлена второй степени по температуре: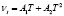 
.
Предлагается методика расчёта сопротивления неизотермического слоя как условно изотермического по температуре эквивалентной, которая определяется как
Tэкв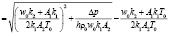 
. (7)
Температура, рассчитанная по этой формуле, на 5–15 % выше среднеинтегральной, следовательно, не рекомендуется рассчитывать сопротивление по среднеинтегральной температуре.
Для исследования сопротивления полифракционного слоя при неизотермических условиях нами использовалась засыпка фосфоросодержащего рудного сырья гранулометрического состава, представленного в табл. 1.
Таблица 1
Гранулометрический состав фосфоросодержащего рудного сырья
|
di, мм |
60 |
45 |
35 |
25 |
12,5 |
2,5 |
|
ξi |
0,0595 |
0,201 |
0,293 |
0,289 |
0,152 |
0,005 |
Прогрев слоя осуществляется продуктами сгорания пропан-бутановой смеси следующего состава:
, 
,
, 
.
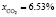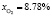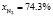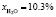Динамическая вязкость смеси рассчитывалась по формуле Хеннинга и Цепперера:
,
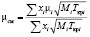где хi – молярная доля, μi – вязкость, Мi – молекулярная масса, Ткрi – критическая температура i-го компонента.
Изменение динамической вязкости от температуры рассчитывалось по формуле Улыбина:
,
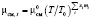где
.
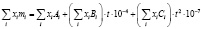Коэффициенты многочлена Аi, Вi, Сi для различных газов представлены в табл. 2.
Таблица 2
Постоянные аппроксимационного многочлена в формуле динамической вязкости
|
Газ |
A |
B |
C |
|
|
CO2 |
0,942 |
2,1 |
0,56 |
115,5 |
|
O2 |
0,76 |
1,4 |
0,64 |
70,2 |
|
N2 |
0,753 |
1,3 |
0,4 |
59,5 |
|
H2O |
1,082 |
0,25 |
0 |
108 |
Расчёт аэродинамического сопротивления полифракционного слоя при неизотермических условиях производился по уравнению (5), при этом принимались постоянными константа Козени – Кармана, полученная при температуре T0 = 273 K, и инерционная составляющая, равные соответственно К = 7 и К = 1,2.
Сопротивление рассчитывалось численным интегрированием по высоте слоя:
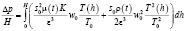. (8)
Использование условно изотермического слоя по эквивалентной температуре, рассчитанной по (7) даже для слабонеизотермических распределений, даёт значительное отклонение от уравнения (8). Эквивалентные температуры значительно превышают среднеинтегральные и в некоторых случаях превышают максимальную температуру в слое, что лишено физического смысла [15].
Следует рассчитывать сопротивление в неизотермическом полифракционном слое по уравнению (8).
Заключение
По проведенным в работе исследованиям аэродинамики полифракционных засыпок в изотермических и неизотермических условиях на примере смесей шаров и кускового фосфоросодержащего рудного сырья можно сделать следующие выводы.
1. Структура слоя из смеси шаров зависит от степени неоднородности. Минимальная порозность слоя соответствует весовой доле мелкой фракции 30 %.
2. Получены значения константы Козени – Кармана и инерционной составляющей для двух значений коэффициента неоднородности.
3. При неизотермических условиях расчёт сопротивления слоя необходимо проводить с учётом изменения свойств потока газа-теплоносителя. Расчёт по среднеинтегральным температурам условно изотермического слоя приводит к значительным погрешностям.
Исследование выполнено за счет гранта Российского научного фонда № 22-11-00335, https://rscf.ru/project/22-11-00335/.