Изучение множества природных процессов, особенно происходящих под ледниковым покровом и в его толще, практически невозможно выполнить in situ. Прямые измерения либо чрезвычайно сложны и дорогостоящи, либо вовсе технически неосуществимы на современном этапе развития. В связи с этим единственным способом изучения процессов, протекающих в этих средах, а также прогнозирования их состояния в будущем является математическое моделирование. Именно по этой причине ещё на заре планомерного изучения труднодоступных полярных регионов начали создаваться первые математические модели, в том числе динамики ледниковых покровов и процессов, происходящих на их ложе. Несмотря на простоту и большое количество допущений в этих моделях, все они имели в своей основе фундаментальные законы, выраженные через уравнения матфизики. Впоследствии, по мере широкого внедрения компьютерной техники, математические модели постепенно усложнялись [1-3] и обретали формы компьютерных программ. Однако применительно к оценке субгляциальных процессов они всё также основывались на решении фундаментальных уравнений переноса и теплопроводности. Единственность решения достигалась путём задания начальных и граничных условий (краевая задача). По понятным причинам даже наиболее простые модели не могут быть решены аналитически и реализуются лишь численными методами.
В настоящее время имеется множество методов численного решения уравнений матфизики, которые сводятся к интегрированию посредством применения различных конечно-разностных схем. Однако они, как и все приближённые методы вычислений, имеют свои недостатки. Имеется ряд работ, в которых с позиций математики обсуждаются те или иные аспекты различных конечно-разностных схем. В этом направлении много работал академик Александр Андреевич Самарский, создатель Всесоюзного центра математического моделирования и основоположник теории конечно-разностных схем в нашей стране. Его учебник [4] стал классическим. В последующих работах анализировались уже более узкие вопросы. В них рассматривались проблемы влияния шага по пространственным координатам на точность аппроксимации уравнений теплопроводности, устойчивости разностных уравнений теплопроводности и прочее [5; 6]. Однако рекомендации в этих работах достаточно общие и при несомненных положительных качествах не дают полного представления о том, как именно будут различаться решения, полученные при применении разных конечно-разностных схем.
В рамках настоящего научного исследования выполнено сравнение аналитического и численного решений (по нескольким конечно-разностным схемам) уравнения теплопроводности для выяснения того, какие параметры конечно-разностных схем являются оптимальными для моделирования процессов в двух средах: вода и лёд. Выбор уравнения теплопроводности связан с тем, что именно дифференциальные уравнения второго порядка составляют основу многих математических моделей развития ледников и процессов в подледниковых водоёмах [2; 7; 8].
Материалы и методы исследования
Постановка задачи
Для сравнения результатов будем решать одномерную задачу об изменении температуры θ с течением времени t в некотором безграничном, однородном и изотропном слое толщиной L с неизменным коэффициентом температуропроводности z. Его удобнее представить через a2, z≡a2. На обеих поверхностях (границах) слоя зададим граничные условия Дирихле (первого рода), которые предполагают неизменность температуры с течением времени на левой и правой границах θL и θR соответственно. Начальное распределение температуры также будем считать постоянным по всему слою и равным θ0. Совместим начало оси абсцисс с его левой границей, а правый будем ориентировать в сторону возрастания значений переменной x. Тогда математическая формулировка задачи примет вид:
,
,
,
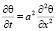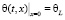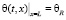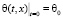. (1)
Для сравнения результатов, полученных при использовании разных конечно-разностных схем, граничные, а тем более начальные, условия принципиального значения не имеют и не нарушают общности решения, поскольку всегда могут быть сведены к ним путём замены переменных.
Аналитическое решение задачи теплопроводности
Задача в постановке (1) может быть решена аналитически, т.е. с получением точного решения, с которым и будут сравниваться все остальные. Для этого воспользуемся методом Фурье (разделения переменных). Однако он годится лишь при соблюдении нулевых граничных условий [9]. Чтобы этого достичь, введём новую переменную φ,
.
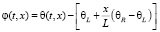В этом случае краевая задача (1) примет вид
, 
, 
.
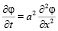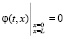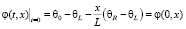Аналитическое решение этого уравнения известно [9]:
.
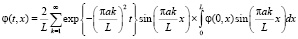Выполнив переход к прежней переменной θ, получим окончательное аналитическое решение уравнения (1) с ненулевыми начальными и граничными условиями:
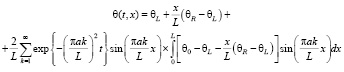. (2)
Несмотря на то что точное решение уравнения теплопроводности найдено, его нельзя представить в виде конечной комбинации элементарных функций. В этом смысле решение всё же является приближённым, но, при использовании большого количества членов разложения в ряд, оно практически совпадёт с точным. Таковым его и будем считать.
Численное решение с применением явной конечно-разностной схемы
Четырёхточечная явная конечно-разностная схема, шаблон которой представлен на рис. 1а, является наиболее простой численной реализацией уравнения теплопроводности. Если N – это количество точек по толщине слоя, в которых осуществляется поиск решения задачи, то расстояние Δx между ними при использовании равномерной сетки составляет Δx=L/(N-1). Тогда, возвращаясь к коэффициенту температуропроводности z, для вычисления значения температуры в n-й точке на j-м временном шаге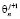 
может быть использовано соотношение
,
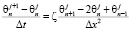где Δt – шаг по времени [6; 10]. Таким образом, искомая величина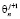 
:
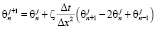. (3)
При всей простоте явной схемы (3) у неё имеется существенный недостаток. Он заключается в выполнении необходимого условия устойчивости – т.н. критерия Куранта. Его смысл заключается в том, что расчётная схема не может корректно обсчитывать распространение возмущения, которое в реальности происходит быстрее, чем предусмотрено вычислительной схемой. Таким образом, шаг по времени должен быть меньше некоторого порогового значения, иначе результаты расчётов становятся неверными либо получаются с большой ошибкой. Если число Куранта k, k≡2zΔt/Δx², то обсуждаемая схема является устойчивой при k<1 [6; 10]. Несмотря на этот нюанс, всё равно рассмотрим результаты, полученные при её использовании.
Рис. 1. Шаблоны конечно-разностных схем: явная (а), неявная (б), Кранка-Николсона (в)
Численное решение с применением неявной конечно-разностной схемы
Четырёхточечная неявная конечно-разностная схема, шаблон которой представлен на рис. 1б, является абсолютно устойчивой в n-й точке нашего столба воды на j-м временном шаге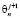 
. Уравнение теплопроводности при этом может быть записано следующим образом [6; 10]:
.
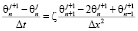Если решение в предыдущем случае получается путём последовательных вычислений вдоль оси абсцисс, то в этом оно является результатом решения системы, состоящей из N-2 уравнений (4) и двух граничных условий. То есть оно получается сразу на всём временном слое, а не постепенно. Если решать её классическим методом Гаусса, то потребуется значительный объём памяти и вычислений. Имеется более перспективный подход, называемый методом прогонки [6; 10]. Неявная разностная схема абсолютно устойчива [6; 10; 11], т.е. решение имеется вне зависимости от числа Куранта. Это, безусловно, является важным достоинством неявной конечно-разностной схемы.
Численное решение с применением конечно-разностной схемы Кранка-Николсона
Рассмотрим ещё одну распространённую безусловно устойчивую шеститочечную конечно-разностную схему Кранка-Николсона. Её шаблон приведён на рис. 1в. Эта схема относится к классу схем с весами. Её идея заключается в более точном расчёте производных по плановым координатам, что, как следствие, при прочих равных условиях позволяет получить более точное решение [6; 10; 11]. Следуя [10], перепишем уравнение теплопроводности (1) в виде
,
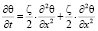а каждое из слагаемых правой части представим конечно-разностной схемой. При этом первое будем рассчитывать на временном слое j, а другое – на слое j+1. Тогда
.
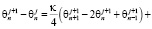
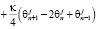Далее используется метод прогонки.
Результаты исследования и их обсуждение
Сравним результаты моделирования, выполненного с применением всех трёх рассмотренных выше конечно-разностных схем с точным аналитическим решением (2). Поскольку задача исследования заключается в выяснении оптимальных параметров для моделирования процессов в ледниках и в подледниковых водоёмах, то для определённости будем считать, что рассматриваемая среда – вода с коэффициентом температуропроводности ζ=1,351×10⁻⁷ м²/с. Пусть толщина слоя составляет 25 м. В начальный момент времени q0=10 °C; граничные условия постоянны: qL=20 °C и qR=0 °C. Начальное распределение показано на рис. 2 (кривая 1).
Обратимся к рис. 3. На нём показаны графики среднеквадратичных отклонений σ численных решений от точных при различных интервалах времени Δt и постоянном количестве точек дискретизации N по толщине слоя, N=500. Это соответствует интервалу дискретизации Δx=50 мм. Есл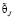и 
и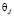 
– аналитическое и численное решение в точке J соответственно, то σ может быть получено по известному статистическому соотношению
.
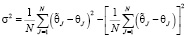Как следует из представленных графиков, величина σ для первых расчётных значений достаточно высока. Затем она стремительно убывает по обратному экспоненциальному закону.
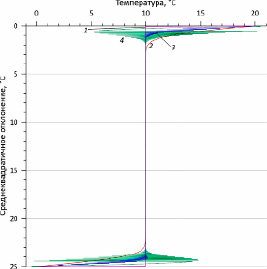
Рис. 2. Примеры модельных распределений температуры в слое воды толщиной 25 м, Δx=50 мм: 1 – начальное распределение; 2 – распределение температуры, смоделированное через 30 суток для схемы Кранка-Николсона при Δt=10 мин.; 3 – распределение температуры, смоделированное через 7 сут. 18 час. 40 мин. для явной схемы при Δt=2 час. 40 мин. (k=1,93); 4 – то же, через 11 сут. 16 час
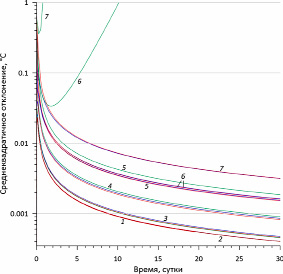
Рис. 3. Сравнение результатов моделирования для воды при Δx=50 мм: 1 – Δt=10 с, k=0,0010; 2 – Δt=1 мин., k=0,0064; 3 – Δt=10 мин., k=0,0645; 4 – Δt=1 час, k=0,3875; 5 – Δt=2 часа 30 мин., k=0,9690; 6 – Δt=2 часа 40 мин., k=1,0336; 7 – Δt=6 часов, k=2,326. Синим цветом показаны кривые, построенные при использовании неявной конечно-разностной схемы, зелёным – явной, красным – Кранка-Николсона
Это связано с тем, что распределение температуры в начальный момент времени представляет собой сумму двух функций Хевисайда (рис. 2). Они, как известно, очень плохо описываются разложением в ряд Фурье, что требуется для аналитического решения (2), поскольку для практической реализации ряд не может состоять из бесконечного количества членов. Для построения решения авторы использовали разложение в ряд по 500 гармоникам. Таким образом, большие ошибки на этом временном интервале обусловлены исключительно недостатками описания аналитического решения. Но уже буквально после первых расчётных циклов начальное распределение чуть сглаживается, и численная реализация аналитического решения постепенно приближается к истинному. При этом величина ошибки σ уменьшается сразу примерно на полтора порядка (рис. 3). Судя по тому, что далее наблюдается вполне закономерная зависимость σ от числа Куранта, вклад ошибки реализации аналитического решения резко снижается, а ошибки интересующего нас численного решения – возрастает. В качестве примера на рис. 2 показано распределение температуры, наблюдаемое через 30 суток для схемы Кранка-Николсона при Δt= 10 мин. (кривая 2). Остальные решения не показаны, поскольку все они визуально совпадают друг с другом.
Расчётные кривые (рис. 3) показывают, что при использовании любой рассмотренной конечно-разностной схемы точность вычислений повышается с уменьшением Δt (и соответственным уменьшением числа Куранта). Это вполне закономерно, поскольку чем меньше интервал дискретизации по времени и по пространству, тем точнее вычисляются производные и, как следствие, точнее производятся расчёты посредством конечно-разностных схем. Исключение составляет явная схема, применение которой при числах Куранта k>1 приводит к неустойчивому решению. Оно выражается в появлении гармонических флуктуаций, амплитуда которых постепенно нарастает. Скорость этого процесса возрастает с увеличением k. В качестве примера неустойчивое решение показано на рис. 2 (кривая 3). Оно рассчитано при Δt = 2 час. 40 мин. (что соответствует k= 1,93) и получено через 7 сут. 18 час. 40 мин. от начала моделирования. Кривая 4 на том же рисунке показывает результат моделирования через 11 сут. 16 час. Как видно из представленных графиков, амплитуда вариаций достаточно быстро возрастает и в конечном итоге становится бесконечно большой. Увеличение флуктуаций сопровождается резким ростом величины общей ошибки σ, что наглядно демонстрируется на рис. 3 (кривые 6 и 7).
Если фиксировать N (т.е. Δx), то по мере роста числа Куранта убывание точности (т.е. рост σ) экспоненциально возрастает. Это наглядно демонстрируется группой графиков 1 на рис. 4. Таким образом, значения k>1 хоть и не приводят к неустойчивому решению для неявной конечно-разностной схемы и схемы Кранка-Николсона, но делают результат менее точным. В частности, при увеличении числа Куранта с 1 до 10 ошибка σ возрастает примерно с 0,004 °C до 0,03 °C. При этом максимальные отклонения могут превышать эти значения на порядок и более. Это уже неприемлемо, поскольку указанные величины превышают точностные характеристики датчиков термокос [12].
Погрешность вычислений, достигаемая при k=0,06, составляет менее 0,001°C, что вполне приемлемо для любых расчётов. Кроме того, этому значению k для воды соответствует интервал Δt=10 мин. С позиций сбора термометрических данных этот интервал регистрации также оптимален, поскольку позволяет отследить с хорошей точностью не только сезонные, но и суточные колебания. С другой стороны, дальнейшее уменьшение k, а, следовательно, Δt, безусловно, улучшит результат (рис. 3, 4). Однако это повлечёт за собой существенное увеличение времени счёта. С другой стороны, графики на тех же самых рисунках показывают, что дальнейшее уменьшение интервала Δt не оправдывает достигаемой при этом точности вычислений. Таким образом, k≈0,05 можно считать оптимальным параметром для моделирования задач тепломассопереноса применительно к гидрологическим и гляциологическим расчётам.
Второй достаточно известный вывод, который следует из представленных рисунков, заключается в том, что конечно-разностная схема Кранка-Николсона в целом точнее неявной схемы. Однако расчёты показывают, что при k<0,1 явная конечно-разностная схема становится более точной, хоть и ненамного. При k<0,01 различий между всеми схемами практически не наблюдается.
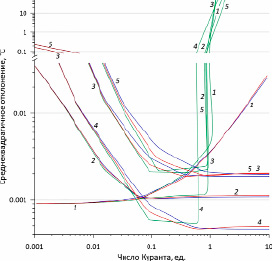
Рис. 4. Сравнение ошибок между аналитическим решением и решением по разным конечно-разностным схемам для сред вода и лёд на момент времени, равный 10 дням. Вода: 1 – Δx=50 мм, 2 – Δt=10 мин., 3 – Δt=1 час. Лёд: 4 – Δt=10 мин., 5 – Δt=1 час. Синим цветом показаны кривые, построенные при использовании неявной конечно-разностной схемы, зелёным – явной, красным – Кранка-Николсона
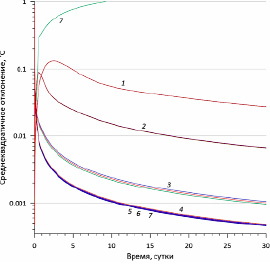
Рис. 5. Сравнение результатов моделирования для воды при Δt=10 мин.: 1 – Δx=510,0 мм, k=0,000622755; 2 – Δx=252,5 мм, k=0,00254; 3 – Δx=100,4 мм, k=0,01608; 4 – Δx=50,1 мм, k=0,0646; 5 – Δx=33,4 мм, k=0,1455; 6 – Δx=25,0 мм, k=0,2589; 7 – Δx=12,5 мм, k=1,036. Синим цветом показаны кривые, построенные при использовании неявной конечно-разностной схемы, зелёным – явной, красным – Кранка-Николсона
Поскольку на число Куранта влияет не только Δt, но и Δx, проанализируем изменение этого параметра на точность получаемого результата. Для определённости сделаем это при Δt=10 мин., так как именно этому интервалу времени соответствует оптимальное число Куранта, согласно предыдущим оценкам. Зависимость погрешности вычислений σ от расчётного времени для воды показана на рис. 5. Как следует из представленных графиков, в данном случае наблюдается обратная закономерность: рост числа Куранта приводит к уменьшению погрешности. В целом это понятно, поскольку в данном случае происходит уменьшение интервала дискретизации по расстоянию, что приводит к улучшению точности определения производной по плановым координатам. Однако, начиная со значений k=0,06, значимого уменьшения σ не наблюдается (серия кривых 4, 5, 6 и 7). При этом, как и в предыдущем случае, при k>1 явная конечно-разностная схема становится неустойчивой. Таким образом, предложенную выше величину k≈0,05 можно считать оптимальной и в этом случае. На серии графиков 2 (рис. 4) представлено аналогичное сравнение точности результатов моделирования (величины σ), выполненного при использовании всех трёх конечно-разностных схем с аналитическим решением. Расчёты проведены при постоянном значении Δt=10 мин. Как следует из представленных графиков, наиболее точным решением (при условии его устойчивости) является то, которое получено при использовании явной схемы. Затем следует схема Кранка-Николсона и, наконец, неявная конечно-разностная схема. Приемлемая точность достигается также начиная с k≈0,05.
Попробуем увеличить интервал дискретизации по времени Δt с 10 минут до 1 часа, т.е. чуть ухудшим точность определения первой производной по времени и построим аналогичные графики. Они показаны серией кривых 3 на рис. 4. Предыдущая тенденция сохранилась: точность возрастает с ростом числа Куранта. Однако при этом закономерно возросла ошибка. При k>0,3 рост составил около 10%; при меньших значениях он гораздо больше, и при k<0,1 точность построений уже становится слишком низкой для каких-либо серьёзных оценок.
Поскольку планируется также моделирование субгляциальных гляциологических процессов, то логично произвести оценки не только для воды, но и для льда. Они представлены сериями графиков 4 на рис. 4. Расчёты выполнены при аналогичных параметрах: толщина среды 25 м, Δt=10 мин., ζ=1,184×10⁻⁶ м²/с. Граничные и начальные условия уменьшены на 20 °C. Этим сохраняются относительные изменения, т.е. qL= -20 °C, qR= 0 °C, q0= -10 °C. Таким образом, эти построения по соотношению Δt и Δx аналогичны серии кривых 2 (рис. 4). Однако коэффициент температуропроводности ζ льда почти на порядок больше, чем у воды. Из графиков видно, что ход кривых 2 и 4 в целом сходный, и при k чуть менее 0,1 точностные характеристики серий становятся практически одинаковыми (кривые обеих серий пересекаются). При дальнейшем росте k точность построений для льда избыточно повышается и становится менее 0,001 °C. По мере приближения к значению k=1 точность построений для явной конечно-разностной схемы падает. При значениях k, близких к 0,5, её погрешность резко увеличивается, а затем решение становится неустойчивым.
На том же рисунке сериями кривых 5 показаны результаты аналогичных расчётов, полученные при Δt=1 час по аналогии с серией кривых 3 для воды. Несмотря на то что ζ сред отличается почти на порядок, кривые при малых k различаются не сильно. При k>1 эти серии кривых практически совпадают, за исключением нестабильных решений для явной конечно-разностной схемы.
Заключение
Для решения задач, которые основаны на уравнениях матфизики, параметры моделирования выбираются исходя из ожидаемых результатов. При этом современные модели, как правило, достаточно сложны и требуют значительных ресурсов и времени для расчётов. В этой связи выбор параметров для их минимизации с сохранением разумной точности является важной практической необходимостью, поскольку если точность избыточна, то ресурсы расходуются неоправданно, а скорость вычислений падает.
Настоящее исследование показало, что для достижения приемлемой точности, которая оправдана с позиций технических характеристик термодатчиков, имеет смысл задавать интервалы дискретизации по времени от 10 минут до одного часа и подбирать количество точек дискретизации по плановым координатам таким образом, чтобы число Куранта лежало в пределах от 0,05 до 0,1. Полученные расчёты показали, что при малых значениях числа Куранта точность явной конечно-разностной схемы выше остальных. Этот результат стал неожиданным для авторов. Следующей по точностным характеристикам идёт конечно-разностная схема Кранка-Николсона. Она более предпочтительна по сравнению с неявной схемой, но при указанных параметрах это не имеет большого значения. В принципе, если число Куранта не превысит значение 0,1, то вполне допустимо использование явной конечно-разностной схемы. Это существенно сэкономит ресурсы и увеличит время счёта. Вышеизложенное применимо к средам, коэффициенты температуропроводности которых находятся в интервале значений от 1×10⁻⁷ до 2×10⁻⁶ м²/с, что включает в себя лёд и воду.
Работа выполнена при финансовой поддержке Российского научного фонда (РНФ) в рамках проекта № 22-27-00266 «Разработка математической модели развития ледникового покрова с последующим применением для описания субгляциальных гидрологических процессов в районе подледникового озера Восток, Восточная Антарктида».