Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Гидравлический разрыв пласта в настоящее время является одним из самых эффективных методов повышения нефтеотдачи, и при использовании этой операции рассматривают качество расклинивающего материала для заполнения трещины гидроразрыва, такие как диаметр и способ укладки частиц, их отсортированность, проницаемость трещины с расклинивающим материалом. Перед применением данного метода для прогноза желательно иметь значительное количество нефтепромысловых данных и сопутствующих исследований, чтобы снизить риски недостаточной эффективности проведения метода [1; 2].

Цель исследования – по результатам исследований параметров фильтрации газа на установке «Дарсиметр» через искусственные образцы с расклинивающим материалом, моделирующие трещину гидроразрыва пласта, установить вид нелинейной степенной зависимости между градиентом давления и расходом газа; исследования провести на цилиндрических искусственных образцах, вмещающих пропант или песок с заданным размером зерен, и в искусственных образцах в виде щелей с расклинивающим материалом; рассчитать по образцам искусственных трещин проницаемость.

Материалы и методы исследования

В настоящей статье изучались параметры фильтрации: расход газа, градиент давления и проницаемость на насыпных моделях с расклинивающим материалом: пропантом, кварцевым песком размером зерен от 40 до 500 мкм.

Установка по определению газопроницаемости образцов пород

Исследования провести на установке «Дарсиметр» (рисунок). Определялся вид степенной зависимости между расходом газа и градиентом давления в интервале от 0,1 до 1,6 атм. Изучение нелинейной фильтрации можно проводить по уравнению Форхгеймера или с помощью степенных зависимостей, используя искусственные нейронные сети и множественные регрессионные модели [3–6].

Дарсиметр

Известно, что нелинейный закон фильтрации газа может быть выражен как скорость фильтрации v в зависимости от градиента давления dp / dL [7]:

,

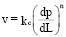где n принимает значение в пределах .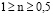

Численные значения n и kc в каждом случае определяются из опытов. В настоящем исследовании уточнялось изменение показателей n и kc в зависимости от изменения градиента давления. В опытах с грубозернистым песком при фильтрации жидкости была выведена зависимость

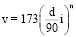[7],

где d – диаметр зерен, а i – гидравлический уклон или градиент давления dp / dL, отличающийся от i на постоянный множитель удельный вес жидкости.

Выявлено, что с увеличением диаметра зерен величина показателя степени уменьшается. В наших исследованиях, при фильтрации газа, предполагалось проверить, справедливо ли будет изменение показателя степени, при изменении диаметра зерен расклинивающего материала. Для расчета проницаемости использовались выражения

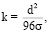[7] (1)

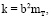[2] (2)

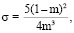
где b – раскрытость щели,

mТ – трещинная пористость,

m – пористость.

Проницаемость в искусственных образцах, наполненных зернами пропанта, зависит от величины угла Θ при различном расположении зерен. Крайние конфигурации соответствуют теснейшему расположению зерен при Θ = 60° и свободному при Θ = 90°.

Для исследований применялся цилиндрический искусственный образец из оргстекла с внутренним отверстием, заполняемым исследуемым материалом и уплотняемым с торцов. А также использовался искусственный образец щели.

Таблица 1

Степенная зависимость расхода газа от перепада давления Q = F(Δp), Q*μ/s = F(p/l), k, Re для зерен разного размера пропанта и песка

Исследуемый образец представлял собой полоску с размещенным на клее веществом пропанта заданной фракции в один слой. Полоска укреплялась в щели вплотную по ее раскрытости, равной диаметру зерен исследуемого материала и толщине подложки. Также исследовался образец пленки с пропантом и с некоторым дополнительным раскрытием. Это был образец пленки с пропантом диаметром 180 мкм и дополнительной раскрытостью 75 мкм. Расклинивающий материал представлял собой пропант марки Боровичи, который был рассеян на фракции от 212 до 300 мкм, более 300 мкм и более 500 мкм. Также использовались смесь 50 % естественного образца пропанта и 50 % фракции менее 63 мкм, а также кварцевый песок фракций 40, 63, 80, 125, 150, 180 мкм.

Результаты исследования и их обсуждение

Для определения погрешностей исследования проведены измерения расхода газа при давлении 1 атм для 15 перенабивок образца. Математическое ожидание расхода составило q=5,6 *10^-5 м3, среднее квадратичное отклонение 1,21 *10-5, коэффициент вариации 0,21.

Рассмотрим полученные результаты (табл. 1). В степенной зависимости Q = f(p) при увеличении диаметра зерен от 40 до 500 мкм значение степени снижается от 0,905 до 0,53, а в свободном множителе или коэффициенте пропорциональности значение степени снижается от -12 до -7. Для зависимостей с малым диаметром 40, 63 мкм графики зависимостей Q = f(p) при p = 0,1–1,7 атм аппроксимируются прямыми линиями. Уравнение прямой линии для зерен 40 мкм y = 2*10-10x+2*10-6. Числа Рейнольдса для этих данных не выше критического значения по Щелкачеву. Для опытов с расклинивающим материалом с d = 40, 63, 80, 106 мкм рассчитывались значения коэффициента проницаемости с учетом погрешности из-за отклонения реального закона фильтрации от линейного закона Дарси (табл. 1). Коэффициент пропорциональности Kc отличается от коэффициента проницаемости k приблизительно в 3 раза для образцов с d = 40, 63 мкм. И эти параметры отличаются в 10 раз для образцов с d = 80 мкм. Таким образом, зависимости для зерен с d = 40, 63 мкм близки к линейным. Использование для расчетов закона Дарси в таких случаях является некорректным. При увеличении диаметра зерна материала на пленках в искусственных щелях от 100 до 180 мкм показатель степени при x снижается от 0,77 до 0,64.

Таблица 2

Законы фильтрации через цилиндрические образцы

Рассмотрим полученные законы фильтрации через цилиндрические образцы с расклинивающим материалом разного диаметра зерен при трех режимах перепада давления (табл. 2). 1 режим приближенно от 1 до 1,7 атм, 2 режим приближенно от 0,5 до 1 атм, 3 режим от 0,1 до 0,5 атм (табл. 2). В таблице показаны степенные зависимости Q = f(p) и Qμ/s = F(p/l).

При снижении перепада давления для зерен фракций от 212 до 300 мкм, более 300 мкм и более 500 мкм показатель степени при x возрастает. Меньший показатель степени при x для зерен с самым большим диаметром d = 500 мкм при перепаде давления 1–1,7 атм составил 0,307. Для диаметра зерен с d фракция от 212 до 300 мкм показатель степени при x для диапазона Δp = 1–1,7 атм составил 0,42, для диапазона Δp = 0,5–1 атм показатель степени – 0,49 для диапазона Δp = 0,1–0,5 атм показатель степени – 0,6. Зависимости, полученные по общему перепаду давления от 0,1 до 1,7 атм, отличаются от зависимостей, полученных при более узких перепадах: 0,1–0,5; 0,5–1; 1–1,7 атм – и являются менее точными.

Таблица 3

Законы фильтрации через образцы искусственных щелей

Рассмотрим полученные законы фильтрации через образцы искусственных щелей с расклинивающим материалом разного диаметра зерен и без расклинивающего материала (табл. 3).

Таблица 4

Рассчитанная проницаемость по искусственным щелям

При увеличении диаметра зерна от 100 до 180 мкм на материале пленок в искусственных щелях показатель степени при x снижается от 0,77 до 0,64, а степень при свободном сомножителе изменяется от -8 до -7. Для открытой щели 75 мкм при диапазоне давления p = 1,04–0,105 атм зависимость q = f(p) составила 3*10-10x0,81, однако для диапазона 0,392–1,04 атм зависимость имеет вид 6*10-10x0,77. Эти изменения вида зависимости при изменении диапазона давления подобны цилиндрическим образцам. Щель 75+180 состоит из пленки с зернами 180 мкм и параллельного пространства из щели с раскрытостью 75 мкм. По обеим частям этой композитной щели идут два потока газа пропорционально их проницаемостям, и суммарный поток рассчитывается по средней проницаемости щели. Вид зависимости для этой щели 2*10-7x0,606. Вид зависимости подобен для щели c расклинивающим материалом 180 мкм, чем для открытой щели 75 мкм. И имеет вид 3*10-8x0,64. Щель 150 мкм исследовалась при диапазоне давления 0,065–0,3 атм. Разделив общий интервал на 2 подынтервала 0,065–0,175 атм и 0,175–0,3 атм, нашли две зависимости, значительно отличающиеся по показателю степени при перепаде давления -7*10-10x0,87 и 2*10-11x1,14. Это связано, вероятно, со значительной раскрытостью щели и с проявлением нелинейной фильтрации газа. Для цилиндрического образца и щели для зерен 180 мкм получены практически идентичные законы фильтрации, и 100 мкм показало практически идентичные фильтрации законы: 2*10-8 x0,65 для цилиндрического образца и 3*10-8x0,64 для искусственной щели. Несколько различимы законы для образцов с зернами d = 100 мкм.

Это связано с различной упаковкой зерен при укладке в образцы – от возможных крайних конфигураций, соответствующих теснейшему расположению зерен при Θ = 60° и свободному при Θ = 90°.

Проницаемость для щели 180 мкм составила 77Д и для щели 100 мкм 24Д (табл. 4). Для щели 75 мкм проницаемость по формуле (2) cоставила 466 Д а для щели 150 мкм – 1867 Д. Для щели из двух компонентов 180 + 75 расчет производился по известной зависимости для нахождения средней проницаемости пласта, состоящего из двух пропластков разной проницаемости и мощности, и в результате суммарная проницаемость оказалась 216 Д. Между показателем степени зависимости и диаметром зерен расклинивающего материала от 40 до 500 мкм получена связь n = 5,67d0,45 при величине достоверности аппроксимации R2 = 0,89.

Заключение

На искусственных образцах, моделирующих трещину гидроразрыва с расклинивающим материалом пропанта Боровичи со средним диаметром зерен от 250–600 мкм, и фракциях кварцевого песка с диаметром от 40 до 180 мкм установлены степенные зависимости расхода газа от перепада давления и зависимости скорости фильтрации от градиента давления. Установленные зависимости

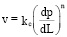
имеют показатель степени n = 0,92–0,31, снижающийся при увеличении диаметра зерен от 40 до 600 мкм. В пределах каждого диапазона перепада давлений от 0,1 до 1,7 атм для опыта с выбранной фракцией показатель степени n снижается на участке повышенных перепадов давлений от 1 до 1,7 атм. Коэффициент пропорциональности Kс для фракций пропанта изменяется от 4*10-9 до 3*10-7. Коэффициент пропорциональности при диаметре зерен 40 мкм при фильтрации газа по закону близкому к линейному принимает значение 6*10-12x0,92 и больше коэффициента проницаемости вычисленного по закону Дарси приблизительно в 3 раза. Полученные результаты исследований возможно использовать для оценки качества расклинивающего материала в трещине гидроразрыва пласта.