Процесс извлечения данных из результатов полевых гравитационных и магнитных наблюдений и экспериментов весьма трудоемок. Современные приборы способны обеспечивать высокую точность определения значений исследуемых свойств и параметров пород. Но теория гравиразведки, а именно интерпретации потенциальных полей, не вполне успевает за развитием техники [1]. Данные, полученные с приборов, представляют собой набор карт и графиков, содержащих материал о составе, свойствах пород и геологическом строении исследуемого участка. Стоит отметить, что указанные наборы данных сами по себе нельзя назвать полной геологической информацией. После получения наборов данных начинается процесс интерпретации, состоящей из аналитических и синтетических процедур. Интерпретация геофизических полей позволяет выяснить природу аномалий, связать аномалии с геологическими процессами, которые, в свою очередь, привели к образованию наблюдаемых объектов. Также интерпретация аномалий позволяет определить размеры и глубины залегания источников [2]. Автором предлагается аналитический метод, основанный на математических методах обработки данных [3, 4]. Разработанный метод позволяет сократить объемы математических вычислений, тем самым решить упомянутую проблему отставания теории гравиразведки от возможностей современной аппаратуры [1]. На основе существующей теоретической базы о гравитационном и магнитном потенциалах можно утверждать, что процесс интерпретации гравитационной или магнитной аномалии более эффективен при анализе исходного поля совместно с производными: горизонтальными, вертикальными, первого или второго порядков. Природа источников аномалии может быть различной в зависимости от физических свойств, например намагниченности, глубины залегания, формы, размеров тел. Обратная задача гравиразведки решается для уточнения геологического строения разреза пород [5]. Определение формы эталонного тела перед началом процесса интерпретации оптимизирует и значительно уменьшает неоднозначность решения обратной задачи гравиразведки. Однозначное решение обратной задачи возможно в некоторых случаях, когда фактор одновременного влияния нескольких источников гравитационных аномалий исключается из математических расчетов [6], например в случае, если определяются параметры уступа на поверхности слоя пород или известна избыточная плотность рельефа местности. В данной работе рассматривается способ применения эталонного тела для повышения однозначности решения обратной задачи в сложных геологических средах и получения достоверной информации о местоположении источников аномального поля.
Цель исследования – анализ возможностей применения эталонного тела для решения обратной задачи магниторазведки и гравиразведки.
Материалы и методы исследования
В качестве материалов исследования применяется физико-геологическая модель нефтеносной структуры, приведенная в работе [7] профессора С.А. Серкерова. Для совершенствования существующих методов интерпретации аномалий силы тяжести разработаны двухмерные способы интерпретации гравимагнитных аномалий, чувствительных к форме источников полей. Ниже рассмотрены разработанные способы, в которых используются значения взаимно-обратных функций нормированных аномалий – значения горизонтальных координат Ха, Х′а, определяемые равенствами:
Ха = f(VZ(x)H), (1)
Х′а = g(VXZ(x)H), (2)
где VZ(x)H , VXZ(x)H – нормированные значения гравитационной аномалии и ее первой производной. На рисунках 1а, 1б представлены графики изменений упомянутых значений:
C2 = XГП / ХМЛ и C2 = XВП / ХМЛ , (3)
где XГП , XВП , ХМЛ – значения взаимно-обратных функций Ха бесконечных горизонтальной, вертикальной полос и материальной линии, рассчитанных из формул, приведенных в [4] при различных значениях а.
Параметры кривых: значения l / h и Δh / h, где l – ширина полосы, h – глубина залегания; Δh = h2 – h1 где h1 и h2 – глубины залегания верхней и нижней кромок полосы. Кривые с параметрами 0 в обоих графиках соответствуют случаю, когда интерпретируемая кривая является аномалией от тела той же формы, что и эталонное, а именно от бесконечной горизонтальной материальной линии. Указанные кривые во всех точках принимают постоянное значение, равное 1.
Сравним графики, представленные на рисунках 2а, 2б. Изменение значений С2 для аномалий от бесконечных материальных горизонтальных и вертикальных полос имеют разные формы: в первом случае они являются возрастающими, во втором – убывающими. Этот признак, то есть разные формы кривых, позволяет относительно легко определить формы тела, а затем и их параметры l / h и Δh / h1 (по той же методике, что и по кривым С1) [4].
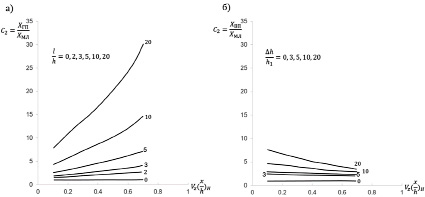
Рис. 1. кривые С2: а – бесконечная горизонтальная полоса; б – бесконечная вертикальная полоса
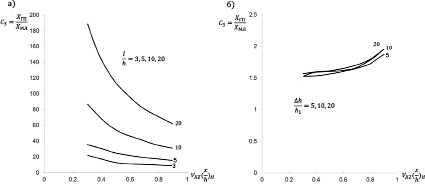
Рис. 2. Кривые С3: а – горизонтальная полоса; б – вертикальная полоса
На рисунке 2 приведены кривые изменения значений функции:
C3 = X′ГП / Х′МЛ и C3 = X′ВП / Х′МЛ,
(случаи а, б соответственно) (4)
где X′ГП, X′ВП, Х′МЛ – рассчитанные в статье [4] значения взаимно-обратных функций для нормированной горизонтальной производной исходной аномалии VXZ , см. формулу (2). В этом случае кривые для разных аномалий (случаи а, б) отличаются разной формой, что также можно использовать для определения формы тела. Параметрами кривых также являются отношения l / h и Δh / h1.
По кривым рисунка 2а можно легко определить параметры l / h. В случае, представленном на рисунке 2б, параметр Δh / h1 можно определить только в благоприятных случаях, поскольку кривые, соответствующие разным параметрам, мало отличаются друг от друга.
В случае применения эталонного тела нужно знать также нормированные значения аномалий. Для нахождения аномалий определяется глубина залегания указанного эталонного тела. В соответствии с ранее выполненными автором расчетами [4], глубина залегания полосы определяется значениями h и h1, которые можно получить посредством спектральных способов, изложенных в работе [7], например по угловому коэффициенту асимптоты, проведенной к точкам ln|S(ω)| в области высоких частот, где S(ω) – спектр аномалии. Зная h или h1, можно определить VZ(x)H по следующей формуле:
VZ(x)H = h2 / (h2 + x2), (5)
Результаты исследования и их обсуждение
Разработанные аналитические способы позволяют интерпретировать аномалию силы тяжести от нефтегазоносной структуры. Рассмотрим пример, представленный на рисунке 3.
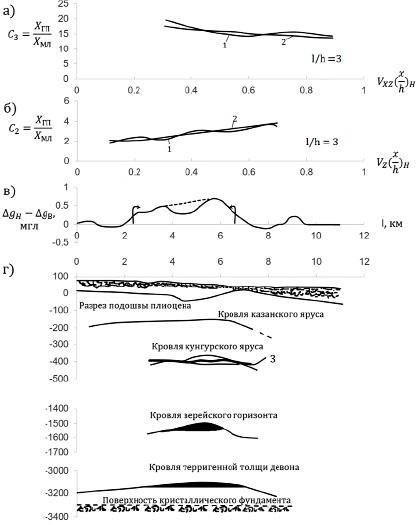
Рис. 3. Интерпретация гравитационной аномалии
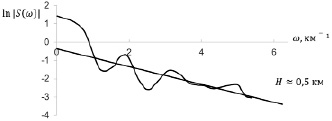
Рис. 4. График ln|S(ω)| аномалии силы тяжести
На рисунке 3в представлена кривая остаточной аномалии нефтегазоносной структуры. Поверхностные неоднородности представлены здесь пунктирной линией. По этой кривой были найдены значения первой производной аномалии VXZ. КривыеVZ и VXZ были нормированы, после чего определены значения горизонтальных координат Ха и Х′а. По этим значениям были построены кривые С2 и С3, представленные на рисунках 3а и 3б (кривые под цифрами 1 и 2). Эти кривые по своим формам подходят к кривым рисунка 1а и рисунка 2а. Следовательно, рассматриваемую аномалию можно аппроксимировать бесконечной горизонтальной полосой. Кривые, обозначенные цифрами 1 и 2, на обоих графиках лучше всего совпадают с линиями, соответствующими параметру l / h = 3.
Значения h можно определить из графика ln|S(ω)| (рис. 4) или из выражений для горизонтальной полосы:
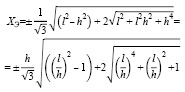 (6)
(6)
где ХЭ – абсциссы экстремумов VXZ, Х1/2 – абсциссы точек с координатой, равной 1/2Δ



