Для изучения кинематических характеристик современной геодинамики, прогноза сейсмических событий, контроля сдвижений земной поверхности на разрабатываемых месторождениях углеводородов и подземных хранилищах газа, а также для решения других научно-практических задач геофизики и инженерной геодезии создаются сети высокоточного нивелирования на прогностических, изыскательских и техногенных геодинамических полигонах [1; 2]. При этом в сетях нивелирования геодинамических полигонов через определенные промежутки времени выполняется повторно высокоточное нивелирование I и II классов точности.
В настоящее время на геодинамических полигонах нивелирование выполняется с применением высокоточных оптических нивелиров в комплекте со штриховыми инварными рейками, имеющими основную и дополнительную шкалы, и чаще цифровыми нивелирами, укомплектованными кодовыми инварными рейками, имеющими лишь «одну шкалу». Приборная точность таких нивелиров позволяет выполнять нивелирование в «лабораторных условиях» с точностями 0,5 мм/км (II класс) и 0,3 мм/км (I класс). В действительности точность нивелирования I и II классов, выполняемого в полевых условиях, зависит от совокупного влияния многих внешних факторов (температуры и влажности воздуха, вида и состояния почвогрунтов, стабильности угла наклона нивелира, гидротермических движений земной поверхности и других) [3-5] на процесс измерения превышений на нивелирных станциях, которое проявляется в случайных и систематических погрешностях нивелирования [6; 7].
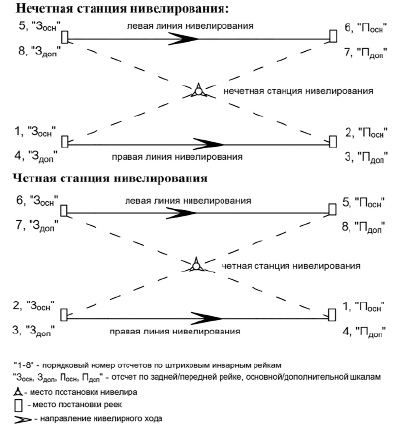
Рис. 1. Реализация оптическим высокоточным нивелиром программы нивелирования I класса на станции нивелирного хода
Целью исследования является обоснование возможности замены нивелирования I класса нивелированием II класса (менее громоздким, затратным и более высокопроизводительным). Очевидно, что возможность такой замены требует теоретического обоснования с позиции повышения жесткости допусков на расхождения измеренных превышений и количества приемов (горизонтов прибора) при измерениях. Если такая замена возможна, то также необходимо определить дополнительные условия использования замены.
Материалы и методы исследования
Современные технологии нивелирования I и II классов, использующие оптические нивелиры, позволяют путем применения специальных программ нивелирования на станции [6; 7] исключать или ослаблять до требуемых пределов влияние внешних факторов на результаты измерения превышений. Реализация таких программ (рис. 1) возможна при включении в них серии отсчетов по основным (Зосн, Посн) и дополнительным (Здоп, Пдоп) шкалам инварных реек при нивелировании по правой и левой линиям нивелирования [6; 7], а именно: Зосн(прав), Посн(прав), Пдоп(прав), Здоп(прав), и Зосн(лев), Посн(лев), Пдоп(лев), Здоп(лев). Выполнение программ позволяет также осуществлять контроль качества измерения превышения на четных и нечетных станциях путем соблюдения допусков на разности превышений di, установленных нормативными документами [6-8].
При нивелировании высокоточными цифровыми нивелирами используются кодовые инварные рейки с «одной» шкалой, что исключает возможность применения программ на нивелирной станции, рекомендованных нормативными материалами [6; 7] при применении оптических нивелиров (рис. 2).
Фактически программы для нивелирования цифровым нивелиром на станции при нивелировании I и II классов состоят из измерений превышения между кодовыми рейками соответственно при четырех и двух горизонтах нивелира, что позволяет контролировать измерение превышений по контрольным разностям di.
Результаты исследования и их обсуждение
Сначала покажем, что если при больших допусках все n наблюдений практически являются независимыми и дисперсия среднего арифметического в n раз меньше дисперсии одного наблюдения, то при малых допусках мы имеем дело фактически с одним наблюдением, и дисперсия среднего арифметического наблюдений практически равна дисперсии одного, отдельно взятого наблюдения [9; 10].
Пусть имеется n независимых наблюдений: f(x) – плотность распределения одного, независимо от остальных проведенного наблюдения; F(x) – функция распределения независимо проведенного наблюдения. Предположим следующую схему наложения допусков на ряд независимых наблюдений, проводимых n приемами.
Проводим наблюдение первым приемом, получим значение x1 случайной величины x. Пусть xi – результат наблюдения i приемом, тогда должны быть выполнены включения:
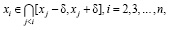(1)
где δ – величина допуска. Затем вычисляется арифметическая средняя:
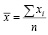(2)
Если же включения (1) нарушаются при некотором i, то результаты наблюдений x1, … , xi-1 отбраковываются и снова выполняется вся процедура получения результатов измерений n приемами (при разных горизонтах).
Далее без ограничения общности, для простоты выкладок, будем считать, что измеримая величина равна нулю. Тогда M(x1) = 0, а при отсутствии допусков и M(x2) = … = M(xn) = 0.
При наличии допусков возникают несимметричные усечения распределения F(x) случайных величин xi (при i ∈ [1; n]), зависящие от x1, x2, … …, xi-1. Более точно можно считать, что случайные величины xi имеют условные плотности распределения fiδ, где fiδ(x) = f(x) [9]:
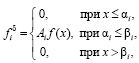, (3)
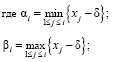
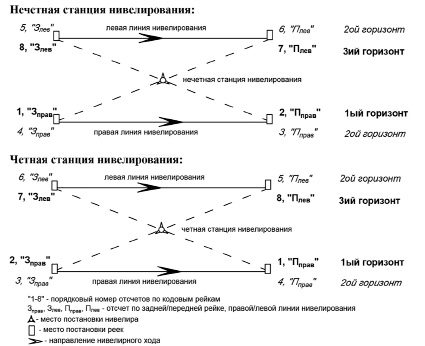
Рис. 2. Реализация цифровым высокоточным нивелиром программы
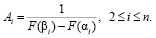
Отметим, что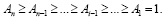 
Тогда совместная плотность распределения f(x1,…,xn) системы случайных величин (x1,…,xn) имеет вид:
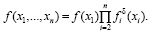(4)
Вычислим функцию распределения Fxδ(r) случайной величины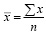 
по формуле [9]:
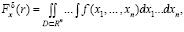(5)
где область D в n-мерном пространстве Rn задается неравенством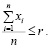 
После перехода к n-кратному повторному интегралу получим:
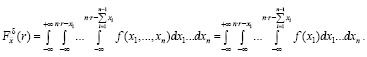(6)
С целью упрощения математических выкладок ограничимся случаем двух измерений превышения на станции, т.е. пусть n = 2, тогда: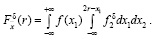 
Продифференцируем Fx(r) по верхнему пределу r, получим:
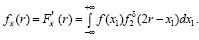. (7)
Далее вычислим [9]:
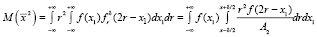(8)
В (8) мы учли, что вне интеграла x1 – δ/2 ≤ r ≤ x1 + δ/2 функция f2δ(2r – x1) в силу условия (3) равна 0. Итак:
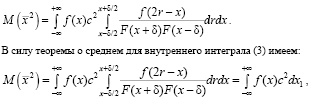
где с(х) некоторая функция от х из интервала [x–δ/2; x+δ/2 ]. Поэтому, пренебрегая бесконечно малыми порядка малости выше δ представим с(х) в виде с(х) = х + о(δ).
В результате получаем:
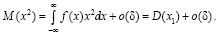(9)
Из равенства (9) и вытекает утверждение о том, что при малых (жестких) допусках качество результатов двух и более измерений превышений на станции совпадает с качеством измерений превышений одним и тем более двумя приемами.
Рассмотрим теперь случай больших допусков, т.е. устремим δ → ∞. Тогда А1 → 1 и fiδ(x) → f(x). Тогда, исходя из (6):
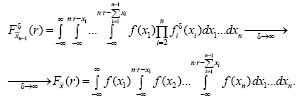
То есть при больших допусках наблюдения можно считать практически независимыми:
.
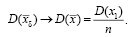Современные цифровые технологии нивелирования II класса, предусматривающие применение высокоточных цифровых нивелиров, укомплектованных кодовыми инварными рейками, позволяют реализовать программу нивелирования на станции, представленную на рисунке 3.
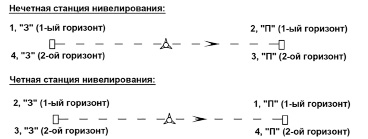
Рис. 3. Реализация цифровым нивелиром программы нивелирования II класса на станции прямого нивелирного хода
Сопоставление программы нивелирования I класса на четной станции правой нивелировки (рис. 2) с программой нивелирования II класса на нечетной станции (рис. 3) указывает на их идентичность друг другу. В целом программа нивелирования I класса на станции отличается от программы нивелирования II класса лишь количеством измеренных превышений (4 и 2 соответственно). Следовательно, при равных внешних условиях нивелирования и допусках на процессы нивелирования, с учетом выражения (9), можно утверждать о равной точности результатов измерения превышений цифровым нивелиром на станции, выполненных по программам I и II классов. Также очевидным является тот факт, что увеличение допуска в n раз снижает точность многократно измеряемой величины превышений примерно в n раз.
Заключение
В результате проведенных теоретических исследований научно обосновано положение о возможности замены нивелирования I класса нивелированием II класса при использовании цифровых нивелиров в комплекте с кодовыми инварными рейками и выполнении определенных условий.
К таким условиям относятся наложение предельно возможных по жесткости допусков в процессе реализации программы нивелирования на нивелирной станции при 2-кратном измерении превышения.
Замена нивелирования I класса нивелированием II класса резко повышает оперативность повторного нивелирования при резком снижении затрат на его исполнение без снижения точности получаемых результатов.