Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Точное и единообразное определение геодезических координат имеет большое практическое значение для широкого спектра задач, связанных с установлением местоположения объектов на Земле [1]. Это, в частности, выполнение измерений на поверхности Земли, установление границ пространственных объектов, оценка смещений природных и техногенных объектов, составление карт и планов, работа навигационных систем, строительство объектов и др. В частности, определение геодезических координат очень важно для единой системы регистрации недвижимости – зданий, сооружений, земельных участков [2, 3]. При проведении строительных, кадастровых работ необходимо точно установить координаты объекта недвижимости в пространстве граничных точек, геометрическую конфигурацию земельных участков, разграничить разные участки. Наличие исчерпывающих, точных, непротиворечивых данных в единых системах, где учитывается недвижимость (например, в России это Единый государственный реестр недвижимости), обеспечивает защиту прав и законных интересов собственников, облегчает сделки, минимизирует конфликты между владельцами земельных участков, упрощает совершение сделок с недвижимым имуществом [4], например земельными участками [5].

С этой целью постановка объектов недвижимости на государственный официальный учет включает обязательное внесение данных о геодезических координатах. Затем они фиксируются в документах по объекту и используются в сделках купли-продажи, аренды, залога и др. [6]. Но в данном случае возникает серьезная прикладная проблема – неточное, с погрешностями определение координат точек на местности. Ошибки определения геодезических координат бывают двух родов [7–9]. Ошибки первого рода – это ошибки средств измерения (геодезических приборов – тахеометров, теодолитов, приемники глобальных навигационных спутниковых систем). Любая измерительная техника имеет определенную погрешность, зависящую от характеристик самого оборудования, условий природной среды, в которой выполняется измерение, методики измерения, квалификации и мотивации геодезиста. Неопытные или недобросовестные специалисты могут применять оборудование с низким классом точности, поэтому могут получить данные с неприемлемым уровнем точности. Тем не менее эти ошибки могут быть минимизированы до необходимого уровня, если квалифицированный мотивированный геодезист использует качественные измерительные приборы. Ошибки первого рода могут считаться субъективными, зависящими от конкретного человека. Их важно верифицировать не зависящими от человека техническими средствами, например, на базе цифровых технологий.

Ошибки второго рода имеют объективный характер. Они вызваны тем, что при определении геодезических координат необходимо перенести данные со сферического объекта (земной поверхности) на плоскость карты, плана. Как известно, ни один из существующих подходов к построению плоскостных карт геоида вращения (отражение сферической планеты Земля на плоской карте) не является идеальным. В любом случае будут происходить искажения и утрата информации. Картографические проекции выбираются в зависимости от того, какая территория должна быть представлена и для какой цели предназначена карта. Наличие разных картографических проекций и систем координат приводит к расхождениям данных. Ошибки второго рода можно назвать ошибками преобразования одной системы координат в другую. В частности, геодезические приборы позволяют использовать для позиционирования объектов в пространстве спутниковые системы навигации (через приемник глобальной навигационной спутниковой сети). В этом случае местоположение объекта определяется по отношению к международным системам координат. Все эти системы являются геоцентрическими. При проведении геодезических работ на местности специалисты определяют координаты объектов по сигналам со спутников. Затем эти данные нужно перенести в другие системы координат.

На локальном уровне для учета объектов недвижимости обычно применяются топоцентрические системы координат. В частности, в субъектах Российской Федерации (регионах России) используются топоцентрические местные системы координат, основанные на эллипсоиде Красовского. Наиболее распространены системы координат 1942 и 1995 гг. (СК-42 и СК-95 соответственно). Например, в Кемеровской области – Кузбассе используется местная система координат МСК-42, основанная на СК-42. Она применяется для проведения кадастровых работ и ведения Единого государственного реестра недвижимости, а также для геодезических работ. Определение координат объектов в системах координат СК-42 и СК-95 на основе метода глобального спутникового позиционирования налагает локальные деформации государственной геодезической сети. Вследствие этого при проведении измерения с помощью метода глобального спутникового позиционирования возникает ошибка локальной деформации государственной геодезической сети в данном месте. Поэтому возникает научная и прикладная проблема нивелирования влияния погрешностей, чтобы получить точные единообразные координаты недвижимости. Эта проблема не имеет однозначного решения в известных исследованиях.

В работе [10] рассматривается преобразование геоцентрических координат в топоцентрические координаты на основе стереографической двойной картографической проекции. Однако размеры объектов (около 10 км2) не соответствуют целям определения координат объектов недвижимости, которые обычно значительно меньше. В [11] анализировалась проблема установления точного и однозначного соответствия измерений в разных системах координат при строительстве солнечных электростанций. Для ее решения рекомендуется установить сеть постоянных контрольных точек с принудительным вводом призм на расстоянии не более 400 м друг от друга, которые визуально доступны в течение всего срока службы станции [12], что неприемлемо для других объектов недвижимости вследствие больших затрат.

В исследовании авторы тестируют гипотезу о возможности использования матрицы деформаций для устранения погрешностей и внесения поправок при точном определении геодезических координат в разных системах. Матрица деформаций является частью метода граничных элементов, эффективного при решении разных задач. Мы полагаем, что если известны параметры взаимного ориентирования двух систем координат, то парные значения можно привести в референцную систему координат и образовать остаточные разности. Это позволит интерполировать разности на регулярную сетку с выбранным шагом и получить матрицу деформаций. Далее эта матрица будет применяться для внесения поправок с помощью специализированного программного обеспечения в автоматическом режиме.

Цель исследования – получение скорректированных координат применительно к системе координат МСК-42 в режиме Real Time Kinematic (RTK) на основе матрицы деформаций для более точного позиционирования геодезического оборудования при установлении координат недвижимости.

Материалы и методы исследования

В работе для получения координат узлов матрицы деформаций использовались метод построения сплайнов минимальной кривизны и метод, базирующийся на триангуляции Делоне с интерполяцией по барицентрическим координатам. Сплайны минимальной кривизны строились с помощью функции «greenspline» в наборе программ с открытым кодом «Generic Mapping Tools» (GMT), распространяемом по лицензии на свободное программное обеспечение «GNU General Public License». Функция используется для работы с декартовыми координатами в одномерном, двумерном и трехмерном пространствах и с координатами на сферической поверхности. Материалами для исследования были 29 географических точек с известными координатами в системах «Государственная система координат 2011 г.» (ГСК-2011) и МСК-42. Координаты были получены от Федерального государственного бюджетного учреждения «Федеральный научно-технический центр геодезии, картографии и инфраструктуры пространственных данных». Они соответствуют пунктам высокочастотной геодезической сети, спутниковой геодезической сети первого класса точности, государственных геодезических сетей первого и второго классов точности.

Результаты исследования и их обсуждение

На первом этапе исследований координаты 29 пунктов были переведены из систем ГСК-2011 и МСК-42 в систему «World Geodetic System 1984» (WGC 84). Координаты из ГСК-2011 переводились в WGS 84 в соответствии с межгосударственным стандартом на методы преобразований координат определяемых точек. Координаты из МСК-42 переводились в WGS 84 с использованием параметров преобразования координат, полученных от Федерального государственного бюджетного учреждения «Федеральный научно-технический центр геодезии, картографии и инфраструктуры пространственных данных». В качестве эталонной разницы в координатах точек принималась разница между значениями ГСК-2011 и WGS 84. Это связано с тем, что методы и алгоритмы соответствующей трансформации установлены межгосударственным стандартом. Разницы между МСК-42 и WGS 84 – это погрешности определения геодезической широты ∆B и геодезической долготы ∆L. В таблице представлены координаты точек x, y, взятые непосредственно из ГСК-2011, а также поправки ∆B и ∆L.

Координаты WGS 84, полученные путем преобразования из системы координат ГСК-2011, и поправки к ним

Соответственно, координаты, взятые из МСК-42, будут иметь вид: широта (y; + ∆B), долгота (x; + ∆L). На следующем этапе исследования было выполнено построение сплайнов минимальной кривизны для получения матрицы деформации в программе «GMT». Построение сплайнов минимальной кривизны основано на функции Грина G (x; s) линейного дифференциального оператора L = L(x). Здесь аргументы x и s могут быть приняты за начальные координаты точек x, y и скорректированные (уточненные) координаты x1, y1. По заданным значениям поправок осуществлялась интерполяция данных. После этого строилась трехмерная модель, где каждой точке поверхности соответствовало значение поправки x + x1 и y + y1. На рис. 1 и 2 показана визуализация поверхностей поправок, полученных с помощью метода построения сплайнов минимальной кривизны. Поверхность поправок для x-координат показана на рис. 1.

Как видно из рис. 1, поправки хорошо визуализируются, что позволяет интерполировать их на референцную сетку координат с известным шагом. На рис. 2 показана аналогичная поверхность поправок для y-координат. Он также демонстрирует четкую визуализацию интересующих авторов объектов. Таким образом, метод построения сплайнов минимальной кривизны в принципе может применяться для уточнения геодезических координат при переходе от одной системы к другой.

Рис. 1. Поверхность поправок ΔL для x-координат, полученных методом построения сплайнов минимальной кривизны

Рис. 2. Поверхность поправок ΔB для y-координат, полученных методом построения сплайнов минимальной кривизны

Также в ходе исследования проводилось построение матрицы деформаций на основе триангуляции Делоне и интерполяции по бароцентрическим координатам. Триангуляция Делоне в двухмерной интерполяции применялась к точкам, полученным преобразованием координат из МСК-42 в WSG 84. Все исходные точки представлены как вершины треугольников (рис. 3).

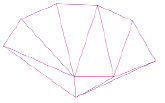
Рис. 3. Представление исходных точек геодезических координат в «WSG 84» как вершин треугольников (после триангуляции Делоне)

Далее для каждого полученного треугольника проводилась интерполяция по барицентрическим координатам, позволяющая рассчитывать поправки в заданной точке матрицы с учетом влияния поправок ΔB и ΔL каждой вершины треугольника, внутрь которого попадает заданная точка. На рис. 4 показан треугольник, где a, b, c являются барицентрическими координатами точки Р. Таким образом, в ходе исследования была показана принципиальная возможность получения матриц деформаций применительно к задаче уточнения геодезических координат двумя методами. Далее это открывает перспективу расчета поправок для x1, y1 по данным о деформациях. Визуализация результатов использования метода показана на рис. 5 и 6, где красным точкам соответствует положение геодезических пунктов. Каждому пикселю на полученной поверхности соответствует значение поправки. На рис. 5 показана поверхность поправок ΔL для координат x.

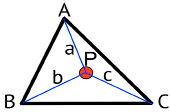
Рис. 4. Точка внутри треугольника, заданная барицентрическими координатами

Рис. 5. Поверхность поправок ΔL для координат x

На рис. 6 показана поверхность поправок ΔB для координат y.

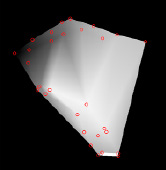
Рис. 6. Поверхность поправок ΔB для координат y

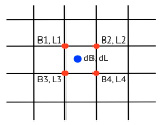
Рис. 7. Исходное положение точки геодезических координат в геоцентрической системе с поправками dB, dL на матрице деформаций

Полученные данные матриц деформации по координатам x и y могут использоваться для расчета поправок при переходе от геоцентрической к топоцентрической системе координат, то есть при переносе данных из результатов съемки на местности в МСК-42. Пример внесения поправок на матрице деформаций показан на рис. 7. Таким образом, в исследовании реализована гипотеза и авторская идея о том, что построение матрицы деформаций (разными методами) позволяет наиболее точно скорректировать полученные при геодезических измерениях координаты.

Кроме того, программная реализация указанных методов в среде «Generic Mapping Tools» позволяет выполнять такие расчеты в автоматическом режиме и исключать субъективные ошибки. Метод матрицы деформаций также открывает возможности для автоматического получения уточненных значений геодезических координат без дополнительных полевых работ. Это снизит расходы, а также исключит влияние низкой мотивации или квалификации специалистов.

Заключение

При проведении геодезических работ возникает необходимость трансформации данных из геоцентрической системы координат (по результатам спутниковой съемки) в топоцентрическую, используемую при ведении государственного кадастрового учета объектов недвижимости. Этот процесс связан с субъективными ошибками, требует больших затрат времени, искажает геодезические данные, необходимые для учета объектов недвижимости. В исследовании поставлена и решена задача автоматизированной корректировки геодезических данных с использованием специализированного программного обеспечения и матрицы деформаций. Показано, что построение матрицы деформаций как методом построения сплайнов минимальной кривизны, так и методом триангуляции Делоне с интерполяцией по барицентрическим координатам дает точные, хорошо визуализированные результаты по поправкам координат x и y. Матрицы деформаций дают возможность рассчитать необходимые поправки в двумерном пространстве ΔB и ΔL. Необходимое значение поправки соответствует пикселям на визуализации деформаций в программной среде «Generic Mapping Tools».

В дальнейшем матрица деформаций может быть использована для внесения поправок с применением специализированного программного обеспечения. В частности, при проведении измерения точки геодезическим оборудованием в режиме RTK сигнал с координатами B, L поступает на сервер с программным обеспечением, на котором по значениям координат определяются ближайшие узлы матрицы деформаций. Путем интерполяции определяются поправки для текущей точки. Поправки вносятся в текущие геодезические координаты, а после сигнал со скорректированными координатами поступает на оборудование. Использование матрицы деформаций также возможно при кабинетных исследованиях при обработке данных. В перспективе использование матрицы деформаций даст возможность получать точные измерения координат на местности непосредственно во время проведения геодезических работ, что снизит расходы денег и времени. Также это исключит объективные и субъективные ошибки специалистов.