Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Трещины массива горных пород представляют собой поверхности разрыва сплошности в горных породах без признака смещения [1]. Они существенно влияют на физико-механические свойства горных пород, и их, в свою очередь, необходимо учитывать при планировании добычных работ и строительстве горнотехнических сооружений [2]. В условиях криолитозоны трещины массива горных пород успешно изучаются с помощью метода георадиолокации [3]. Существуют различные методики выявления трещин массива горных пород по данным георадиолокации [4–6]. Однако применение данных методик ограничивается производительностью операторов-геофизиков, так как данные георадиолокации преимущественно интерпретируются ими вручную. Например, после георадиолокационного исследования на участке АО «Алмазы Анабара» было получено 37 радарограмм по 40000 трасс и 512 точек в каждой, что в общей сумме дает 757 млн значений в матрице.

Для повышения скорости интерпретации данных геофизических измерений возможно использование современных методов анализа цифровых данных, позволяющих не только более качественно обработать геофизические данные по сравнению с традиционными методами, но и провести обработку большого объема данных в короткие сроки. Для изучения трещиноватости мерзлых горных пород по данным георадиолокации возможно применение искусственных нейронных сетей (ИНС) [7], которые позволят проводить анализ георадиолокационных радарограмм с целью выявления разрывов и смещений осей синфазности георадиолокационных сигналов. В последнее время ИНС успешно используются при обработке георадиолокационных данных [8–11].

Целью данного исследования является разработка системы распознавания волновых образов трещин массива горных пород по данным георадиолокационных измерений на основе применения методов искусственного интеллекта.

Существенной проблемой при применении ИНС является подготовка данных для обучения (обучающей выборки). Для подготовки подобных наборов геофизической информации исследователи используют различное программное обеспечение. Например, для генерации синтетических радарограмм в работах [12–14] применялась программа gprMax. Такой подход позволяет автоматизировать формирование обучающей выборки и сгенерировать различные варианты синтетических радарограмм для полноценного обучения нейронной сети. Но, так как принцип работы gprMax основан на решении прямой задачи распространения высокочастотных электромагнитных волн, то данный подход весьма затратный по времени и требует последующей обработки синтетических радарограмм, в частности для разметки в обучающей выборке искомых объектов.

Решение вышеуказанных проблем возможно с помощью модели георадиолокационного разреза массива мерзлых горных пород с трещиной [15]. Разработанное на основе этой модели программное обеспечение в течение 5–10 минут способно сгенерировать до 20 000 обучающих образов с уже нанесенной разметкой для определения положения трещины. Подобная скорость генерации не является избыточной, поскольку параметры обучающих образов напрямую зависят от параметров методики, по которой проведены георадиолокационные измерения. В работе [16] для поиска трещин в асфальтовом покрытии, т.е. при жестко заданных параметрах измерений и исследуемой среды, потребовалось более 5000 обучающих образов. Однако практика использования синтетических радарограмм на основе модели георадиолокационного разреза массива мерзлых горных пород с трещиной показала необходимость ее усовершенствования в плане увеличения количества слоев горных пород, возможности задания наклонных границ с учетом наличия син- и антиформ.

Материал и методы исследования

В модели (1) формируется матрица GPR, в которой каждому столбцу соответствует георадиолокационная трасса с номером Т, а в каждой ячейке (d) столбца хранится амплитудное значение сигнала. Ось синфазности георадиолокационных сигналов представляется в виде Us(T,d) при d, имеющем постоянное значение, для некоторого диапазона значений T (рис. 1). Для описания разрыва оси синфазности использована инвертированная функция прямоугольного импульса 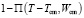, где Tcm – номер трассы, с которой начинается разрыв, Wcm – ширина разрыва, представляющая собой количество трасс, в которых функция Us(T,d) зануляется. Таким образом, приходим к следующему выражению: . Для ввода в модель возможности описания взбросов или сбросов используем функцию Хэвисайда 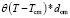, где dcm – количество отсчетов, на которое смещается ось синфазности.

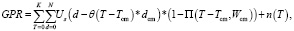(1)

где K – количество трасс, N – количество отсчетов в трассе, Us – форма сигнала, θ – функция Хэвисайда, П – функция прямоугольного импульса, n(T) – помехи.

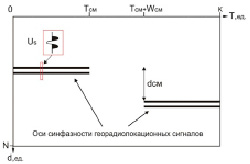
Рис. 1. Схема расположения основных элементов модели радарограммы

Для указания количества границ введем константу M, при этом индивидуальные параметры каждой границы (глубина залегания, изогнутость) задаются соответствующими переменными с индексами s. Для учета наклонных границ при вычислении Us(T,d) введем дополнительное слагаемое kT, увеличивающее время регистрации сигнала при k>0, т.е. граница «уходит» вниз, при k<0, соответственно, вверх. При k=0 граница остается горизонтальной. В данном варианте формулы параметр наклона k будет единым для всех границ. Возможность моделирования осей синфазности георадиолокационных сигналов в виде син- и антиформ представлена в виде слагаемого AI * sin(sai*T). Параметр sai по своей сути задает частоту синусоиды, позволяя моделировать как мелкие колебания, характерные для небольших локальных объектов, так и крупные фрагменты син- и антиформ различной амплитуды AI. При sai = 0 влияние данного слагаемого нивелируется. Модель многослойного георадиолокационного разреза массива мерзлых горных пород с трещиной, учитывающая вышеуказанные особенности, представляется в виде:

(2)

где M – количество границ, GGS – положение по глубине s-й границы, k – параметр наклона оси синфазности сигналов, AI – амплитуда изгиба границы, sai – параметр изогнутости.

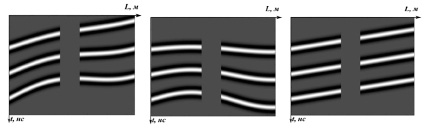
Апробация численных расчетов модели по формуле (2) была реализована в Matlab для четырехслойного разреза. В качестве формы сигнала Us использована вторая производная функции Гаусса, для границ варьировались следующие значения параметров: k, AI, sai. Результаты моделирования представлены на рисунке 2.

На основе сгенерированных синтетических радарограмм была сформирована обучающая выборка для модели ИНС. Выборка состояла из 50000 пар синтетических радарограмм, представляющих собой изображения размером 32×32 пикселя с нанесенной разметкой положения трещины в виде зеленых пикселей (рис. 3б) и без нанесенной разметки (рис. 3а). Радарограммы без разметки используются в качестве входных данных, радарограммы с разметкой применяются в качестве целевых данных для вычисления функции потерь модели. После генерации контрастность синтетических радарограмм повышается до максимума для выделения границ слоев.

а) б) в)

Рис. 2. Результаты моделирования по формуле (2) с параметрами: а) k = 0,3; AI = 0,1; sai = 0,015; б) k = 0; AI = 0,1; sai = 0,015; в) k = 0,3; AI = 0; sai = 0

Архитектуры нейронной сети

а) б)

Рис. 3. Пример результата моделирования радарограммы: а) без нанесенной разметки положения трещины; б) с нанесенной разметкой положения трещины

В настоящее время разработано множество различных типов ИНС. В предыдущем исследовании [17] была выбрана ИНС типа сверточный автоэнкодер. Сверточный автоэнкодер – это тип ИНС, который использует сверточные слои вместо полносвязных. Он состоит из двух основных частей: энкодера и декодера. Энкодер принимает входные данные и пропускает их через сверточные слои, сокращая размерность данных. Результат этого процесса – «латентное», или «скрытое», представление входных данных, которое охватывает наиболее важные аспекты входных данных. Декодер затем принимает этот латентный код и преобразует его обратно в оригинальное пространство входных данных [18].

В нашем исследовании энкодер и декодер состоят из трех сегментов, каждый из которых оснащен сверточным слоем с параметрами ядра 3×3 и шагом 1, слоем активации ReLU, а также слоем MaxPooling, сокращающим размерность, или UpSampling, повышающим размерность. Данная архитектура была выбрана эмпирически из множества архитектур и достигает 98% точности по метрике – косинусное сходство. Остальные варианты с большим или меньшим количеством сегментов или нейронов не смогли достичь той же точности по причине переобучения либо, наоборот, по причине недообученности. Таким образом, была выбрана архитектура ИНС под 5 номером, так как она обладает наиболее подходящим количеством сегментов и нейронов (таблица).

Принцип работы выбранной архитектуры заключается в том, что энкодер сжимает входное изображение до размеров 8×8 пикселей, после чего декодер преобразует его обратно к исходной размерности 32×32 пикселя, уже с выделенными положениями трещин.

Обучение модели производилось с использованием оптимизатора Adam с коэффициентом скорости обучения 0.001 и функции потерь в виде бинарной кросс-энтропии. Для регулирования сети применялся dropout 0.2 после каждого сверточного слоя. Сгенерированный набор данных был разбит на 3 подгруппы: 40000 экземпляров были выделены для обучения модели, 9000 экземпляров – для вычисления ошибки и 1000 экземпляров – для валидации. Примеры результатов, полученных с помощью обученной модели автоэнкодера, представлены на рисунке 4.

а) б)

Рис. 4. Пример результата работы модели ИНС: а) фрагмент радарограммы до обработки; б) фрагмент радарограммы после обработки

Результаты исследования и их обсуждение

Апробация работы модели ИНС проведена на данных георадиолокационного исследования массива мерзлых горных пород криолитозоны. Результат обработки представлен на рисунке 5, на котором в интервале от 80 до 300 наносекунд можно наблюдать значительное количество смещений и разрывов осей синфазности георадиолокационных сигналов. В промежутках от 0 до 80 наносекунд и от 300 до 325 наносекунд находятся непрерывные оси синфазности. Стоит отметить, что именно в областях с большим числом смещений и разрывов осей синфазности модель нейронной сети идентифицировала положения трещин, в то время как на участках с непрерывными осями синфазности положения трещин не были обнаружены. В области, выделенной пунктирной линией, заметны малоамплитудные сигналы, которые соизмеримы с уровнем шума. Это усложняет процесс распознавания положений трещин.

Следует отметить, что «горбы», возникающие на осях синфазности из-за дискретизации сигнала и прерывания тонкой линии (от 0 до 15 м на 240 нс), модель ИНС не определяет как трещины. Это стало возможным благодаря операциям уменьшения размерности, которые обнуляют данные явления, что подтверждает правильный выбор архитектуры нейронной сети.

Тем не менее, в работе модели наблюдаются некоторые недостатки. В частности, модель ИНС ошибочно выделяет пустоты в осях синфазности как трещины, расположенные на 140-м метре и 80 нс или на 130-м метре и 200 нс. Причина этого заключается в том, что модель ИНС принимает пустоты за разрывы осей синфазности. Еще одна ошибка находится на 30-м метре и 210 нс, где модель ИНС идентифицировала деформацию оси синфазности, образованную вследствие помех, как трещину. Кроме того, модель ИНС не всегда способна различить конец оси синфазности и трещину, что наблюдается на 70-м метре и 190 нс или 100-м метре и 350 нс. Решение этой проблемы может заключаться в расширении обучающего набора соответствующими данными. Однако такие случаи встречаются довольно редко и не оказывают существенного влияния на результат интерпретации данных.

Также следует упомянуть, что для удобства интерпретации трещины, представляющие собой отдельную систему, необходимо выделять как некоторую ограниченную область, например в интервале от 135 до 150 м и от 70 до 120 нс. Для решения данной проблемы можно использовать дополнительную модель ИНС, находящую области трещиноватости на основе уже найденных трещин.

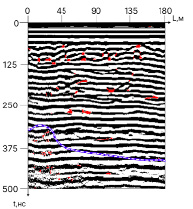
Рис. 5. Пример результата работы модели ИНС

Заключение

Разработана система распознавания волновых образов трещин массива горных пород по данным георадиолокационных измерений на основе применения методов искусственного интеллекта. Для создания обучающего набора данных использовалась модель георадиолокационного разреза массива мерзлых горных пород с трещиной [15], которая была усовершенствована для задания нескольких границ слоев и наклонных границ. На основе разработанной модели был создан обучающий набор, состоящий из 100000 синтетических радарограмм. Выбранный сверточный автоэнкодер был оптимизирован по количеству слоев и нейронов. После обучения была проведена апробация разработанной модели ИНС на данных георадиолокационного исследования массива мерзлых горных пород криолитозоны. Апробация модели ИНС показала высокую эффективность модели ИНС. Тем не менее, в работе модели наблюдаются некоторые недостатки.

Разработанная система позволит существенно сократить временные затраты на интерпретацию данных георадиолокации. Дальнейшие исследования будут связаны с повышением точности предсказания, обусловленным расширением обучающего набора данных и разработкой дополнительной модели ИНС.