При разработке месторождений криолитозоны необходима информация о криогенном состоянии горных пород. Подобную информацию возможно получить по данным бурения скважин и проходки шурфов, но наиболее информативными методами являются геофизические. Из них при изучении строения массива горных пород россыпных месторождений криолитозоны успешно применяется метод георадиолокации [1]. Информацию о криогенном состоянии горных пород методом георадиолокации [2; 3] получают с помощью использования специализированных методик: 1) разнос антенн; 2) анализ гиперболических осей синфазности георадиолокационных сигналов.
Первый способ заключается в последовательном увеличении расстояния между передающей и приемной антеннами (от десятков сантиметров для высокочастотных георадаров до нескольких метров для низкочастотных) по поверхности Земли. Цель таких наблюдений состоит в получении графика зависимости времени прихода отраженных волн от расстояния и определении, с помощью последующей обработки, сведений о скоростях распространения электромагнитных волн в среде. Однако из-за огромных затрат времени на производство работ данная методика применяется весьма редко [4, c. 43].
Второй способ основан на явлении дифракции электромагнитных волн (ЭМВ). На радарограмме электромагнитные волны, отраженные от локального объекта, образуют гиперболические оси синфазности георадиолокационных сигналов. Анализ формы такой гиперболы позволяет определить глубину залегания локального объекта и скорость распространения электромагнитных волн в среде выше него. Далее, основываясь на отношении зависимости скорости и относительной диэлектрической проницаемости (ε) среды, можно сделать вывод о криогенном состоянии и строении подповерхностных слоев [5, с. 12].
Одной из проблем при изучении криогенного строения массива горных пород является определение местоположений подповерхностных подземных льдов, что важно при проведении буровзрывных работ на месторождениях криолитозоны. Для решения данной проблемы была поставлена следующая цель: разработать алгоритм обработки данных георадиолокации, позволяющий выявлять подповерхностные подземные льды в массиве мерзлых горных пород.
Для достижения этой цели необходимо решить следующие задачи:
1) провести анализ криогенного строения массива горных пород россыпных месторождений криолитозоны;
2) определить условия, при которых данные об электрофизических свойствах горных пород, полученные на основе анализа гиперболических осей синфазности георадиолокационных сигналов, будут наиболее информативны;
3) разработать алгоритм и реализующее его программное обеспечение, позволяющие выявлять подповерхностные подземные льды в массиве горных пород криолитозоны.
Материалы и методы исследования
Большинство россыпных месторождений криолитозоны относятся к аллювиальному типу. Развиты повсеместно четвертичные образования, представленные широким набором генетических типов отложений: аллювиальными, озерно-аллювиальными, озерно-болотными, полигенными и т.д. Рыхлые отложения в большинстве представлены льдистыми алевритами, суглинками, илами, илистыми песками, глинами, реже супесями, песками и торфом с линзами и жилами льда [6, с. 71]. Например, на россыпном месторождении алмазов льдистость массива горных пород составляет до 60 %. Мощность ледяных жил, как правило, контролируется мощностью рыхлых отложений и не превышает 2–4 м, возрастая в пределах аллювиальных террас, полигональных и плоскобугристых торфяников до 5–7 м [7, с. 246]. Таким образом, в типичном геокриологическом разрезе массива горных пород присутствуют приповерхностные льды, ниже которых расположены нарушенные коренные породы, формирующие гиперболические оси синфазности георадиолокационных сигналов.
Для обработки и интерпретации данных георадиолокационных измерений, как правило, используются программные комплексы, идущие в комплекте с георадарами, например GeoScan32 (НПЦ ГЕОТЕХ). В данном программном комплексе выделение дифрагированных осей синфазности сигналов осуществляется оператором-геофизиком вручную путем подбора годографа подходящей формы. Для автоматизации процесса уточнения формы гиперболического годографа необходимо создать соответствующий алгоритм. В настоящее время в данной области имеются разработки, представленные исследованиями российских и зарубежных авторов. Среди них есть много работ, связанных с созданием алгоритмов на основе преобразования Хафа, как, например, в работах [8; 9].
Преобразование Хафа (Hough Transform) – это пространственный фильтр обнаружения графического примитива на изображениях с использованием процедуры «голосования». В данном исследовании для автоматизации изучения гиперболической формы осей синфазности сигналов был создан алгоритм, использующий методы на основе преобразования Хафа.
Описание работы алгоритма
Графическое изображение радарограммы обрабатывается ранее созданной программой для детектирования гиперболических образов [10]. Ограничение каждого региона представлено двумя координатами: первая локализует правый верхний угол, вторая – левый нижний. Локализация таких регионов проводится с использованием методов машинного обучения. Программа, созданная в рамках данного исследования, принимает на вход указанные выше регионы – прямоугольные области изображения радарограммы R_, содержащие изображения гиперболических осей синфазности сигналов.
В данной работе описан алгоритм реализации следующего логического этапа – уточнение формы гиперболических кривых, образованных осями синфазности и локализация пространственно-временного расположения их вершин.
Начальная матрица R_ {i, j} пиксельного пространства была приведена в соответствие пространству R {x, t}, где x – протяженность профиля исследований, t – время распространения сигнала в среде.
Фазовое пространство Хафа – Hough Space (HS) представляет собой двумерную плоскость, образованную координатными осями Oυ и Oh. По оси Oυ отмечаются скорости прохождения ЭМВ в среде, а по оси Oh – координаты вершины гиперболической кривой по оси времени, пересчитанные в глубинные значения с помощью уравнения
h = (t × υ) / 2, (1)
где t – двойное время пробега электромагнитной волны. Таким образом, каждому из k возможных положений вершины Ok (x, t) исходного пространства R соответствует прямая в HS с угловым коэффициентом t/2.
Каждая точка (υp, hk) прямой аккумулирует значения амплитуд:
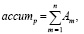 (2)
(2)
где Am – амплитуды сигналов, хранящиеся в точках (xm, tm), проходящих вдоль гиперболического годографа пространства R (3).
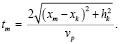 (3)
(3)
В аккумуляторе HS для каждой из k вершин сохраняется максимальное накопленное значение: accumk = Max(accump). Затем из массива вершин Ok выбирается та, которой соответствует максимальный накопитель.
Таким образом, процедура «голосования» проходит дважды: итогом первого является определение значения скорости υ для каждой из возможных k вершин, по итогу второго голосования выбирается вершина оси синфазности.
Каждое вычисляемое значение t уравнения годографа (3) для фиксируемых υ и x отображается на исходное пространство с приблизительной точностью, поэтому значение амплитуды в этой точке определяется по двум соседним точкам, проходящим по годографу дифракции (рис. 1).
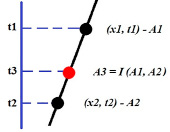
Рис. 1. Значение амплитуды по ближайшим точкам
Если t3 – вычисленная вторая координата точки исходного пространства для заданной x3, а (x1, t1, A1) и (x2, t2, A2) – ближайшие соседние координаты точки, пробегающие по годографу дифракции и хранящие амплитуды сигналов, то амплитуда для точки (x3, t3) будет вычисляться по формуле
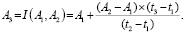 (4)
(4)
Итогом работы алгоритма является определение местоположения вершины оси синфазности в пространстве {x, t}, и скорость (υ) распространения ЭМВ в среде выше локального объекта. Полученное значение скорости используется для определения относительной диэлектрической проницаемости среды:
ε = c2 / υ2. (5)
Оптимизация алгоритма
Использование алгоритма Хафа на практике имеет один существенный недостаток: высокая асимптотическая сложность O(nk), где n – размер исследуемой области, k – размерность фазового пространства. Для снижения сложности алгоритма, как правило, ищут способы уменьшения числа итераций при вычислении аккумуляторов. Например, в своем исследовании китайские авторы Цзянь Ван и Йи Су уменьшили количество исходных параметров фазового пространства с трех- до одномерного [8]. В результате работы с помощью созданного алгоритма им удалось снизить вычислительную нагрузку до O(M×N), но, как отмечают сами авторы, в практических приложениях способность к обнаружению осей синфазности сигналов была невысокой.
Некоторые исследователи, как, например, в работе по обнаружению осей синфазности георадиолокационных сигналов без априорных знаний о среде [9], предлагают методы анализа дифрагированных осей синфазности с помощью свертки образа на изображении радарограммы, с гиперболой, заданной уравнением годографа. Предложенная этими авторами методика похожа на представленную в данной работе, но далее они пытаются сопоставить уравнение годографа с каноническим уравнением гиперболы. Особенность указанного алгоритма состоит в том, что метод учитывает деформацию картины волнового образа осей синфазности. В результате, алгоритм успешно справляется с локализацией гиперболических образов, представленных осями синфазности, но авторы работы указывают на довольно высокую ошибку при оценке относительной диэлектрической проницаемости среды.
Для уменьшения программной сложности в данном исследовании также были предприняты следующие шаги:
Шаг 1. Заполнение аккумулятора в HS является основной частью созданного алгоритма, производительность которого зависит, во-первых, от размерности задания пространства, во-вторых, от количества параметров перебираемых значений и, в-третьих, от величины шага перебираемых значений последовательности исходного и накопительного пространств.
В реализованном подходе точность определения местоположения координат вершины оси синфазности (ВОС) пространства R зависит от учета всех точек, проходящих вдоль ее годографа. Поэтому увеличение шага дискретизации в исходном пространстве было бы некорректным.
Шаг 2. Была ограничена область локализации ВОС. В созданном алгоритме была уменьшена область определения координат вершин: по оси Ot наполовину и по Ox – втрое:
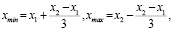
 (6)
(6)
где (x, t) – координаты ВОС. Сокращение количества вершин-кандидатов в исследуемом регионе пространства R привело к уменьшению числа итераций циклов и в конечном итоге повысило производительность алгоритма. Следует подчеркнуть, что данное ограничение не является обязательным, поскольку поиск вершины уже проводится в пределах пространства R.
Шаг 3. Важное ограничение было введено в фазовом пространстве: перебор значений скорости проводится в пределах области допустимых значений:
υmin = 0.1 м/нс, υmax = 0.167 м/нс, (7)
Результаты исследования и их обсуждение
Апробация алгоритма проведена на данных компьютерного моделирования распространения ЭМВ (синтетической радарограмме), полученной в системе gprMax на основе схемы, представленной на рис. 2, а. Значениям ε на радарограмме соответствовали: мерзлые горные породы (ε1 = 4), лед (ε1 = 3,2), воздух (ε1 = 1). Третий вариант расположения локального объекта под слоем воздуха предназначен для определения на радарограмме возможных помех от деревьев, строений, техники и пр. Соответственно, область допустимых значений скорости ЭМВ была изменена: максимальная скорость была увеличена до 0,33 м/нс. Результат работы алгоритма отображен на рис. 2, в.
В результате апробации алгоритма на синтетических данных для каждой из модельных сред были получены следующие значения (соответственно):
υ1 = 0,146 м/нс, t1 = 15,18, ε1 = 3,95,
υ2 = 0,162 м/нс, t2 = 15,24, ε2 = 3,204,
υ3 = 0,277 м/нс, t3 = 15,18, ε3 = 1,095.
Разница в значении ε составила 0,055; 0,004 и -0,095 соответственно. Таким образом, отклонение от модельных данных составило около 1,4 %, что с учетом погрешностей измерений на синтетической радарограмме показывает удовлетворительный результат.
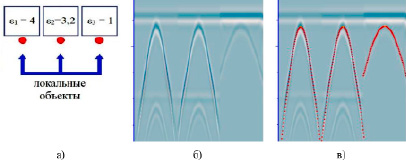
Рис. 2. Апробация программного алгоритма: а) описание заданных электрофизических свойств среды; б) синтетическая георадиолокационная радарограмма; в) выделенные оси синфазности
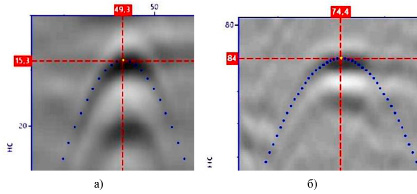
Рис. 3. Результаты тестирования на полевых данных: а) υ = 0,16 м/нс, t = 15,23 нс, ε = 3,13; б) υ = 0,15 м/нс, t = 84,38 нс, ε = 3,5
Проверка работы алгоритма была также проведена на полевых данных (рис. 3) георадиолокационных исследований массива мерзлых горных пород. В результате была определена пространственно-временная локализация объектов и значение относительной диэлектрической проницаемости среды. Полученные значения соответствовали ожидаемым.
Заключение
В результате проведенных исследований создан алгоритм на основе преобразования Хафа для определения электрофизических свойств подповерхностной среды по локализованным осям синфазности сигналов георадиолокации. Тестирование, проведенное на синтетической радарограмме, показало точность определения алгоритмом значений относительной диэлектрической проницаемости 98,6 %. Разработанный алгоритм позволит увеличить скорость обработки и интерпретации георадиолокационных исследований и может быть использован для картирования подповерхностных подземных льдов в массиве горных пород криолитозоны.
Основная работа по оптимизации производительности алгоритма в данное время проводится в фазовом пространстве. Было замечено, что локальные максимумы накопителей каждой прямой, соответствующей вершине гиперболического годографа в исходном пространстве, аппроксимируют в фазовом пространстве некоторую кривую. Таким образом, в первом голосовании достаточно определить начальный и конечный максимумы в накопительном пространстве, затем, построив график искомой функции, сразу перейти ко второму голосованию – поиску максимума аккумулятора в точках на этом графике. В следующей работе будет проведено исследование данной кривой.



