На перспективных площадках строительства прецизионных сооружений, примерами которых являются объекты атомной энергетики, инженерно-строительные комплексы линейных ускорителей заряженных частиц, промышленные конвейеры тонких технологий и других объектов, надежность сооружений в процессе эксплуатации обеспечивается прежде всего допустимыми деформациями оснований их фундаментов, определяемыми большей частью десятыми долями миллиметров (0,1–0,5 мм) [1, с. 381; 2; 3].
Опыт эксплуатации прецизионных сооружений показывает [2–4] на наличие нарушений устойчивости прецизионных сооружений, обусловленных воздействиями природных и техногенных геомеханических процессов на основания их фундаментов. При этом неоднородные инженерно-геологические условия застраиваемой промплощадки порождают сложнодифференцированные деформации оснований сооружений экзогенного происхождения, которые со временем не прекращаются и могут являться причиной нарушения устойчивости прецизионных сооружений [2].
В этой связи на стадии выбора площадки под строительство прецизионных сооружений в составе инженерных изысканий производится изучение микросмещений приповерхностных слоев земной коры на глубине закладки фундаментов, вызванных как короткопериодическими, так и длительными воздействиями экзогенных геомеханических процессов [4]. В силу инженерно-геологической неоднородности приповерхностных слоев земной коры по глубине и простиранию, экзогенные геомеханические процессы оказывают различные возмущающие воздействия на различные породы четвертичных отложений, порождая при этом неоднородное напряженно-деформированное состояние приповерхностных слоев земной коры. Это обстоятельство, одновременно с процессами современной геодинамики, неизбежно приводит к дифференцированным вертикальным смещениям приповерхностных слоев земной коры и нивелирных пунктов [2; 5–7], закладываемых на специальных геодезических площадках (рисунок), предназначенных для изучения этих вертикальных смещений.
Материалы и методы исследования
Традиционно [1, с.160; 3] смещения нивелирных пунктов определяют по результатам повторного нивелирования нивелирных пунктиков на основе изменения превышений между исходным и контрольными пунктами. При этом в качестве начала координат (высот) применяются дорогостоящие, сложные по конструкции глубинные нивелирные пункты (реперы) [3; 4], не обладающие абсолютной устойчивостью [2].
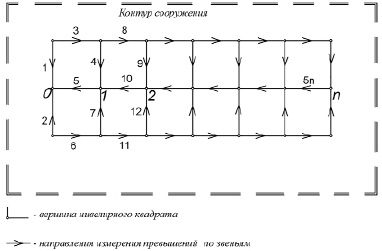
Схема специальной наблюдательной геодезической сети из сдвоенных нивелирных квадратов
В отсутствие на Земле абсолютно неподвижных точек, авторами статьи разработан альтернативный метод математической обработки результатов повторного нивелирования без выбора исходного (опорного) нивелирного пункта.
Прелагаемый метод предусматривает проверку равноточности результатов наблюдений или их распределения и интервальную оценку разностей превышений ∆hi, полученных в i-х циклах наблюдений и установления значимости изменения превышений [3]:
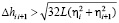
или vзн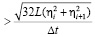 
, (1)
где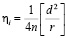 
– случайная среднеквадратическая ошибка измерения превышений в i-м цикле повторного нивелирования [8, с. 5], d = hcp – hобр – разность превышений, полученных в N секциях прямых и обратных ходов, длина которых L км; vзн – значимая величина скорости изменения превышений ∆hi i+1.
Поочередно принимая за исходный все нивелирные пункты по уравненным превышениям, вычисляются высоты остальных j-х. Основываясь на сопоставлении отметок всех нивелирных пунктов из двух циклов повторных наблюдений, получаем n рядов расхождений высот ∆ij (i, j от 1 до n). Полученные расхождения сводятся в квадратическую симметричную матрицу:
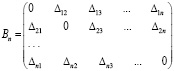. (2)
Разделив суммы столбцов Si матрицы Bn на n (количество пунктов), получаем средние смещения j-х пунктов Δср(j) относительно всех остальных нивелирных пунктов. По значениям средних смещений Δср(j) и промежутку времени Δt между повторными нивелированиями на участке L между нивелирными пунктами j и j+1 получим средние скорости vср вертикальных движений и их градиенты, а именно:
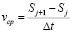
и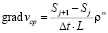 
, (3)
где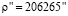 
.
Полученные значения скоростей вертикальных смещений нивелирных пунктов v при выполнении условия (1) невозможно объяснить систематическими ошибками нивелирования так как их влияние на точность измерения превышений в ходах нивелирования длиной менее 20 км, что характерно для специальных геодезических сетей, пренебрежимо малое и составляет сотые доли миллиметров [1; 8, с. 5]. Значение среднеквадратических ошибок, установленных средних смещений Sj нивелирных пунктов характеризуется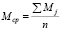 
.
Погрешность определения средней скорости смещения оснований прецизионных сооружений на участке между i-м и j-м нивелирными пунктами определяется формулой
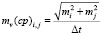, (4)
где ∆t – промежуток времени между сопоставляемыми повторными нивелированиями нивелирных пунктов, заложенных на глубину оснований прецизионных сооружений.
Для вычисления среднеквадратических погрешностей mv(cp)i,j составляется матрица An среднеквадратических погрешностей повторного нивелирования соответственно матрице Bn:
.
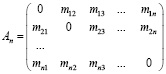Разработанный метод одновременно с вычислением вертикальных смещений, скоростей современных движений приповерхностных слоев земной коры и их градиентов позволяет оценить устойчивость нивелирных пунктов, заложенных на глубину оснований прецизионных сооружений, а также выбрать исходный пункт (начало высот) для определения крена приповерхностного слоя земной коры, составляющего основание сооружения. Градиент скорости, свободный от накопления значительной части ошибок повторного нивелирования [2], характеризует развивающийся крен приповерхностного слоя земной коры, который является предметом исследования на перспективных площадках строительства прецизионных сооружений.
Для уравнивания измеренных превышений в часто встречающейся в практике нивелирной сети [1; 2], состоящей из сдвоенных нивелирных рядов из одинаковых квадратов (рисунок), разработан строгий способ уравнивания, который по сравнению с известными в геодезической практике способами более компактный, упрощающий уравнительные вычисления и оценку точности.
Разработанный строгий способ уравнивания предусматривает решение системы нормальных уравнений коррелят с пятидиагональной матрицей коэффициентов. Для сдвоенных нивелирных рядов из одинаковых квадратов (рисунок) коэффициенты нормальных уравнений коррелят представляют пятидиагональную матрицу и определяются равенством
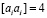при i от 1 до 2n и
при i от 1 до 2n-1.
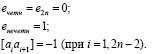(5)
Обозначив коэффициенты условных уравнений буквами a1, a2, a3 и т.д., представим преобразованную (по Гауссу) систему нормальных уравнений коррелят в следующем виде:
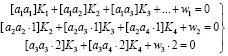. (6)
Рассмотрим систему (6) в виде одного общего равенства:
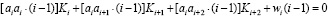. (7)
Преобразованные квадратические коэффициенты можно представить в виде простых дробей [2], а именно:
. (8)
Очевидно, что квадратические коэффициенты, полученные от сочетания несмежных квадратов с разностью индексов n > 2, равны нулю:
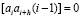, при n ≥ 3, (9)
а неквадратические коэффициенты от сочетания смежных квадратов равны
; (10)
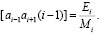(11)
Алгоритм Гаусса преобразования свободного члена в раскрытом виде состоит из трех членов:
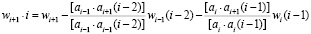. (12)
Для получения формулы преобразованного свободного члена, преобразуем алгоритмы Гаусса через целые числа М и Е:
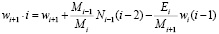. (13)
Назначим обозначения:
, 
, 
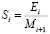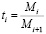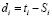. (14)
С учетом принятых обозначений (14) представим рабочую формулу для вычисления последовательных значений преобразованных свободных членов нормальных уравнений коррелят, а именно:
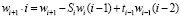. (15)
Результаты исследования и их обсуждение
С практической целью целесообразно упростить обозначения алгоритма Гаусса для преобразования члена, не теряя при этом никакой информации, содержащейся в этом алгоритме, представим преобразованный свободный член как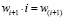 
.
Тогда формула (15) для вычисления преобразованного свободного члена будет представляться в следующем виде:
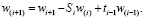(16)
Контрольные вычисления преобразованных свободных членов можно производить по формуле контрольной суммы, имеющей следующий вид:
.
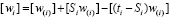При вычислении величины ti и Si используются числа М и Е, которые вычисляются по рекуррентным формулам, представленным, как и алгоритм вычислений, в опубликованной ранее работе [2], а именно:
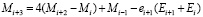
и 
. (17)
Равенство (17) с учетом условий (5) и значений 
(при n = 1, …, i) является возвратным уравнением для чисел М, позволяющих получить квадратичные члены по формуле (8).
Формулы для вычисления коррелят получаем подстановкой в уравнение (7) значения коэффициентов при коррелятах, полученных согласно (8)–(11), что позволяет с учетом (13) и (14) получить выражения текущей корреляты через предыдущие и преобразованные свободные члены:
.
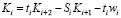Контроль вычисления коррелят производится по общеизвестной формуле суммы всех нормальных уравнений
,
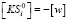где 
– сумма коэффициентов i-го нормального уравнения коррелят.
Заключение
Решение системы нормальных уравнений коррелят с пятидиагональной матрицей коэффициентов при математической обработке результатов наблюдений за экзогенными и эндогенными геомеханическими процессами, полученных на основе повторного высокоточного нивелирования сети, представленной 12 сдвоенными квадратами, показало хорошие результаты. Так, контроль выполненных преобразований свободных членов показал, что вычисления выполнены с точностью 0,01 мм, а суммы произведений коэффициентов на соответствующие корреляты без свободного члена близки к нулю (-0,03; -0,05 мм), то есть контроль выполняется.
Применение разработанного метода постановки и методики обработки результатов повторных геодезических наблюдений позволяет повысить репрезентативность результатов экспериментальных исследований современных геодинамических исследований [9] с использованием данных деформационного мониторинга природных и техногенных систем.