Экологическая ситуация природных вод как в России, так и в мире в целом, порождена системой нерационального, расточительного природопользования [1]. Предприятия ежедневно выбрасывают в атмосферу тонны пыли и частицы вредных веществ. Продукты переработки сливаются в реки и моря, не подвергая очистке или недостаточно очищая. Таким образом, появляется проблема чистой воды [2].
Сточные и промывные воды производства имеют в своем составе ионы тяжелых металлов – кадмия, никеля, меди, цинка, марганца и др. Соединения ионов тяжелых металлов обладают специфическими токсичными свойствами, что наносит вред на экосистему окружающего мира. Самым эффективным способом очистки воды от тяжелых металлов является адсорбционная технология [3, 4].
Широкое применение в качестве сорбентов нашли природные глинистые минералы. Глинистый минерал содержащий монтмориллонит представляет алюмосиликатный минерал группы смектитов подкласса слоистых силикатов. Структура монтмориллонита отличается симметричным сложением пачек слоев. Расстояние между пакетами изменяется от 0,4 до 2,0 нм. В результате изоморфных замещений в решетке ионов Al3+ на Fe2+ или Si4+ на Al3+ при этом возникает избыток отрицательного заряда, который компенсируется ионами Na+, K+, Ca2+, Mg2+. Строение кристаллической решетки монтмориллонита определяет высокую ее активность и емкость.
В настоящей работе устанавливаются характеристики сорбции ионов кадмия на монтмориллонитовой глине, необходимых для проектирования установок по очистке воды.
Материалы и методы исследования
В работе использована природная глина, содержащая монтмориллонит. Химический состав определялся растровой электронной микроскопией с использованием электронного микроскопа JEOLJSM 6510 LV. Состав оксидов в монтмориллонитовой глины: SiO2 – 54,0%; Al2O3 – 20,73%; Na2O – 0,75% ; K2O – 3,07% ; CaO – 0,44%; Fe2O3 – 9,43%; TiO2 – 1,1%; MgO – 1,82%. При прокаливании потери составляют 8,66%. В составе оксидов присутствуют Na2O и K2O и представляют водорастворимые оксиды в объеме 3,82%, которые способны замещаться на другие ионы.
На рис. 1 представлен фазовый состав природной монтмориллонитовой глины. Рентгенофазовым анализом на дифрактометре «ДРОН-7» с медным анодом (λ=1,5406 Å) был установлен минералогический состав.
Из полученных данных видно, что основной состав представлен монтмориллонитом (47%) и сопутствующими глинистыми минералами (гидрослюдами, хлоридом и каолинитом). Общий состав глинистых минералов – 89%.
Изучение адсорбции ионов кадмия проходилось в статических условиях. Монтмориллонитовая глина предварительно рассеивалась по фракциям. Образцы брались с размерами из фракции 0,25 – 0,5 мм. Влияние концентрации ионов кадмия на адсорбцию осуществлялось на 1 г сорбента в контакте с 50 мл раствора. Остаточное содержание Cd2+ определяли по методике [5].
Используя средние значения равновесных концентраций (использовали два параллельных измерения) определили величину адсорбции:
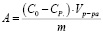 (1)
(1)
где А – обменная емкость ионов, ммоль/г; C0 – начальная и CP. – равновесная концентрации ионов Cd2+, ммоль/мл; Vp-pa – объем исследуемого раствора, мл.
Результаты исследования и их обсуждение
Адсорбционные свойства монтмориллонитовой глины определяли с помощью изотерм (рис. 2). Полученные экспериментальные данные показывают, что с увеличением концентрации ионов в растворе возрастаетадсорбция ионов кадмия. Изотермы имеют вид резкого подъема начального участка изотерм. Затем идет насыщение поверхности сорбента.
Оценку сорбции ионов кадмия производили с использованием моделей Ленгмюра, Фрейндлиха и Темкина.
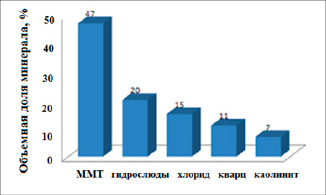
Рис. 1. Фазовый состав монтмориллонитовой глины (ММТ – монтмориллонит)
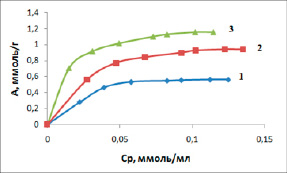
Рис. 2. Изотермы сорбции ионов кадмия на монтмориллонитовой глине, К: 298, 318, 333
Таблица 1
Адсорбционные характеристики поглощения ионов кадмия по моделям
|
Т, К |
Ленгмюра |
Фрейндлиха |
Темкина |
||||||
|
A∞, ммоль/г |
kL, мл/ммоль |
R2 |
kF |
n |
R2 |
lgkT |
α |
R2 |
|
|
298 |
0,62 |
95,41 |
0,999 |
5,19 |
14,02 |
0,973 |
21,79 |
29,41 |
0,859 |
|
318 |
1,04 |
87,09 |
0,999 |
9,42 |
6,09 |
0,971 |
20,66 |
16,39 |
0,976 |
|
333 |
1,29 |
77,30 |
0,999 |
20,42 |
5,38 |
0,976 |
18,95 |
11,90 |
0,981 |
Модель Ленгмюра построена на основе молекулярно-кинетической теории и мономолекулярном процессе адсорбции. Уравнение линейной изотермы имеет вид:
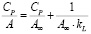 (2)
(2)
Используя модель Ленгмюра (рис. 3) определили постоянные параметры: предельную величину адсорбции A∞ и константу адсорбционного равновесия kL.
Модель Фрейндлиха в логарифмической форме
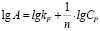 (3)
(3)
дает возможность построить линейную зависимость в координатах lgA – lgC и определить постоянные константы kF и n.
Модель Темкина в линейной форме:
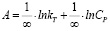 (4)
(4)
Содержит параметр, который учитывает взаимодействие между адсорбционными центрами и адсорбированными ионами.
В табл. 1 приведены данные полученные при обработке изотерм.
Исследования адсорбционных свойств природных глин показали, что в её состав входит не один минерал, а ему сопутствуют в разных количествах другие минералы. Это отражается на пространственной структуре с изменением геометрии частиц. Поэтому при расчетах сорбционных характеристик получили разные значения коэффициентов корреляции по моделям. Модель Ленгмюра уточняет, локализацию адсорбции на отдельных адсорбционных центрах и образует монослой [5]. При этом адсорбированные молекулы не взаимодействуют друг с другом. Кроме этого все адсорбционные центры энергетически эквивалентны. В реальности при использовании природных минералов допускается погрешность.
Модель изотермы Фрейндлиха используют при обработке данных с неоднородной поверхностью сорбента. Природные минералы глин представляют неоднородную поверхность. Процесс адсорбции это экзотермический процесс, протекающий с выделением тепла. Это можно объяснить тем, что происходит отталкивание сорбат – сорбат и адсорбция проходит с равным распределением энергии связывания.
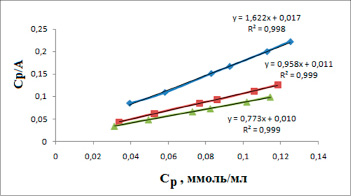
Рис. 3. Изотермы адсорбции Ленгмюра в линейных координатах
Таким образом, результаты расчетов показывают, что более высокие значения коэффициентов корреляции R2, равные 0,999 в модели Ленгмюра и самые низкие R2 0,859 в модели Темкина.
Максимальная обменная емкостьпри увеличении температуры принимает следующие значения: 298 К – 0,62 ммоль/г, 318 К – 1,04 ммоль/г и 333 К – 1,29 ммоль/г. С увеличением температуры происходит уменьшение константы kL с 95,41 до 77,3 мл/ммоль. Эта константа характеризует энергию взаимодействия ионов на поверхности твердой фазы.
Физический смысл константы адсорбции Фрейндлиха отражает относительную адсорбционную способность. Изотерма Фрейндлиха, в отличие от изотермы Ленгмюра не дает предельного насыщения. Рассчитанные значения kF увеличиваются с ростом температуры.
Определение оптимальных условий извлечения ионов тяжелых металлов необходимы сведения кинетических и термодинамических параметров. При сорбционной очистке водных объектов одним из важных технологических параметров является скорость извлечения тяжелых металлов.
Процесс адсорбции ионов кадмия при температуре 298 К протекает за 15 мин. В начальный момент (рис. 4) зависимость линейная. Скорость адсорбции рассчитывается по уравнению [6]:
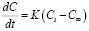 (5)
(5)
или в интегральной форме:
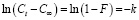 (6)
(6)
где Ct и C∞ – концентрации в момент времени (t) и после установления равновесия соответственно, ммоль/мл; F – скорость достижения равновесия; k – константа скорости реакции, c–1.
Обработка полученных данных по уравнению (6) показала, что время, при котором наблюдается прямолинейность функции ln(1 – F) = f(x), зависит от температуры. Значение константы скорости процесса сорбции (k = 6,18 ∙ 10–3, c–1) определили согласно (рис. 5).
Различия в адсорбции ионов кадмия при разных температурах позволило рассчитать термодинамические характеристики: изменение энтальпии (ΔН) и энергии Гиббса (ΔG).
Энергию Гиббса определяли по уравнению:
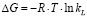 , (5)
, (5)
Расчет ΔН производили с использованием изостеры в интегральном виде:
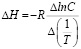 (6)
(6)
По рассчитанным значениям ΔG и ΔН определили значения ΔS из уравнения:
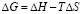 . (7)
. (7)
Результаты расчета термодинамических параметров приведены в таблице2.
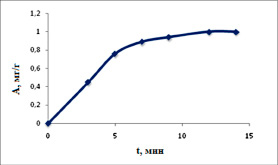
Рис. 4. Кинетическая кривая адсорбции ионов кадмия при Т=298 К
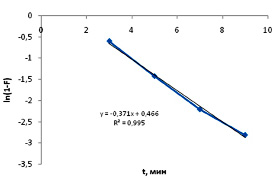
Рис.5. Зависимость ln(1–F) от времени адсорбции ионов кадмия
Таблица 2
Термодинамические параметры адсорбции кадмия
|
Температура, К |
Amax, мг/г |
ΔG, кДж/моль |
ΔН, кДж/моль |
ΔS, Дж/моль∙К |
|
298 |
0,62 |
-11,30 |
-2,23 |
45,40 |
|
318 |
1,04 |
-11,82 |
44,18 |
|
|
333 |
1,29 |
-12,04 |
42,85 |
Отрицательные значения ΔG с повышением температуры изменяются незначительно и подтверждают самопроизвольное протекание процесса адсорбции ионов кадмия [7]. Отрицательное значение ΔН для изотерм носит экзотермический характер, означающий физическую адсорбцию.
При постоянном значении емкости адсорбента взаимосвязь температур и концентраций отражают изостеры. Согласно уравнению (6) была рассчитана ΔН по углам наклона изостер. Процесс адсорбцииионов кадмия на монтмориллонитовой глине начинается с активных мест поверхности. Затем по мере заполнения поверхности принимают участие менее активные центры и ΔН принимает низкие значения, которые подтверждают физическую адсорбцию.
Заключение
Исследованы закономерности адсорбции Cd2+. Установлена максимальная емкость сорбента 0,62 ммоль/мл при температуре 298 К. Коэффициенты корреляции модели Ленгмюра (R2 = 0,999) показывают лучший результат, чем модели Фрейндлиха (R2 = 0,973) и Темкина (R2 = 0,859).
Изучены кинетические закономерности сорбции и определены термодинамические показатели. Рассчитаны значения ΔН (-2,23 кДж/моль), ΔG уменьшается с увеличением температуры. Установлено, что адсорбция при температуре 298 К протекает с высокой скоростью, при этом равновесие достигается за 15 минут.
Таким образом, полученные данные будут полезны для сорбционной очистки загрязненных вод.



